2) Найти спектр сигнала вида . Найти спектр сигнала, который получается после интегрирования сигнала , используя свойство преобразования спектров при интегрировании сигналов.

Рассмотрим сигнал, являющийся суммой двух дельта-импульсов, отстоящих один от другого на временной интервал, равный .

(2.28)

Спектр такого сигнала будет

(2.29)

График этой функции представлен на рис.2.11.

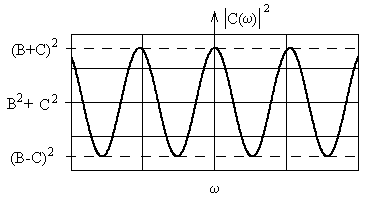
Рис.2.11

Спектральная плотность энергии меняется периодически с частотой, и это связано с интерференцией спектральных компонент от каждого дельта-импульса. На частотах =0, 2, 4 и т.д. спектральные компоненты от каждого дельта-импульса действуют синфазно, как будто мы имеем один импульс с интенсивностью В+С, а на частотах =, 3, 5 и т.д. противофазно как будто импульс имеет интенсивность В-С.

Интегрируя разность дельта-импульсов

, (2.40)

Мы получим прямоугольный сигнал (рис.2.1). Полагая в (2.29) В=А и С=-А и деля спектр на , получим спектральную плотность энергии (2.24) прямоугольного сигнала.

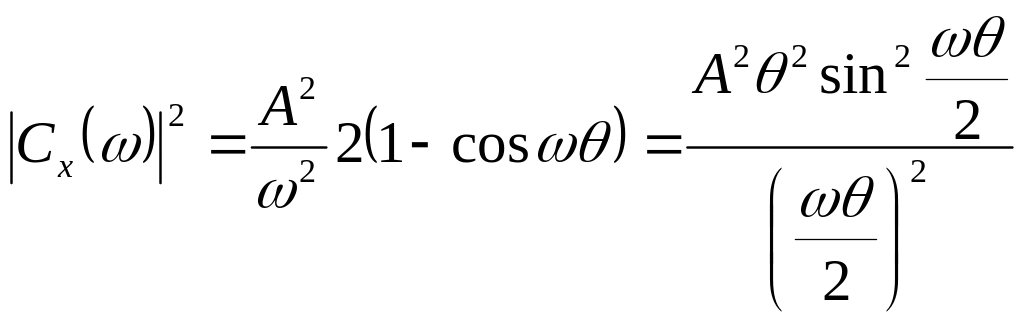
Билет 13

1) Гармонический сигнал со случайной фазой. Найти одномерную функцию плотности распределения.

Рассмотрим также гармонический сигнал со случайной фазой. Запишем этот сигнал в виде

(3.28)

График этой функции представлен на Рис.3.2. Здесь фаза сигнала обозначена как .

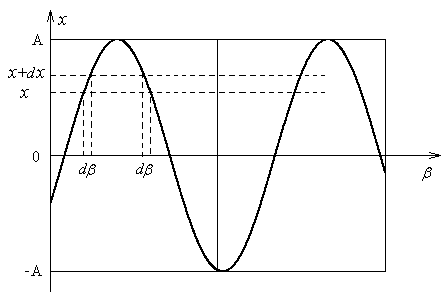
Рис.3.2

Если выделить некоторый произвольный момент времени t=t₁, то величина сигнала будет случайной, так как начальная фаза  является случайной. Ясно из рисунка, что случайная величина x заключена в интервале [-A,A] и имеет среднее значение, равное нулю.

Вероятность того, что сигнал находится в интервале между x и x +dx равна , где есть искомая функция плотности вероятности. Это событие случается, когда фазовый угол попадает в один из двух интервалов d, показанных на Рис.3.2 Вероятность такого события можно записать, как , где есть функция плотности вероятности фазы. Так как фаза равномерно распределена в интервале 2, то . Теперь можно написать, что

(3.29)

Из этой формулы легко найти функцию плотности вероятности в виде

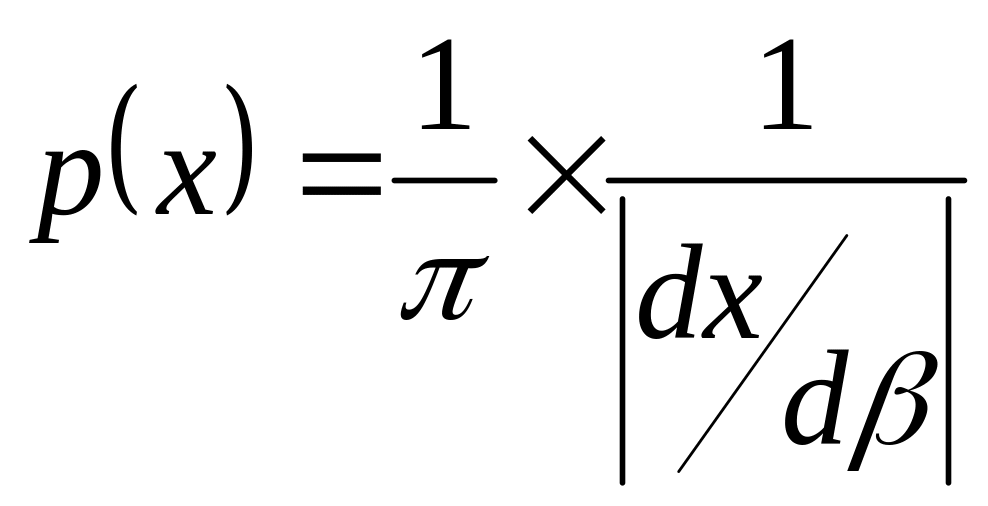(3.30)

где взято модульное значение производной , поскольку рассматриваемые случайные события не зависят от знака производной.

Учитывая, что , производную находим в виде

(3.31)

Подставляя (3.31) в (3.30), находим функцию плотности вероятности в виде

(3.32)

График этой функции в случае А=1 показан на Рис.3.3

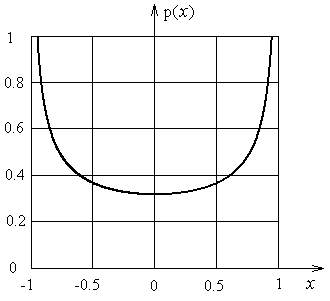
Рис.3.3

2) Вычислить спектральную плотность амплитуды и спектр энергии сигнала вида . Билет 14

1) Амплитудная модуляция, используемая в системах цифровой связи.

Цифровой АМ сигнал на интервале времени (0 t T) можно представить как:

(5.1)

где A_m (m=1,2,…,M) означает ряд из M возможных амплитуд, соответствующих возможным символам. Функция описывает форму вещественного сигнального импульса, которая определяет спектр передаваемого сигнала. Амплитуда сигнала A_m принимает дискретные значения

(5.2)

где 2d – расстояние между соседними амплитудами сигналов. Таким образом, имеем, что

Скорость передачи символов при АМ равна R/k. Это скорость, с которой происходят изменения амплитуды несущей для того, чтобы отразить новую информацию. Временной интервал называется информационным или битовым интервалом, а временной интервал называется символьным интервалом или интервалом канального символа.

Обозначим E_g - энергия импульса . Тогда сигналы АМ имеют энергию

, (5.3)

АМ сигналы являются одномерными и их можно представить в общем виде как:

(5.4)

где f(t) определен как узкополосный сигнал с единичной энергией:

, (5.5)

(5.6)

На рис. 5.1 даны диаграммы сигналов для М=2, М=4, М=8.

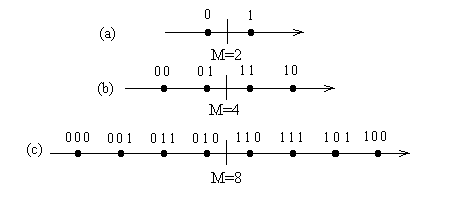
Рис. 5.1.

Отображение информационных бит амплитудами сигнала можно сделать различными способами. Наилучшим способом является такой, при котором соседние амплитуды сигналов соответствуют информационным двоичным блокам, различающимся в одном разряде, как показано на рис. 5.1. Такое отображение называется кодом Грея. Выбор кода имеет значение при демодуляции сигналов. Из-за влияния шума и помех возможен ошибочный выбор амплитуды. Наиболее вероятной является ошибка, при которой выбирается соседняя амплитуда. В случае кода Грея возникает ошибка в битовой последовательности только в одном бите.

Евклидово расстояние между какой-либо парой сигнальных точек равно

(5.7)

Следовательно, расстояние между парой соседних точек, т.е. минимальное евклидово расстояние, равно

(5.8)

Заметим, что в частном случае M=2 двоичная АМ имеет специальное свойство:

(5.9)

Эти два сигнала имеют одинаковую энергию и коэффициент их взаимной корреляции равен –1. Такие сигналы называются противоположными.