Решение методами спуска.

Рассмотрим следующую нелинейную систему уравнений:

Представим нашу задачу нахождения решения данной системы как оптимизационную, или иначе, экстремальную задачу. Из функций системы образуем новую функциюТак как эта функция неотрицательная, то найдется точкатакая, что, т.е.Следовательно, если тем или иным способом удается получить точку, минимизирующую функцию, и если при этом окажется, что, то- искомое решение системы.

Аналогично для n-мерной системе задачи сведем ее решение к экстремальной задаче

Теперь перейдем непосредственно к методам спуска. Основная идея методов спуска заключается в том, что при заданном начальном приближении определяется направление, в котором функция убывает и производится перемещение в этом направлении. Если величина шага перемещения выбрана не очень большой, то значение функции уменьшается. Алгоритм любого метода спуска задается формулой , где –k-тое приближение к решению, - некоторый вектор,- длина шага в направлении.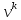

Как правило, в качестве выбирается значение, реализующее

В методе наискорейшего спуска вектор полагается равным вектору, противоположному градиенту функции F в точке и задающему направление наискорейшего убывания функции F в точке

В методе покоординатного спуска в качестве выбираются векторы, параллельные поочередно каждой из осей координат (в двумерном случае

Таким образом, задача многомерной оптимизации сводится на каждом шаге к решению задачи Одномерная оптимизация по данной формуле проводится, как правило, методом золотого сечения с учетом следующего замечания. На прямойможет существовать несколько локальных минимумов. Поскольку нас интересует ближайший, то до применения метода золотого сечения его вначале локализуют способом, аналогичным описанному в методе золотого сечения. Отличие состоит в том, что задавшись некоторым шагом, заведомо меньшим половины расстояния между двумя локальными экстремумами исследуемой функции, мы вычисляем значениядо тех пор, пока не выполнится условие. После этого вызываем процедуру метода золотого сечения, в которой минимизируется функцияпо переменнойна сегменте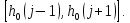

В методе покоординатного спуска неизвестно, убывает или возрастает функция в направлении . Поэтому здесь при выполнении на первом шаге условияследует изменить направление на противоположное или, что эквивалентно, изменить знаки повторить алгоритм локализации.

Приведем графическое изображение работы методов.

Метод покоординатного спуска:

Метод наискорейшего спуска:

Реализация программы.

Программа реализована на языке C# в среде Visual Studio 2008. Ниже приведены функции для решения систем каждым из методов.

Полюсный метод Ньютона.

public void newton()

{

double[] solution, newsolution;

solution = new double[n];

newsolution = new double[n];

for (int i = 0; i < n; i++)

solution[i] = Convert.ToDouble(dataXStart[0, i].Value);

double[,] Fder = new double[n, n];

double[,] A = new double[n, n];

double[,] Fa = new double[n, n];

double[,] temp = new double[n, n];

double[,] C = new double[n, n];

double[,] CmX = new double[n,n];

double[] F = new double[n];

double[] d = new double[n];

double[] tempsmall = new double[n];

for (int i = 0; i < n; i++)

{

for (int j = 0; j < n; j++)

{

C[i, j] = Convert.ToDouble(dataGridView1[j, i].Value);

}

}

bool exit = new bool();

int numiter = new int();

exit = false;

dataGridView2.ColumnCount = n;

dataGridView2.RowCount = 1;

for (int i = 0; i < n; i++)

dataGridView2.Columns[i].Width = (dataGridView2.Width - 45) / n;

while (!exit)

{

numiter++;

for (int i = 0; i < n; i++)

{

F[i] = vm.getVal(i, solution);

d[i] = vm.getVal(i, solution);

for (int j = 0; j < n; j++)

{

Fder[i, j] = vm.derVal(i, j, solution);

CmX[i,j]=C[i,j]-solution[j];

}

}

for (int anum = 0; anum < n; anum++)

{

for (int i = 0; i < n; i++)

{

for (int j = 0; j < n; j++)

{

if (j == anum)

continue;

temp[i, j] = CmX[i, j];

}

temp[i, n - 1] = d[i];

}

A[0, anum] = det.rmatrixdet(temp, n);

if (anum % 2 != 0)

A[0, anum] *= -1;

if (n % 2 != 0)

A[0, anum] *= -1;

double deter = det.rmatrixdet(CmX, n);

if (deter != 0)

A[0, anum] /= deter;

}

for (int i = 1; i < n; i++)

{

for (int j = 0; j < n; j++)

{

A[i, j] = A[0, j];

}

}

vm.clear(ref temp, n);

for (int i = 0; i < n; i++)

for (int j = 0; j < n; j++)

temp[i,j] = Fder[i, j] - A[i, j];

inv.rmatrixinverse(ref temp, n);

for (int i = 0; i < n; i++)

{

double tempd=new double();

for (int j = 0; j < n; j++)

tempd =tempd + temp[i, j] * F[j];

tempsmall[i]=tempd;

}

for (int i = 0; i < n; i++)

newsolution[i] = solution[i] - tempsmall[i];

exit = checkNewton(newsolution);

for (int i = 0; i < n; i++)

solution[i] = newsolution[i];

dataGridView2.RowCount = dataGridView2.RowCount + 1;

for (int i = 0; i < n; i++)

dataGridView2[i, numiter-1].Value = (object)solution[i];

}

label3.Text = numiter.ToString();

dataGridView2.RowCount = dataGridView2.RowCount + 1;

double neviaz = vm.getVal(0, solution);

for (int i = 1; i < n; i++)

{

if (neviaz < vm.getVal(i, solution))

neviaz = vm.getVal(i, solution);

}

dataGridView2[0, dataGridView2.RowCount - 1].Value = neviaz.ToString();

label9.Text = neviaz.ToString();

}