
- •Предмет, метод статистики, основные категории статистики.
- •Виды статистических группировок и решаемые ими задачи.
- •6.Абсолютные и относительные величины в статистике, единицы измерения.
- •7.Средние величины, виды средних. Научные основы расчета средних величин.
- •9.Структурные средние и их применение в статистике.
- •10.Понятие вариации признаков, показатели вариации. Значение и задачи изучения вариации.
- •Сокращенные способы расчета дисперсии:
- •14.Выборочное наблюдение, преимущества и недостатки.
- •15.Способы формирование выборочной совокупности.
- •16.Средняя и предельная ошибки выборки. Взаимосвязь показателей ошибки выборки с объемом выборочной совокупности и способом отбора.
- •20.Ряды динамики, их элементы и правила построения. Виды рядов динамики.
- •Правила построения рядов динамики
- •26.Понятие индекса. Виды индексов, задачи их применения.
- •27. Агрегатный индекс как основная форма общего индекса. Правила построения, анализ абсолютных приростов.
- •Агрегатная форма индекса
- •29.Индексы средних величин. Индексы постоянного состава и влияния структурных изменений на динамику средней величины.
- •31.Территориальные индексы, их значение, способы построения.
29.Индексы средних величин. Индексы постоянного состава и влияния структурных изменений на динамику средней величины.
Индексы средних величин позволяют изучать динамику средних величин. Как правило, такая потребность возникает в случаях, если:
одна и та же продукция продается по различным ценам (на различных рынках);
один и тот же вид продукции выпускается на различных предприятиях с различной себестоимостью;
на производство одного и того же вида изделий затрачивается разное время;
посевы одинаковой культуры имеют различную урожайность и т.д.
Динамика средней и факторы, ее формирующие, характеризуются с помощью системы индексов. При этом определяют:
индекс переменного состава;
индекс постоянного состава;
индекс структурных сдвигов.
Индекс переменного состава характеризует динамику средней величины и представляет собой отношение средней в отчетном периоде к средней величине базисного периода, рассчитанных по формуле средней арифметической взвешенной:
-

— основная формула индекса переменного состава.
В данном случае — цена, динамику средней которой мы ищем, в качестве веса используется объем продаж — . В том случае, если есть структура продаж товара, принимают следующую формулу:

Здесь объем продаж представлен в виде удельного веса в общем объеме.
Изменение средней величины могут вызвать два фактора:
изменение индивидуальной цены;
изменение структуры продаж.
Влияние первого фактора отражает индекс постоянного (фиксированного) состава:

Влияние второго фактора отражает индекс структурных сдвигов:
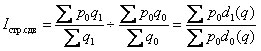
В предлагаемом ниже примере рассмотрим индекс средней себестоимости единицы продукции.
Пример расчета индексов средних величин. На предприятиях отрасли производится один вид продукции (табл. 4).
Таблица 4
Предприятие |
Себестоимость единицы продукции, у. е. |
Количество продукции, шт. |
||
цена, руб. |
кол-во |
цена, руб. |
кол-во |
|
1 |
256 |
320 |
1480 |
1500 |
2 |
250 |
315 |
2000 |
2200 |
Итого: |
— |
— |
3480 |
3700 |
Определите, как изменилась средняя себестоимость на производство единицы продукции по отрасли всего и в том числе за счет отдельных факторов.
Средние затраты рассчитаем при помощи средней арифметической взвешенной, затем найдем индекс переменного состава:

Таким образом, средняя себестоимость в целом по отрасли выросла на 25,5 %.
Динамика средней себестоимости единицы продукции в целом по отрасли складывается под влиянием двух факторов:
изменения себестоимости единицы продукции на отдельном предприятии;
структуры производства продукции отрасли.
Рассчитаем индекс фиксированного состава:

Таким образом, в результате повышения себестоимости единицы продукции на обоих предприятиях средняя себестоимость единицы продукции выросла на 25,6 %.
Определим влияние на среднюю себестоимость структурных сдвигов:

За изучаемый период структура производства практически не изменилась, поэтому изменение средней цены произошло целиком за счет влияния первого фактора, то есть изменения себестоимости на производство продукции на каждом предприятии.
Правильность расчетов подтверждает проверка через взаимосвязь индексов.
![]()
