
- •Основная теорема зацепления Виллиса
- •11. Какие стандартные значения могут принимать коэффициенты и ?
- •Эвoльвента. Уравнение Эвальвенты. Параметры и свойства.
- •Связь между эвольвентой и образующей прямой
- •8. Доказать, что эвольвентная передача имеет малую чувствительность к неточности монтажа передач
- •7. Эвольвентное зацепление. Параметры и свойсва.
- •8. 9. Эвольвентное зубчатое колесо. Параметры.
- •10. Рейка. Параметры.
- •11. 12. Способы изготовления зубчатых колес
- •13. Эвольвентное зубчатое зацепление. Параметры
- •14. Станочное зацепление. Параметры
- •15. Классификация зубчатых колес
- •16. Вывести формулу, связывающую коэффициент изменения толщины зуба по делительной окружности с коэффициентом смещения реечного инструмента
- •17. Влияние коэффициента смещения на форму зуба
- •39. Как графически определить контактирующие точки в эвольвентном зубчатом зацеплении
- •40. Как экспериментально определить шаг по основной окружности и модуль
- •41. Классификация зубчатых передач. Воспринимаемое смещение.
- •43.Качественные показатели передач.
- •44.Что такое дуга зацепления? Указать на чертеже.
- •45. Передаточные отношения рядового ступенчатого редуктора
- •46. Дать основные схемы планетарных редукторов
- •47. Графический метод определения передаточного отношения планетарного редуктора
- •48. Вывод формулы Виллиса для определения передаточного отношения планетарного редуктора
- •49. Метод обращенного движения. Пример применения.
- •50. Условие соседства и соосности планетарных редукторов (сущность и вывод формулы)
- •51. Условие сборки многосателлитных планетарных редукторов (сущность и вывод формулы)
- •52. Что называется дифференциальным механизмом? Начертить схему.
- •53. Сравнительная оценка планетарных и рядовых редукторов
- •Планетарные передачи
15. Классификация зубчатых колес
 – нулевое
колесо; S>U
– положительное колесо =>
– нулевое
колесо; S>U
– положительное колесо =>
 ;
S<U
– отрицательное колесо =>
;
S<U
– отрицательное колесо =>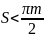 ;
;
 ,
где △
– коэффициент изменения толщины зуба
по делительной окружности. Если △=0,
то колесо нулевое, если △>0
– положительное, если △<0
– отрицательно.
,
где △
– коэффициент изменения толщины зуба
по делительной окружности. Если △=0,
то колесо нулевое, если △>0
– положительное, если △<0
– отрицательно.
16. Вывести формулу, связывающую коэффициент изменения толщины зуба по делительной окружности с коэффициентом смещения реечного инструмента
Вывод формулы для толщины зуба по произвольной окружности:
 ;
;
 ;
->
;
->
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;

17. Влияние коэффициента смещения на форму зуба
 (1)
(1)
При
увеличении коэффициента смещения x
толщина зуба
 будет уменьшаться вследствие быстрого,
прогрессирующего роста
будет уменьшаться вследствие быстрого,
прогрессирующего роста
 .
При некотором критическом значении
.
При некотором критическом значении
 наступает заострение зуба:
=0.
Опасность заострения особенно велика
у колёс с малым числом зубьев (менее
17). Для предотвращения излома вершины
заостренного зуба коэффициент смещения
x
ограничивают верхним значением
наступает заострение зуба:
=0.
Опасность заострения особенно велика
у колёс с малым числом зубьев (менее
17). Для предотвращения излома вершины
заостренного зуба коэффициент смещения
x
ограничивают верхним значением
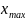 так, чтобы толщина зуба
,
подсчитанная по уравнению (1), была не
менее 0,2m,
т.е.
так, чтобы толщина зуба
,
подсчитанная по уравнению (1), была не
менее 0,2m,
т.е.
 .
Указанная зависимость формы зубьев от
коэффициента смещения x
резко ощутима при малых числах зубьев
и ослабляется по мере увеличения их
числа.
.
Указанная зависимость формы зубьев от
коэффициента смещения x
резко ощутима при малых числах зубьев
и ослабляется по мере увеличения их
числа.
18. Как по внешнему виду определить тип колеса: (+), (-), (0)
В зависимости от установки рейки относительно заготовки можно получить три варианта нарезания колеса – нулевое, положительное и отрицательное колеса.

Рисунок 1 – Рисунок 2 - Рисунок 3 –
Нулевое колесо Положительное колесо Отрицательное колесо
Обозначим: N – делительная прямая рейки (по этой прямой толщина зуба и ширина впадины на рейке одинаковы),W – начальная прямая рейки (эта прямая рейки при нарезании перекатывается вместе с рейкой по делительной окружности нарезаемого колеса), d – диаметр делительной окружности, х – коэффициент смещения, е = xm – смещение инструмента.
При нарезании нулевого колеса делительная прямая N рейки совпадает с начальной прямой W (рисунок 1).Толщина зуба по делительной окружности нулевого колеса равна ширине впадины.
При нарезании положительного колеса делительная прямая N рейки смещена от начальной прямой W на расстояние е от центра заготовки (рисунок 2).Толщина зуба по делительной окружности положительного колеса больше ширины впадины.
При нарезании отрицательного колеса делительная прямая N рейки смещена от начальной прямой W на расстояние е к центру заготовки (рисунок 3).Толщина зуба по делительной окружности отрицательного колеса меньше ширины впадины.
19. Определить графически скорость относительного скольжения эвольвентных профилей
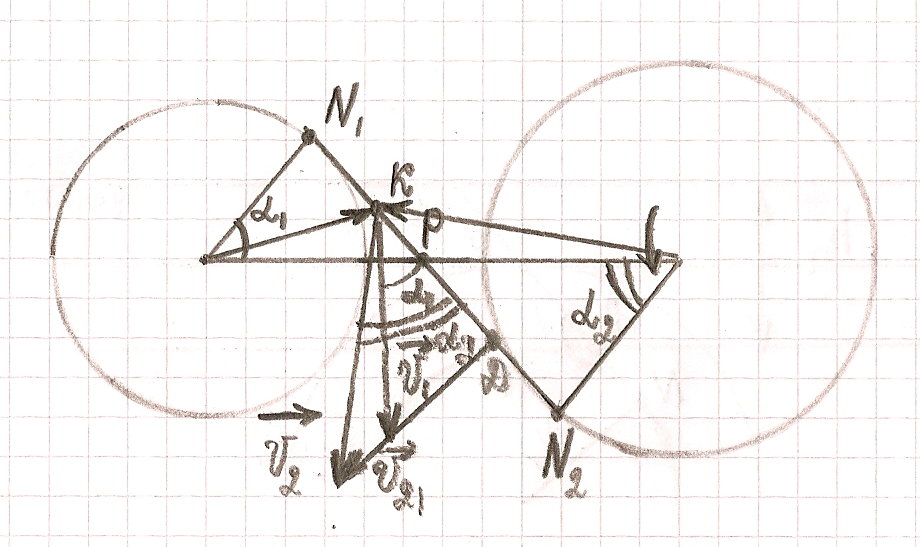
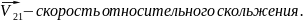 При
графическом определении этой скорости
нормальные составляющие скоростей
При
графическом определении этой скорости
нормальные составляющие скоростей
 одинаковы, а
одинаковы, а
 могут
быть разными.
могут
быть разными.




 =
=

20. Подрез зуба. Когда он возникает?
П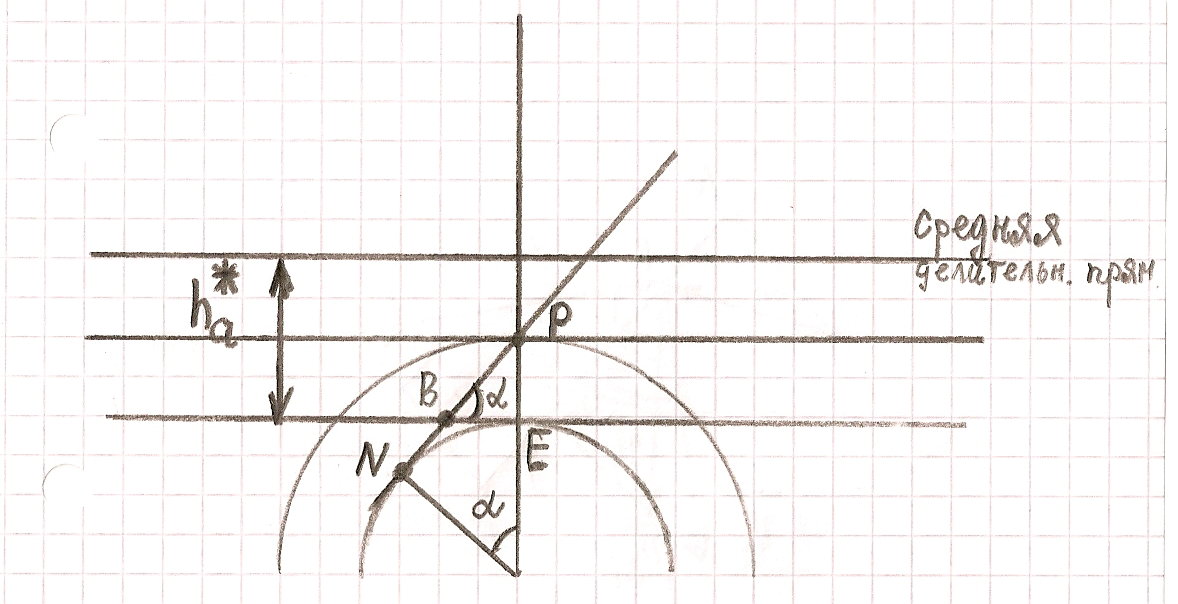 одрез
– утончение на ножке зуба
одрез
– утончение на ножке зуба



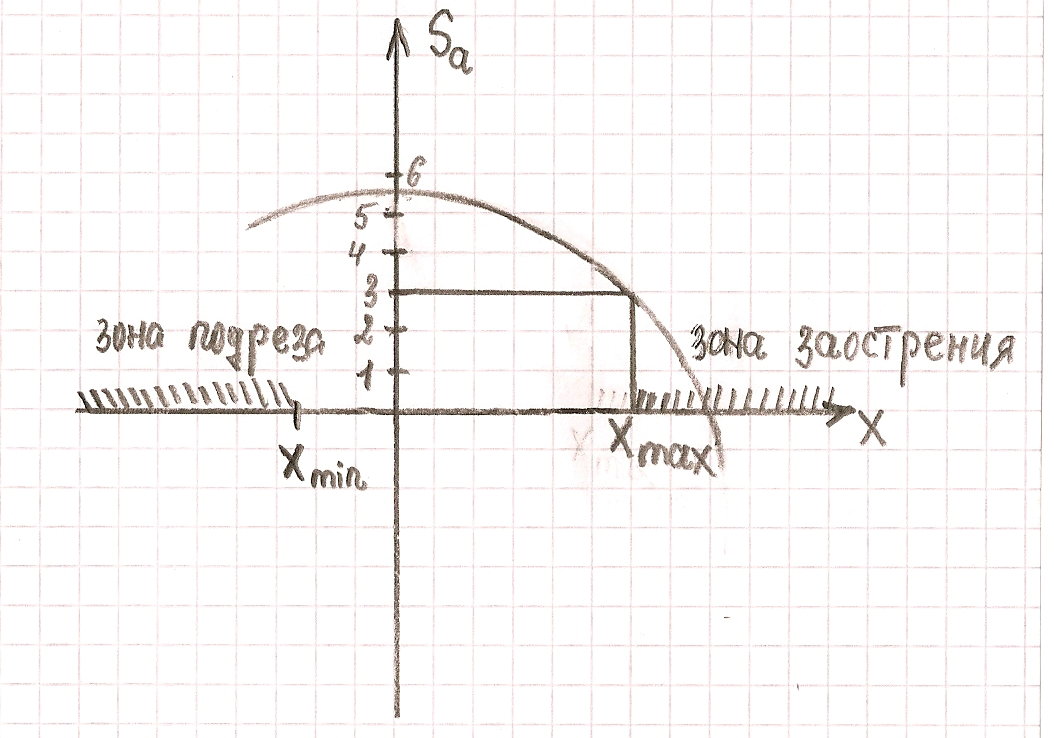


Определим число зубьев, которое можно нарезать без подреза, не смещая реечный инструмент:
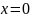
 ;
;
 ;
;

21. Заострение зуба. Дать условие отсутствия заострения.
Заострение – утоньшение на вершине зуба. Зуб считается заострённым, если его толщина
Sa ≤ 0,2m

22. Дать определение делительной окружности
Делительная окружность (r) – окружность стандартного модуля, стандартного шага и стандартного угла давления (стандартный угол давления α=20о).
23. По каким условиям определяется наименьший и наибольший коэффициент сдвига режущего инструмента?
Для предотвращения излома вершины заостренного зуба коэффициент смещения x ограничивают верхним значением x_max так, чтобы толщина зуба s, была не менее 0,2m, т.е. s≥0,2m.
Для предотвращения подреза коэффициент смещения x должен быть больше величины x_min, которая определяется по формуле
,
где

25. Какие исходные данные необходимо иметь, чтобы нарезать зубчатое колесо?
Параметры режущего инструмента(4): , c*, m, угол α; число зубьев; коэффициент смещения x. (итого 6)
24. Дать связь между делительной и основной окружностями.
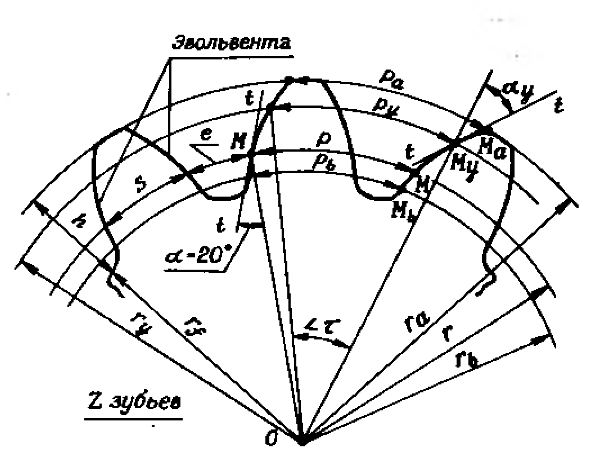
r=rb/cosα, где r – радиус делительной окружности, rb – радиус основной окружности
26. Классификация передач. Воспринимаемое смещение.
В
зависимости от
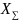 (икс
суммарного)
(икс
суммарного)
Положительная ( >0)
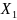 >0,
>0,
 >0
>0,
=0
>0
>0,
=0
>0,
<0,
 >
>

inv
 > inv α
> inv αcos < cos α ->
 > 1 ,
>
> 1 ,
>
 =
=
 +
+

y > 0
Отрицательная( <0)
<0, <0 <0, =0
|<0, >0, >
inv < inv α
< α = 20º
cos > cos α -> > 1
< = +
y < 0
Нулевая( 0)
0)
= =0 – нулевая нормальная
= - – нулевая равносмещенная
= α = 20º
=
;

Воспринимаемое смещение - расстояние между делительными окружностями.
27.
Дать схему станочного зацепления при
нарезании положительного, нулевого и
отрицательного колеса.

Если есть расстояние между делительной прямой и делительной окружностью – колесо положительное, нет – нулевое, если они пересекаются – отрицательное.
28.Что такое шаг? Что такое модуль?
Модуль – часть диаметра, приходящаяся на 1 зуб
Шаг — расстояние между одноименными точками двух соседних профилей зубьев, измеренные по дуге соответствующей окружности. Если по делительной окружности – то он стандартный.
29. Какое наименьшее число зубьев может быть нарезано рейкой без подреза и без сдвига реечного инструмента?

Если
=1
и α=20ᵒ, то



30.При нарезании колеса со смещением чему равно уравнительное смещение? Показать на схеме.
Уравнительное
смещение-y*m.
Вводится для того, чтобы в отсутствии
бокового зазора мы имели стандартный
радиальный зазор.
aw=r1+r2+y*m=ra1+rf2+c*m

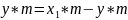 +
+

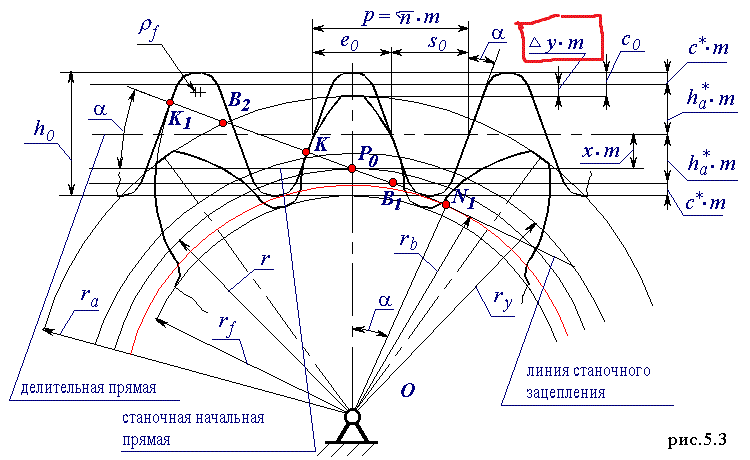
31. Когда уравнительное смещение равно нулю?
Уравнительное смещение равно нулю, когда начальная окружность совпадает с делительной.
32.Какие параметры зубчатого колеса зависят, а какие не зависят от коэффициента реечного смещения x.
Зависят: толщина зуба(Sa), Не зависят: число зубьев(z), модуль(m), шаг зубьев(Р), радиусы окружностей вершин, впадин, основной и делительной окружностей(ra , rf , rb ,r), высота зуба(Н)
 33.
Как графически определить рабочую часть
боковой поверхности зуба?
33.
Как графически определить рабочую часть
боковой поверхности зуба?
34. Когда возникает необходимость сдвига режущего инструмента?
1.
Когда z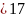
2. Когда колесо толстое или маленькое.
36. Основные формулы эвольвентного зубчатого зацепления.
Pw=Sw1+Sw2;
invw=inw+ *2tg
aw=
*2tg
aw= ;
;
y=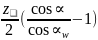 ;
;
y=x-y
35. Определить графически теоретическую линию зацепления, выделить на ней ее практическую часть.
N1N2-теоретическая линия зацепления; В1В2-практическая часть линии зацепления;
r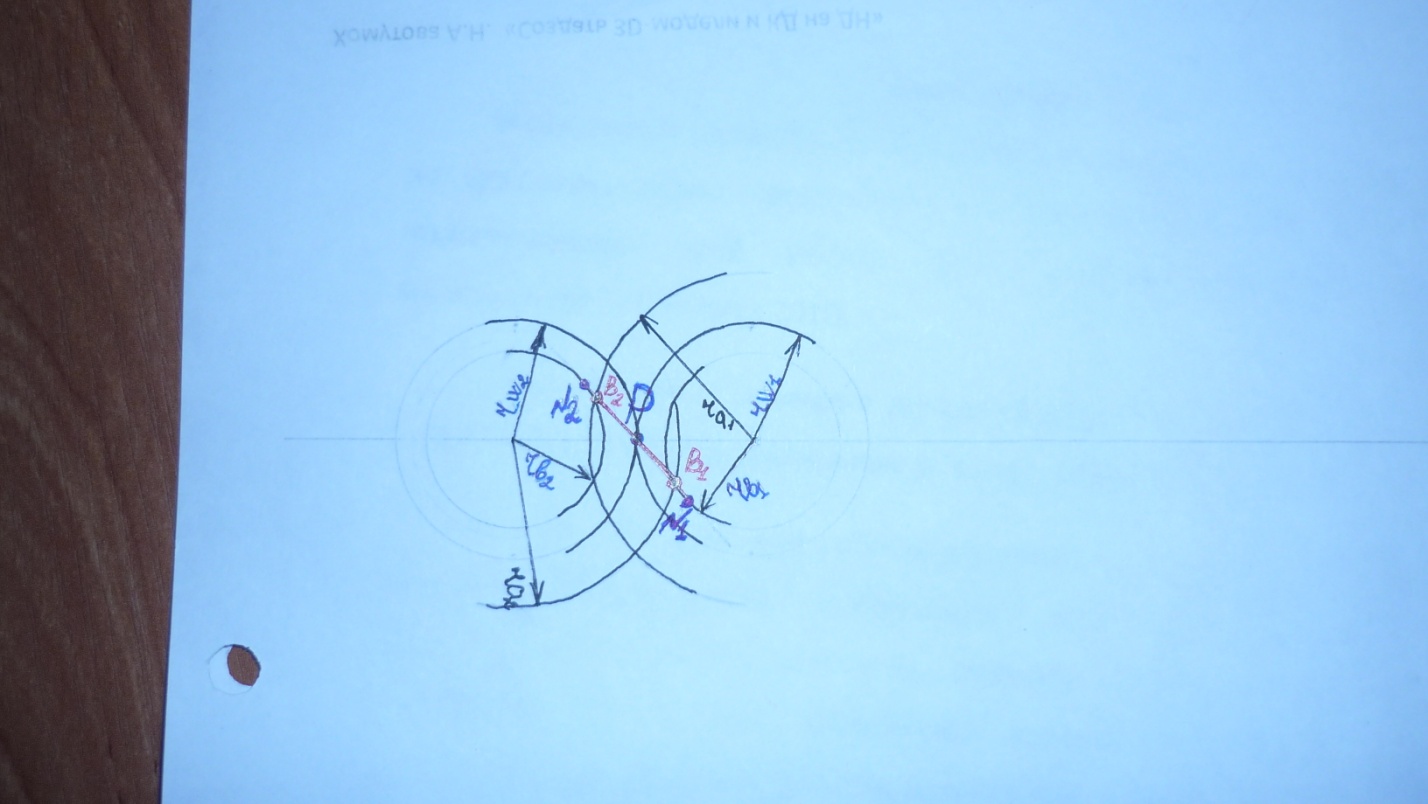 w-
радиус начальной окружности, rb-радиус
основной окружности, ra-радиус
окружности вершин
w-
радиус начальной окружности, rb-радиус
основной окружности, ra-радиус
окружности вершин
37. Размеры зубчатого колеса
Диаметр вершин прямозубого колеса
da=2ra=m(z+2 +2x-2∆y)
Диаметр впадин прямозубого колеса
df= da-2h
высота зуба
h = m(2 +c*-∆y)
Если x=0 (смещения инструмента нет) и ∆y, то da=m(z+2 ), h = m(2 +c*) и при стандартных значениях =1,0 и c*=0,25 получим da=m(z+2) и h =2,25m
Толщина зуба s
s=πm/2 + 2xm*tgα
Если инструмент установлен относительно колеса без смещения (xm=0), то s=πm/2, значит, толщина зуба s по делительной окружности колеса равна ширине впадины e, так как s+e= πm. В этом случае получается колесо с равноделенным шагом s=e. Если xm>0, то s> πm/2 и следовательно, s>e. Если xm<0, то s< πm/2, и поэтому s<e.
 38.
Доказать, что дуга зацепления по основной
окружности равна практической линии
зацепления B1B2
=
∪
Tb
38.
Доказать, что дуга зацепления по основной
окружности равна практической линии
зацепления B1B2
=
∪
Tb
∪ М1N1= NB1; ∪ М2N1= NB2; ∪ Tb=M1M2=B1B2
