Итерация прямого хода алгоритма Гаусса

На рисунке представлена общая схема состояния данных на i-й итерации прямого хода алгоритма Гаусса. Все коэффициенты при неизвестных, расположенные ниже главной диагонали и левее столбца i, уже являются нулевыми. На i-й итерации прямого хода метода Гаусса осуществляется обнуление коэффициентов столбца i, расположенных ниже главной диагонали, путем вычитания строки i, умноженной на величину / , соответствующую k-й строке. После n-1–й итерации матрица приводится к верхнему треугольному виду.

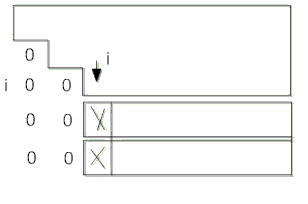
Рис. 9

Строка, которая используется для исключения неизвестных в прямом ходе метода Гаусса, называется ведущей, а диагональный элемент ведущей строки – ведущим элементом. Вычисление невозможно, если ведущий элемент равен нулю. Даже если ведущий элемент отличен от нуля, но имеет малое значение, деление на этот элемент может приводить к накоплению вычислительной погрешности и вычислительной неустойчивости алгоритма.

Для того чтобы избежать этой проблемы, на каждой итерации прямого хода в столбце, соответствующем исключаемой неизвестной, определяют коэффициент с максимальным значением по абсолютной величине: y= max | |, i≤k≤n–1, а в качестве ведущей принимают строку, в которой располагается этот коэффициент (метод главных элементов).

Вычислительная сложность прямого хода алгоритма Гаусса с выбором ведущей строки имеет порядок O( ).

После приведения системы к верхнему треугольному виду из последнего уравнения преобразованной системы может быть вычислено значение переменной , после этого из предпоследнего уравнения становится возможным определение переменной = и т.д. В общем виде вычисления, выполняемые при обратном ходе метода Гаусса, представляются следующим образом:

i=n-2, n-3,….,0

Продолжим рассмотрение приведенного выше примера. Из последнего уравнения нетрудно видеть, что неизвестная =9/3=3. Подставляя это значение во второе уравнение, определим значение неизвестной =16–3=13. На последней итерации обратного хода метода Гаусса определяется значение неизвестной = 1–3∙13–2∙3 = –44. Заметим, что в обратном ходе исключение переменной, после того как она определена, может выполняться одновременно, т.е. параллельно, во всех уравнениях системы.

Определим вычислительную сложность метода Гаусса. В прямом ходе алгоритма для выбора ведущей строки на каждой итерации должно быть определено максимальное значение в столбце с исключаемой неизвестной. По мере исключения неизвестных количество строк и элементов в строках сокращается. Текущее число элементов строки (включая правую часть), с которыми производятся действия сложения и вычитания (первый элемент без вычислений полагается равным нулю), равно (n-i), где i, 0≤ i<n-2 – номер итерации прямого хода. Поскольку кроме выполнения двух операций (умножения и вычитания) с каждым элементом строки предварительно должен быть вычислен масштабирующий коэффициент / , общие затраты на выполнение действий в одной строке составят 2(n-i)+1 операций.

С учетом того, что на каждой i-й итерации, 0≤ i<n-2 (итерациям для удобства присваиваем номера от n-2 до 0) необходимо произвести n-i-1 умножений, столько же вычитаний, а также одно деление для определения очередной неизвестной. Следовательно, общая вычислительная сложность обратного хода составит:

Суммируя затраты на реализацию прямого и обратного хода, получаем:

В последнем равенстве пределы и порядок суммирования изменены с учетом замены j=n-i.

Используя элементарные формулы суммирования, в частности, известное равенство

,

получаем следующее соотношение для оценки вычислительной сложности метода Гаусса при его реализации в виде последовательного алгоритма:

T=

При большом n можно приближенно положить T≈

Вычислительная сложность обратного хода алгоритма Гаусса имеет порядок O( ). Общая сложность всего алгоритма O( ).