ДК МСС
.docxМИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«сЕВЕРО-КАВКАЗСКИЙ государственный технический университет»
Кафедра машиностроения и технологий.

 Домашняя
контрольная работа
Домашняя
контрольная работа
По теме: «Обработка результатов многократных измерений» Вариант 1
Выполнил: студент гр. ИСТБ-111
Уткин А.С.
Проверила: Владыкина Юлия Анатольевна
Ставрополь 2012
Оглавление
1.Введение 3
2.Расчетно-графическая работа 3
3.Список используемой литературы: 19
1.Введение
В данной работе необходимо определить закон распределения вероятностей результата измерения по исходным данным. Расчетно-графическая работа включает в себя расчетно-пояснительную записку.
2.Расчетно-графическая работа
Выборка результатов измерений соответствующей варианту: 5,7,7,9,9,4,5,8,6,8,10,6,11,12,10,10,17,15,13,12.
(17-4)/5=2,6

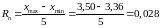 .
.
Занесем данные в таблицу 1.
Таблица 1 – Результаты наблюдений
х |
4-6,6 |
6,6-9,2 |
9,2-11,8 |
11,8-14,4 |
14,4-17 |
Середина интервала |
5,3 |
7,9 |
10,5 |
13,1 |
15,7 |
Частота
|
5 |
6 |
4 |
3 |
2 |
Вычислим оценки
 и
и
 :
:
14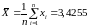 ;
;
6,08
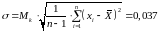 ,
,
где
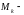 коэффициент смещения (таблица 2).
коэффициент смещения (таблица 2).
Для графического определения вида закона распределения построим гистограмму. При построении разбиение на интервалы осуществляется таким образом, чтобы измеренные значения оказались серединами интервалов.
Таблица 2 – Значения
коэффициента
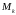 в зависимости
от количества наблюдений n
в зависимости
от количества наблюдений n
n |
Mk |
n |
Mk |
n |
Mk |
1 |
1,253 |
10 |
1,025 |
19 |
1,013 |
2 |
1,128 |
11 |
1,023 |
20 |
1,012 |
3 |
1,085 |
12 |
1,021 |
25 |
1,010 |
4 |
1,064 |
13 |
1,019 |
30 |
1,008 |
5 |
1,051 |
14 |
1,018 |
35 |
1,007 |
6 |
1,042 |
15 |
1,017 |
40 |
1,006 |
7 |
1,036 |
16 |
1,016 |
45 |
1,006 |
8 |
1,032 |
17 |
1,015 |
50 |
1,005 |
9 |
1,028 |
18 |
1,014 |
60 |
1,004 |
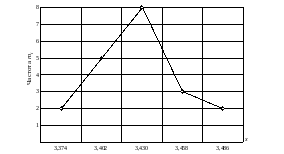
Рисунок 1 – Гистограмма
По виду гистограммы предположительно идентифицируем опытное распределение нормальным.
Определим, содержит ли результат наблюдения х=17 грубую погрешность.
3*6,08=18,24 33
17-14=3 33
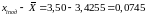 .
.
3<18.24
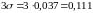 .
.
Так как, то можно сделать вывод, что результат x=17 не содержит грубой погрешности.
2. Проверка по
критерию Смирнова
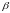 .
Из таблицы 3 для принятого уровня
значимости q
=0,05 и объема
выборки n=20
найдем
.
Из таблицы 3 для принятого уровня
значимости q
=0,05 и объема
выборки n=20
найдем
 .
Наличие грубой погрешности в результате
х=17
не подтверждается, т. к.:
.
Наличие грубой погрешности в результате
х=17
не подтверждается, т. к.:
(xi-xcp)
3<17.01(β*σ) 33
Таблица 3 – Квантили распределения βk
Объем выборки
|
Предельное значение βk при уровне значимости q |
||||
0,100 |
0,050 |
0,0010 |
0,005 |
0,001 |
|
1 |
1,282 |
1,645 |
2,326 |
2,576 |
3,090 |
2 |
1,632 |
1,955 |
2,575 |
2,807 |
3,290 |
3 |
1,818 |
2,121 |
2,712 |
2,935 |
3,403 |
4 |
1,943 |
2,234 |
2,806 |
3,023 |
3,481 |
5 |
2,036 |
2,319 |
2,877 |
3,090 |
3,540 |
6 |
2,111 |
2,386 |
2,934 |
3,143 |
3,588 |
7 |
2,172 |
2,442 |
2,981 |
3,188 |
3,628 |
8 |
2,224 |
2,490 |
3,022 |
3,227 |
3,662 |
9 |
2,269 |
2,531 |
3,057 |
3,260 |
3,692 |
10 |
2,309 |
2,568 |
3,089 |
3,290 |
3,719 |
15 |
2,457 |
2,705 |
3,207 |
3,402 |
3,820 |
20 |
2,559 |
2,799 |
3,289 |
3,480 |
3,890 |
25 |
2,635 |
2,870 |
3,351 |
3,539 |
3,944 |
30 |
2,696 |
2,928 |
3,402 |
3,587 |
3,988 |
40 |
2,792 |
3,015 |
3,480 |
3,662 |
4,054 |
50 |
2,860 |
3,082 |
3,541 |
3,716 |
4,108 |
100 |
3,076 |
3,285 |
3,723 |
3,892 |
4,263 |
250 |
3,339 |
3,534 |
3,946 |
3,946 |
4,465 |
500 |
3,528 |
3,703 |
4,108 |
4,263 |
4,607 |
3. Проверка по
критерию Романовского. Определяем
характеристики распределения без учета
подозрительного результата (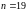 ):
):
(xi-xcp)
3<12.72(t*σ)
 и доверительной вероятности P
= 0,95;
и доверительной вероятности P
= 0,95;
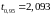 .
Наличие грубой погрешности подтверждается,
т. к.:
.
Наличие грубой погрешности подтверждается,
т. к.:
.
Таблица
4 –
Критерий
Стьюдента
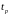 (квантили
Стьюдента)
(квантили
Стьюдента)
Довери- тельная вероят- ность Р |
Число степеней свободы k |
|||||||||||||
3 |
4 |
5 |
6 |
8 |
10 |
12 |
18 |
22 |
30 |
40 |
60 |
120 |
|
|
0,90 |
2,35 |
2,13 |
2,01 |
1,94 |
1,86 |
1,81 |
1,78 |
1,73 |
1,72 |
1,70 |
1,68 |
1,67 |
1,66 |
1,64 |
0,95 |
3,18 |
2,78 |
2,57 |
2,45 |
2,31 |
2,23 |
2,18 |
2,10 |
2,07 |
2,04 |
2,02 |
2,00 |
1,98 |
1,96 |
0,99 |
5,84 |
4,60 |
4,03 |
3,71 |
3,36 |
3,17 |
3,06 |
2,98 |
2,82 |
2,75 |
2,70 |
2,86 |
2,62 |
2,58 |
4. Проверка по критерию Шовене. При нахождении характеристик распределения участвуют все наблюдения. Вычисляем квантиль z по формуле:
(17-14)/6.08=0.493
 .
.
По таблице значений
функции Лапласа [1] определяем вероятность
выхода результатов за квантиль
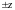 :
:
(0.493*6.08<|xi-xcp|)=P(2.99744)=0.99721
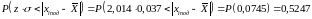 .
.
(0.493*6.08<|xi-xcp|)=20*0.99721=19.9442 Ом:
Ом:
 .
.
Так как
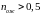 ,
то приходим к выводу об отсутствии
грубой погрешности в результате
наблюдения .
,
то приходим к выводу об отсутствии
грубой погрешности в результате
наблюдения .
5. Проверка по критерию Ирвина. Для полученных экспериментальных данных определяют коэффициент по формуле:
 .
.
Затем этот
коэффициент сравним с табличным значением
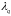 ,
значения которого приведены в таблице
5. Т. к. λ=1.15<1.3=λq,
то нулевая гипотеза не подтверждается,
т. е. результат x=17
не содержит грубой погрешности.
,
значения которого приведены в таблице
5. Т. к. λ=1.15<1.3=λq,
то нулевая гипотеза не подтверждается,
т. е. результат x=17
не содержит грубой погрешности.
Таблица 5 – Критерий Ирвина
Число измерений n |
Уровень значимости |
|
|
|
|
2 |
2,8 |
3,7 |
3 |
2,2 |
2,9 |
10 |
1,5 |
2,0 |
20 |
1,3 |
1,8 |
30 |
1,2 |
1,7 |
50 |
1,1 |
1,6 |
12-5=7
 :
:
 .
.
Выполним проверку по следующему неравенству:
 , (1)
, (1)
где
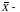 выборочное
среднее арифметическое значение,
вычисленное после исключения
предполагаемого промаха (для Xcp=14,
);
выборочное
среднее арифметическое значение,
вычисленное после исключения
предполагаемого промаха (для Xcp=14,
);
 критериальное
значение (таблица 6).
критериальное
значение (таблица 6).
Таблица 6 – Критерий вариационного размаха
|
5 |
6 |
7 |
8 –9 |
10 –11 |
12 – 15 |
16 – 22 |
23 – 25 |
26 – 63 |
|
|
1,7 |
1,6 |
1,5 |
1,4 |
1,3 |
1,2 |
1,1 |
1,0 |
0,9 |
|
6.3<17<21.7
Неравенство 1
выполняется:
 .
.
Таким образом, результат x=17 не содержит грубой погрешности.
7. Проверка по критерию Диксона. При использовании критерия вычисляют коэффициент Диксона (наблюдаемое значение критерия) для проверки наибольшего или наименьшего экстремального значения в зависимости от числа измерений. В таблице 7 приведены формулы для вычисления коэффициентов.
(12-15)/(12-7)=-0.6
 .
.
Таблица 7 – Формулы коэффициентов Диксона
Объем выборки |
Коэффициент Диксона |
Для наименьшего экстремального значения параметра |
Для наибольшего экспериментального параметра |
3 – 7 |
|
|
|
8 – 10 |
|
|
|
11 – 13 |
|
|
|
14 – 25 |
|
|
|
Таблица 8 – Критериальные значения коэффициентов Диксона (при принятом уровне значимости q)
Коэффициент Диксона |
Число измерений |
|
|||
0,1 |
0,05 |
0,02 |
0,01 |
||
|
3 4 5 6 7 |
0,886 0,679 0,557 0,482 0,434 |
0,941 0,765 0,642 0,560 0,507 |
0,976 0,846 0,729 0,644 0,586 |
0,988 0,899 0,780 0,698 0,637 |
|
8 9 10 |
0,479 0,441 0,409 |
0,554 0,512 0,477 |
0,631 0,587 0,551 |
0,683 0,636 0,597 |
|
11 12 13 |
0,517 0,490 0,467 |
0,576 0,546 0,521 |
0,538 0,605 0,578 |
0,679 0,642 0,615 |
|
14 15 16 17 18 19 20 21 22 23 24 25 |
0,462 0,472 0,452 0,438 0,424 0,412 0,401 0,391 0,382 0,374 0,367 0,360 |
0,546 0,525 0,507 0,490 0,475 0,462 0,450 0,440 0,430 0,421 0,413 0,406 |
0,602 0,579 0,559 0,542 0,527 0,514 0,502 0,491 0,481 0,472 0,464 0,457 |
0,641 0,616 0,595 0,577 0,561 0,547 0,535 0,524 0,514 0,505 0,497 0,489 |
Вычисленные для
выборки по формулам значения коэффициентов
Диксона
 сравним с
табличным значением критерия Диксона
сравним с
табличным значением критерия Диксона
 (таблица 8).
Нулевая гипотеза об отсутствии грубой
погрешности выполняется, если выполняется
неравенство
(таблица 8).
Нулевая гипотеза об отсутствии грубой
погрешности выполняется, если выполняется
неравенство
 .
.
Если
 ,
то результат признается грубой
погрешностью и исключается из дальнейшей
обработки. В нашем случае:r=-0.6<0.45=rq,
т.е. грубая погрешность отсутствует.
,
то результат признается грубой
погрешностью и исключается из дальнейшей
обработки. В нашем случае:r=-0.6<0.45=rq,
т.е. грубая погрешность отсутствует.
Поскольку все критерии (7 из 7) показали отсутствие грубой погрешности, то результат наблюдения можно оставить в выборке.
Исключение систематических погрешностей измерений.
Если приведенные результаты представить графически, то можно увидеть на графике прогрессирующую, линейно возрастающую по модулю погрешность. График показан на рисунке 2.

Рисунок 2 – График результатов
Модуль переменной составляющей систематической погрешности определим по формуле:
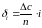 , (2)
, (2)
где
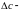 разность
между наибольшими и наименьшими
значениями результатов наблюдений (по
аппроксимирующей прямой);
разность
между наибольшими и наименьшими
значениями результатов наблюдений (по
аппроксимирующей прямой);
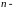 общее
число результатов;
общее
число результатов;
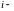 порядковый
номер измерения.
порядковый
номер измерения.
 Разность
Разность
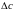 определяется
по аппроксимирующей прямой.
определяется
по аппроксимирующей прямой.
(13/20)*i=0.65*i
 .
.
Округлив значение
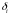 до сотых долей (точность получения
результатов)
и исключим из результатов измерений,
т. е.:
до сотых долей (точность получения
результатов)
и исключим из результатов измерений,
т. е.:
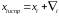 , (3)
, (3)
где
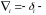 поправка, вносимая в каждый результат.
поправка, вносимая в каждый результат.
Как видно, поправка представляет собой погрешность, взятую с обратным знаком.
Систематическая погрешность, определенная по формуле 2 примет значения:
0.65 |
1.3 |
1.95 |
2.6 |
3.25 |
3.9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|

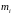

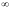
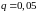


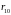

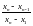

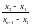
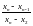

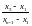
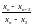

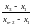
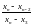
 при уровне значимости
при уровне значимости