Задача 9.

Реактивная мощность, потребляемая асинхронным двигателем (АД) при степени загрузки K_нг , определяемая зависимостью:

Q_ад = Q_xx + (Q_н –Q_xx )K

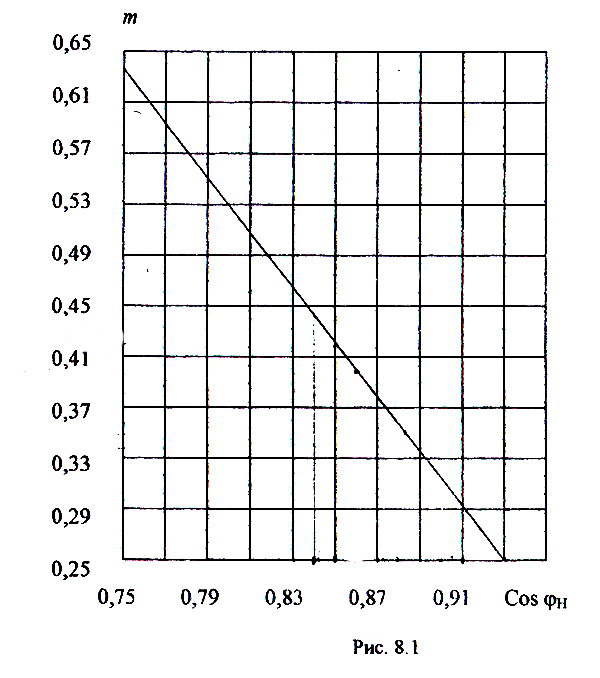
где Q_xx– реактивная мощность холостого хода АД, равная Q_xx = (Р_н/ )·m,

а m– расчетный коэффициент, зависящий от номинального коэффициента мощности cos (рис 8.

Q_н – реактивная мощность АД при номинальной нагрузке,

Q_н = (Р_н/ ) tg

Cсуммарная реактивная мощность, подлежащая компенсации при работе двух АД.

Q_к = Q_AД1+Q_АД2

Величины емкости С батареи конденсаторов, включаемых в одну фазу, при условии соединении их в треугольник

С = Q_cф10⁶/314 U , мкФ

При условии полной компенсации реактивной мощности снижение потерь мощности в питающих проводах

% =

где P-реальная активная мощность обоих АД, равная

P =

Пример

Uд,В	,кВт		cos		Pн2, кВт		сos
380	18,5	0,6	0,88	0,9	30	0,8	0,89	0,91

Решение

1.Номинальная реактивная мощность, потребляемая АД₁

Q_н1 = (Р_н1/ _н1) tg = (18,5/0,9)0,53=11,1 квар

2. Реактивная мощность АД₁ при коэффициенте нагрузки =0,6

Q_0.6=Q_xx1 + (Q_н1 – Q_xx1)

где, Q_xx1 = (Р_н1/ _н1)m=(18,5/0,9)0,35=7,19 квар,

m=0,35 находится из графика (рис 8.1)

Q_ад1=Q = Q_xx1 + (Q_н1 –Q_xx1 )K =7,19+(11,1 – 7,19)0,6²= 8,6 квар

3. Номинальная реактивная мощность, потребляемая АД₂

Q_н2 = (Р_н2/ _н2) tg = (30/0,91)0,51=16,89 квар

4. Реактивная мощность АД₂ при коэффициенте нагрузки =0,8

Q_ад2=Q_xx2 + (Q_н2 – Q_xx2)

где, Q_xx2 = (Р_н2/ _н2)m=(30/0,91)0,33=10,88 квар,

Q_ад2=Q =10,88+(16,89 – 10,88)0,64= 14,73 квар

5. Реактивная мощность, подлежащая компенсации

Q_к = Q_AД1+Q_АД2=8,6+14,73=23,32 квар

6. Величина емкости батареи конденсаторов, включенных в одну фазу, при U_л=380В(U_ф=220В)

С_ф = Q_к10⁶/942 U =23,32·10⁶/942·220²=511 мкФ

7. Реальная активная мощность двух АД

P = =(18,5/0,9)0,6+(30/0,91)0,8=12,33+26,37=38,71 кВт

8.Потери мощности питающей линии пропорциональны току нагрузки в квадрате

Таким образом, при компенсации реактивной мощности потери в линии снижаются на 26,5 %