Вопрос№6

Основное уравнение гидростатики геометрический смысл

Так как: p + g × z = const, то p/g + z = const [м] - основное уравнение гидростатики.

Вопрос№7

При движении сосуда на частицы жидкости, кроме сил тяжести действуют еще силы инерции, под действием этих сил жидкость принимает новое положение равновесия. Такое равновесие жидкости называется относительным покоем.

Относительным покоем называется равновесие жидкости в движущемся сосуде, находящейся под действием сил тяжести и инерции.

При относительном покое положение свободной поверхности и поверхностей уровня, отличается от их положения для жидкости в неподвижном сосуде.

Для определения формы и положения этих поверхности учитывается основное свойство поверхности уровня. Поверхности уровня – это поверхности равного давления.

Так как dР=0. И из этого выражения следует, что работа массовых сил вдоль поверхности равного давления равна нулю. Это значит, что в состоянии относительного покоя результирующее ускорение перпендикулярно к соответсвующему элементу поверхности равного давления

Ox: X = j - gSinα,Oz : Z = -gCosα,Оx: Y = 0.

Т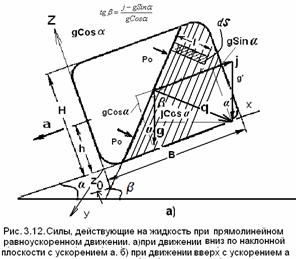

Условие равновесия указанного объема жидкости в направлении нормали к свободной поверхности будет иметь вид

РdS = P0dS + q(ρldS),

коэффициент в линейном уравнении равен тангенсу угла β

где последний член представляет собой полную массовую силу q – суммарная единичная массовая сила, действующая на выделенный объем жидкости массой М= ρldS– масса, а l — расстояние от точки М до свободной поверхности.После сокращения на dS получимР = P0 + qρl.

Вопрос№8

Покой при равномерном вращении сосуда с жидкостью

Рассмотрим сосуд с жидкостью, вращающийся вокруг вертикальной оси с постоянной скоростью Й. На жидкость действуют внешнее давление, силы тяжести и инерционные силы. В результате их действия жидкость принимает новое равновесное положение. Свободная поверхность принимает форму параболоида. Рассмотрим на этой поверхности произвольную точку N. Равнодействующая сила F, действующая в т. N, перпендикулярна к свободной поверхности. Величина этой силы увеличивается с увеличением радиуса, а угол её наклона к горизонту уменьшается. Из этого следует, что наклон этой поверхности к горизонту увеличивается с ростом радиуса. Таким образом, сила R определяет форму свободной поверхности. Найдём математическую формулу этой кривой.

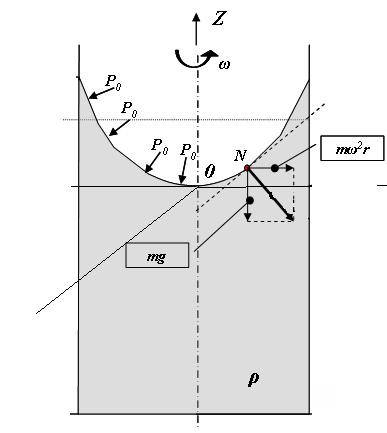
Для данного случая относительного покоя силу F можно разложить на две силы, сила тяжести G и инерции Fин.

Силу инерции можно разложить на две составляющие Fин х и Fин y.

Определим давление в жидкости, используя полный дифференциал давления

С учётом этого полный дифференциал давления примет вид

Проинтегрируем эту функцию

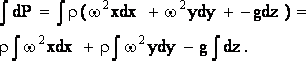
Результатом интегрирования будет являться выражение

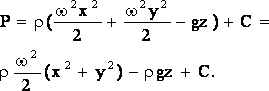
Учитывая, что , где r – радиус вращения, получим

Постоянную интегрирования C определим из условия, что при , тогда . Постоянная интегрирования с учётом принятых условий будет

Тогда формула, выражающая давление в жидкости, вращающейся с постоянной угловой скоростью, примет вид

Заметим, что в итоговом выражении первое слагаемое, характеризует давление внешней среды. Второе слагаемое описывает давление, созданное столбом жидкости, находящейся ниже точки 0, т.е. глубиной под уровнем нулевой точки. Третье слагаемое характеризуется высотой над точкой 0, и, следовательно, описывает давление, создаваемое жидкостью, поднимающейся по краям сосуда, причём эта величина зависит от расстояния точки от оси вращения. Таким образом, оказывается, что давление в каждой точке жидкости, вращающейся с постоянной скоростью относительно вертикальной оси, складывается из внешнего давления и давления столба жидкости над этой точкой.

Найдем поверхности равного давления. dр=0 то уравнение примет вид