
- •2. Удельный вес
- •3. Относительный удельный вес
- •5. Относительный удельный вес
- •6. Температурное расширение жидкости
- •8. Кипение
- •9. Сопротивление растяжению жидкостей
- •10. Вязкость
- •Вопрос№3
- •Вопрос№4
- •Вопрос№5
- •Вопрос№6
- •Вопрос№7
- •Вопрос№8
- •Вопрос№9
- •Вопрос№10
- •Вопрос№11
- •Вопрос№12
- •Вопрос№13
- •Вопрос№14 Вопрос№15
- •Вопрос№16
- •Вопрос№17
- •Вопрос№18
- •Вопрос№19
- •Вопрос№20
- •Вопрос№21
- •Вопрос№22
- •Вопрос№23
- •Вопрос№24
- •Вопрос№25
- •Вопрос№26
- •Вопрос№27
- •Вопрос№28 Вопрос№29
- •Вопрос№30
- •Вопрос№31
- •Вопрос№32
- •Вопрос№33
- •Вопрос№34
- •Вопрос№35
- •Вопрос№36
- •Вопрос№37
- •Вопрос№38 динамические нагнетатели
- •Вопрос 39
- •40_41__ Рабочий процесс лопастного насоса
- •42___ Основное уравнение лопастных насосов.
- •43____ Гидравлические характеристики центробежного насоса.
- •45____ Классификация насосов по коэффициенту быстроходности Быстроходность и тип насоса
- •46___Работа насоса на сеть. Работа насоса на сеть
- •47___ Параллельная работа насосов на сеть
- •48____ Последовательная работа насосов на сеть
- •49___Основы сельскохозяйственного водоснабжения
- •50___ Системы водоснабжения. Источники водоснабжения Источники водоснабжения
- •[Править]Система водоснабжения
- •[Править]Основные элементы системы водоснабжения
- •[Править]Классификация систем водоснабжения
- •51____ Категори надежности подачи воды систем водоснабжения
- •52____ Групповые водопроводы. Преимущества недостатки групповых водопроводов.
- •55___ Осушительно-увлажнительная система. Преимущества недостатки.
- •56____ Г идравлический и пневматический транспорт. Назначение и общее устройство гидротранспортных установок. Трубопроводный транспорт
- •Вопрос57
- •Вопрос58
- •Вопрос 59-60 Расчет гидро-пневмотранспортных установок
Вопрос№4
Основное уравнение гидростатики
Определим теперь величину давления внутри покоящейся жидкости. С этой целью рассмотрим произвольную точку А, находящуюся на глубине ha. Вблизи этой точки выделим элементарную площадку dS. Если жидкость покоится, то и т. А находится в равновесии, что означает уравновешенность сил, действующих на площадку.
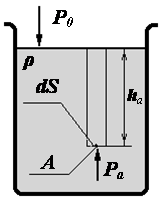
A – произвольная точка в жидкости, ha – глубина т. А, P0 - давление внешней среды,
r - плотность жидкости, Pa – давление в т. А, dS – элементарная площадка.
Сверху
на площадку действует внешнее давление
P0 (в случае, если свободная поверхность
граничит с атмосферой, то![]() ) и вес столба жидкости. Снизу – давление
в т. А. Уравнение сил, действующих на
площадку, в этих условиях примет вид:
) и вес столба жидкости. Снизу – давление
в т. А. Уравнение сил, действующих на
площадку, в этих условиях примет вид:
![]()
Разделив это выражение на dS и учтя, что т. А выбрана произвольно, получим выражение для P в любой точке покоящейся жидкости:
![]()
где h – глубина жидкости, на которой определяется давление P.
Полученное выражение носит название основного уравнения гидростатики.
Вопрос№5
Сначала рассмотрим простейший случай покоя. Жидкость находится под действием силы тяжести. Это означает, что проекции ускорений на оси X и Y отсутствуют. Единственным ускорением является ускорение свободного падения g, т. е.:
![]() ,
,![]() ,
,
![]()
Тогда полный дифференциал давления после подстановки в него ускорений примет вид:
![]()
После интегрирования этого выражения получим:
![]()
Постоянную интегрирования, равную
![]()
найдём,
подставив параметры свободной поверхности
![]() и
и
![]()
После подстановки этих значений в интеграл P будем иметь равенство:
![]()
Переписав это выражение в другом виде, получим
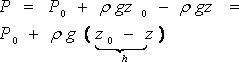
Если обозначить (Z0 - Z) через h, то приведённое равенство примет уже знакомый вид основного уравнения гидростатики
![]()
Из этого же равенства можно получить следующий вид
![]()
или
![]() Последнее
выражение часто называют
основным законом гидростатики.
Последнее
выражение часто называют
основным законом гидростатики.
2) Физический смысл основного закона гидростатики – закон сохранения энергии для покоящейся жидкости, который говорит о том, что механическая энергия любой частицы жидкости одинакова. В этом выражении:
![]() -
потенциальная энергия единицы веса
жидкости, определяемая положением над
нулевой линией,
-
потенциальная энергия единицы веса
жидкости, определяемая положением над
нулевой линией,
![]() -
потенциальная энергия единицы веса
жидкости, зависящая от степени её сжатия.
-
потенциальная энергия единицы веса
жидкости, зависящая от степени её сжатия.
В геометрической интерпретации константу обозначают буквой H и называют гидростатическим напором, а саму формулу записывают в виде:
![]()
Слагаемые основного закона гидростатики в этом случае называют:
 -
нивелирная высота,
- пьезометрическая высота.
-
нивелирная высота,
- пьезометрическая высота.
Второй случай,когда поверхность равного давления может быть наклонной. Например, свободная поверхность бензина в железнодорожной цистерне, движущейся горизонтально с ускорением а (рис)
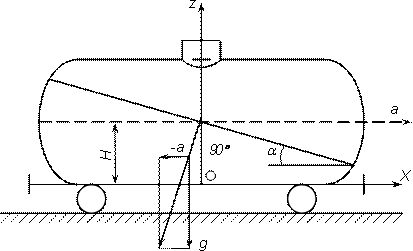
В этом случае единичная масса жидкости находится под действием силы тяжести Z= -1 *g и горизонтального ускорения силы инерции Х= -1*а (к цистерне приложена сила с ускорением а, а к жидкости—такая же по величине сила инерции с ускорением - а).
Составляющие массовых сил в уравнении получают значения:
![]()
Из вышеизложенного следует, что свободная поверхность бензина в цистерне представляет собой плоскость с углом наклона
![]()
Уравнение в этом случае примет вид
![]()
После интегрирования получим зависимость распределения давления в любой точке цистерны с бензином:
![]()
Из этого выражения следует, что наибольшее давление будет в точке z=0 и максимальным отрицательным значением х.
