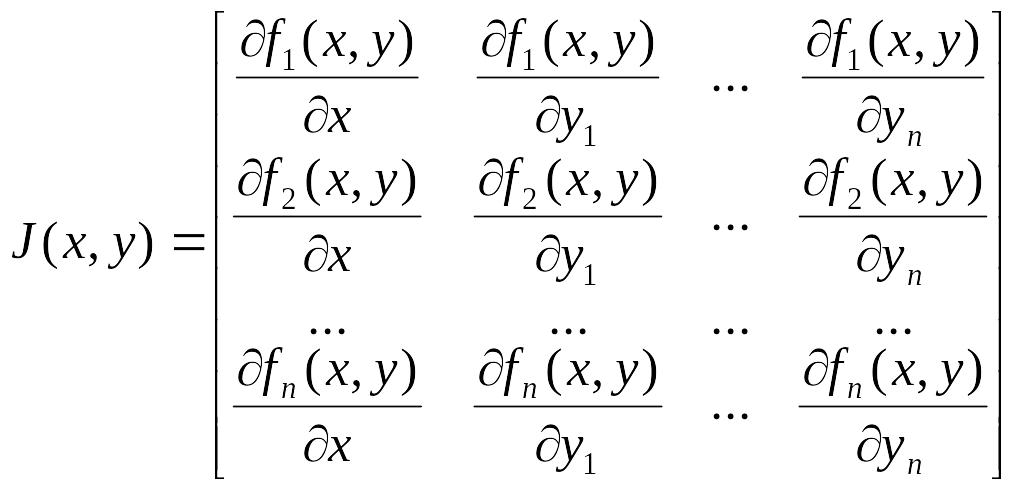Генератор на туннельном диоде.

Генератор на туннельном диоде, имеющем нелинейную N-образную вольт-амперную характеристику (ВАХ). Пусть туннельный диод подключен к источнику постоянного напряжения Е , через последовательно соединенные резистор R и индуктор L. Пусть далее R и E выбраны так, что рабочая точка туннельного диода находится на падающем участке его ВАХ. Это обстоятельство принципиально важно, поскольку дифференциальная проводимость туннельного диода тогда является отрицательной. Физически это означает, что туннельный диод отдает энергию во внешнюю цепь.

Если учесть емкость C туннельного диода (совместно с емкостью монтажа и нагрузочной емкостью), то такая схема будет описываться следующей системой нелинейных дифференциальных уравнений:

, .

Нелинейность этой системы обусловлена тем, что во втором уравнении ток туннельного диода I(u) нелинейно зависит от напряжения на нем и емкости C - u. Зависимость I(u) есть N-образная вольт--амперная характеристика туннельного диода.

Средства среды MathCad

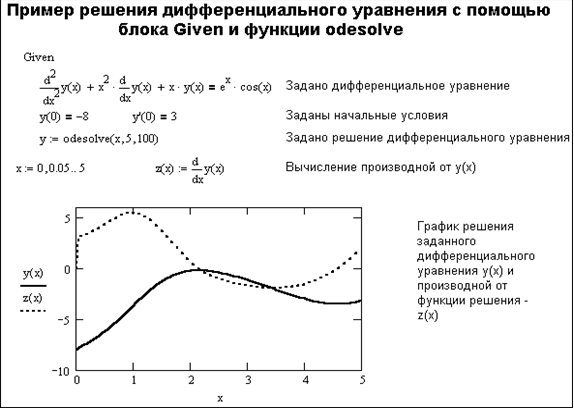
Решение ОДУ с помощью функции odesolve

Начиная с Mathcad 2000, была введена новая функция для решения одиночных дифференциальных уравнений.

Odesolve(x,b,[число шагов]),которая возвращает решение дифференциального уравнения, описанного в блоке Given, при заданных начальных условиях и в конце интервала интегрирования b.

Эта функция имеет ряд особенностей. Если указан параметр число шагов, то решение выполняется с фиксированным шагом, иначе — адаптивным методом. Хотя аналитическое выражение для этой функции не выводится, с ней можно выполнять математические преобразования, например, дифференцировать.

Решение систем оду

Для численного решения систем ДУ в Mathcad введен ряд функций. Вначале остановимся на функциях, дающих решения для систем обыкновенных дифференциальных уравнений, представленных в обычной форме Коши:

rkadapt(y,x1,x2,acc,n,F,k,s) — возвращает матрицу, содержащую таблицу значений решения задачи Коши на интервале от x1 до x2 для системы обыкновенных дифференциальных уравнений, вычисленную методом Рунге-Кутта с переменным шагом и начальными условиями в векторе y (правые части системы записаны в векторе F, n — число шагов, k — максимальное число промежуточных точек решения, и s — минимально допустимый интервал между точками);

Rkadapt(y,x1,x2,n,F) — возвращает матрицу решений методом Рунге-Кутта с переменным шагом для системы обыкновенных дифференциальных уравнений с начальными условиями в векторе y, правые части которых записаны в символьном векторе F на интервале от x1 до x2 при фиксированном числе шагов n;

rkfixed(y,x1,x2,n,F) — возвращает матрицу решений методом Рунге-Кутта системы обыкновенных дифференциальных уравнений с начальными условиями в векторе y, правые части которых записаны в символьном векторе F на интервале от x1 до x2 при фиксированном числе шагов n.

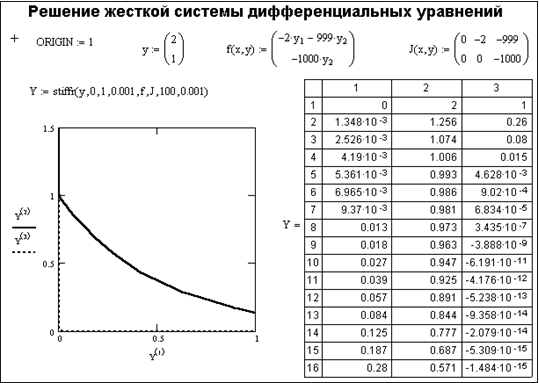
Решение жестких систем ОДУ

Система дифференциальных уравнений, записанная в матричной форме y = A×x, где A — почти вырожденная матрица, называется жесткой. Решение таких систем характерно резко различной скоростью изменения значений переменных и требует очень малого шага, выбираемого исходя из наивысшей скорости изменения значений переменных. Оно подчас невозможно указанными выше методами, дающими недопустимо большую ошибку при решении таких задач. Для решения жестких дифференциальных уравнений в Mathcad введен ряд функций:

bulstoer(y,x1,x2,acc,n,F,k,s) — возвращает матрицу решения системы обыкновенных дифференциальных уравнений на интервале от x1 до x2, правая часть которых записана в символьном векторе F с заданными в векторе y начальными условиями (используется метод решения Булирша-Штера с переменным шагом, параметры k и s задают максимальное число промежуточных точек, на которых ищется решение, и минимально допустимый интервал между ними);

Stiffb(y,x1,x2,n,F,J) — возвращает матрицу решений жесткого дифференциального уравнения, записанного в векторе F и функции Якобиана J, y — вектор начальных значений на интервале [x1,x2] (для решения используется метод Булирша-Штера);

stiffb(y,x1,x2,acc,n,F,J,k,s) — возвращает матрицу решений только в конечной точке жесткого дифференциального уравнения, записанного в векторе F и функции Якобиана J, y — вектор начальных значений на интервале [x1,x2] (для решения используется метод Булирша-Штера с переменным шагом);

stiffr(y,x1,x2,acc,n,F,J,k,s) — матрица решений только в конечной форме жесткого дифференциального уравнения, записанного в векторе F и функции Якобиана J, y — вектор начальных значений на интервале [x1,x2] (для решения используется метод Розенброка с переменным шагом).

В приведенных функциях: acc — погрешность решения (рекомендуется порядка 0.001), k — максимальное число промежуточных точек, и s — минимально допустимый интервал между точками, в которых ищется решение. Обратите внимание, что функции, начинающиеся с малой буквы, дают решения только для конечной точки. Матрица-функция Якоби J, фигурирующая в этих функциях, имеет размер n ´ (n+1) и представляется в виде: