
Комплексные числа. Геометрическое изображение. Равенство комплексных чисел. Комплексно-сопряженные числа.
Ко́мпле́ксные[1] чи́сла (устар. Мнимые
числа[2]),
— расширение множества вещественных
чисел,
обычно обозначается
.
Любое комплексное число может быть
представлено как формальная сумма ![]() ,
где
,
где ![]() и
и ![]() —
вещественные числа,
—
вещественные числа, ![]() — мнимая
единица[3].
— мнимая
единица[3].
Комплексные
числа образуют алгебраически
замкнутое поле —
это означает, что многочлен степени ![]() с
комплексными коэффициентами имеет
ровно
комплексных
корней (основная
теорема алгебры).
Это одна из главных причин широкого
применения комплексных чисел в
математических исследованиях. Кроме
того, применение комплексных чисел
позволяет удобно и компактно сформулировать
многие математические модели, применяемые
в математической физике и в естественных
науках — электротехнике, гидродинамике, картографии, квантовой
механике, теории
колебаний и
многих других.
с
комплексными коэффициентами имеет
ровно
комплексных
корней (основная
теорема алгебры).
Это одна из главных причин широкого
применения комплексных чисел в
математических исследованиях. Кроме
того, применение комплексных чисел
позволяет удобно и компактно сформулировать
многие математические модели, применяемые
в математической физике и в естественных
науках — электротехнике, гидродинамике, картографии, квантовой
механике, теории
колебаний и
многих других.
Определения
Поле
комплексных чисел можно понимать
как расширение
поля вещественных
чисел, в котором многочлен ![]() имеет
корень. Следующие две
элементарные модели показывают,
что непротиворечивое построение такой
системы чисел возможно. Оба приведенных
определения приводят к изоморфным расширениям
поля вещественных чисел
,
как и любые другие конструкции поля
разложения многочлена
.
имеет
корень. Следующие две
элементарные модели показывают,
что непротиворечивое построение такой
системы чисел возможно. Оба приведенных
определения приводят к изоморфным расширениям
поля вещественных чисел
,
как и любые другие конструкции поля
разложения многочлена
.
Стандартная модель
Комплексное
число ![]() можно
определить как упорядоченную
пару вещественных
чисел
можно
определить как упорядоченную
пару вещественных
чисел ![]() .
Введём операции сложения и умножения
таких пар следующим образом:
.
Введём операции сложения и умножения
таких пар следующим образом:
Вещественные
числа являются в этой модели подмножеством
множества комплексных чисел и представлены
парами вида ![]() ,
причём операции с такими парами
согласованы с обычными сложением и
умножением вещественных чисел. Ноль
представляется парой
,
причём операции с такими парами
согласованы с обычными сложением и
умножением вещественных чисел. Ноль
представляется парой ![]() единица
—
единица
— ![]() а мнимая
единица —
а мнимая
единица — ![]() На
множестве комплексных чисел ноль и
единица обладают теми же свойствами,
что и на множестве вещественных, а
квадрат мнимой единицы, как легко
проверить, равен
На
множестве комплексных чисел ноль и
единица обладают теми же свойствами,
что и на множестве вещественных, а
квадрат мнимой единицы, как легко
проверить, равен ![]() ,
то есть
,
то есть ![]()
Несложно показать, что определённые выше операции имеют те же свойства, что и аналогичные операции с вещественными числами. Исключением являются только свойства, связанные с отношением порядка (больше-меньше), потому что расширить порядок вещественных чисел, включив в него все комплексные числа так, чтобы операции по-прежнему были согласованы с порядком, невозможно.
Матричная модель
Комплексные числа можно также определить как семейство вещественных матриц вида
![]()
с обычным матричным сложением и умножением. Действительной единице будет соответствовать
![]()
мнимой единице —
![]()
Замечания
Ошибочно
определение числа
как
единственного числа, удовлетворяющего
уравнению ![]() ,
так как число
,
так как число ![]() также
удовлетворяет этому уравнению.
также
удовлетворяет этому уравнению.
Следует
также заметить, что выражение ![]() ,
ранее часто использовавшееся вместо
,
не вполне корректно, так как алгебраический
корень определяется над множеством
неотрицательных чисел. Вплоть до конца
XIX века запись вроде
,
ранее часто использовавшееся вместо
,
не вполне корректно, так как алгебраический
корень определяется над множеством
неотрицательных чисел. Вплоть до конца
XIX века запись вроде ![]() считалась
допустимой, но в настоящее время, во
избежание ошибок, принято записывать
это выражение как
считалась
допустимой, но в настоящее время, во
избежание ошибок, принято записывать
это выражение как ![]() .
Пример возможной ошибки при неосторожном
использовании устаревшей записи:
.
Пример возможной ошибки при неосторожном
использовании устаревшей записи:
![]()
в то время как правильная запись приводит к иному ответу:
![]()
Действия над комплексными числами
Сравнение
![]() означает,
что
означает,
что ![]() и
и ![]() (два
комплексных числа равны между собой
тогда и только тогда, когда равны их
действительные и мнимые части).
(два
комплексных числа равны между собой
тогда и только тогда, когда равны их
действительные и мнимые части).
Сложение
![]()
Вычитание
![]()
Умножение
![]()
Деление
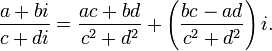
Геометрич. изображение
Действительные числа можно изобразить точками прямой линии, как показано на фиг. 2, где точка А изображает число 4, а точка В – число – 5. Эти же числа можно изображать также отрезками ОА, ОВ, учитывая не только их длину, но и направление.
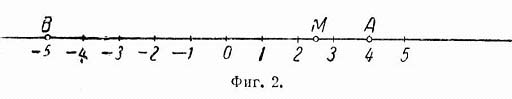
Каждая
точка М «числовой прямой» изображает
некоторое действительное число
(рациональное, если отрезок ОM соизмерим
с единицей длины, и иррациональное, если
несоизмерим). Таким образом, на числовой
прямой не остается места для комплексных
чисел.
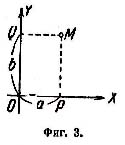
Но комплексные числа можно
изобразить на «числовой плоскости».
Для этого мы выбираем на плоскости
прямоугольную систему координат с одним
и тем же масштабом на обеих осях (фиг.
3). Комплексное число a +bi мы изображаем
точкой М, у которой абсцисса х (на фиг.
3 х = ОР = QM) равна абсциссе а комплексного
числа ордината у (ОQ = РМ) равна ординате
b комплексного числа.
Примеры. На фиг.
4 точка A с абсциссой х = 3 и ординатой у
= 5 изображает комплексное число 3 + 5i .
Точка В изображает комплексное число
– 2 + 6i; точка C комплексное число – 6 –
2i; точка D – комплексное число 2 –
6i.
Д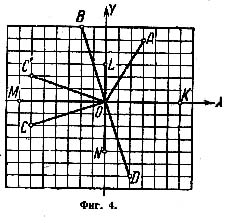 ействительные
числа (в комплексной форме они имеют
вид a + 0i) изображают точками оси X, а чисто
мнимый (вида 0 + bi) – точками оси Y. Примеры.
Точка К на фиг. 4 изображает действительное
число 6 (или, что то же, комплексное число
6 + 0i), точка L — чисто мнимое число 3i (т.
е. 0 + 3i); точка N - чисто мнимое число – 4i
(т. е. 0 – 4i). Начало координат изображает
число 0 (т. е. 0 + 0i ).
Сопряженные
комплексные числа изображаются парой
точек, симметричных относительно оси
абсцисс; так, точки С и С' на фиг. 4
изображают сопряженные числа – 6 – 2i и
– 6 + 2i. Комплексные числа можно изображать
также Отрезками («векторами»), начинающимися
в точке О и оканчивающимися в соответствующей
точке числовой плоскости. Так, комплексное
число – 2 + 6i можно изобразить не только
точкой В (фиг. 4), но также вектором ОB;
комплексное число - 6 – 2i изображается
вектором ОС и т. д.
Замечание. Давая
какому-либо отрезку наименование
«вектор», мы подчеркиваем, что существенное
значение имеет не только длина, но и
направление отрезка. Два вектора
считаются одинаковыми (равными) только
в том случае, когда они имеют одинаковую
длину и одно и то же направление.
ействительные
числа (в комплексной форме они имеют
вид a + 0i) изображают точками оси X, а чисто
мнимый (вида 0 + bi) – точками оси Y. Примеры.
Точка К на фиг. 4 изображает действительное
число 6 (или, что то же, комплексное число
6 + 0i), точка L — чисто мнимое число 3i (т.
е. 0 + 3i); точка N - чисто мнимое число – 4i
(т. е. 0 – 4i). Начало координат изображает
число 0 (т. е. 0 + 0i ).
Сопряженные
комплексные числа изображаются парой
точек, симметричных относительно оси
абсцисс; так, точки С и С' на фиг. 4
изображают сопряженные числа – 6 – 2i и
– 6 + 2i. Комплексные числа можно изображать
также Отрезками («векторами»), начинающимися
в точке О и оканчивающимися в соответствующей
точке числовой плоскости. Так, комплексное
число – 2 + 6i можно изобразить не только
точкой В (фиг. 4), но также вектором ОB;
комплексное число - 6 – 2i изображается
вектором ОС и т. д.
Замечание. Давая
какому-либо отрезку наименование
«вектор», мы подчеркиваем, что существенное
значение имеет не только длина, но и
направление отрезка. Два вектора
считаются одинаковыми (равными) только
в том случае, когда они имеют одинаковую
длину и одно и то же направление.
Сопряжённые числа

![]()
Геометрическое представление сопряжённых чисел
Если
комплексное число ![]() ,
то число
,
то число ![]() называется сопряжённым (или
комплексно сопряжённым) к
(обозначается
также
называется сопряжённым (или
комплексно сопряжённым) к
(обозначается
также ![]() ).
На комплексной плоскости сопряжённые
числа получаются зеркальным отражением
друг друга относительно вещественной
оси. Модуль сопряжённого числа такой
же, как у исходного, а их аргументы
отличаются знаком.
).
На комплексной плоскости сопряжённые
числа получаются зеркальным отражением
друг друга относительно вещественной
оси. Модуль сопряжённого числа такой
же, как у исходного, а их аргументы
отличаются знаком.
Переход к сопряжённому числу можно рассматривать как одноместную операцию; перечислим её свойства.
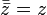 (сопряжённое
к сопряжённому есть исходное).
(сопряжённое
к сопряжённому есть исходное).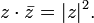
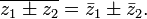
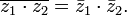
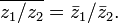
Обобщение: ![]() ,
где
,
где ![]() —
произвольный многочлен с вещественными
коэффициентами.
—
произвольный многочлен с вещественными
коэффициентами.
Значимость
сопряжения объясняется тем, что оно
является образующей группы
Галуа ![]() .
.
