
Квадратичные формы и их применение
Определение. Квадратичной
формой ![]() переменных
переменных ![]() ,принимающих
числовые значения , называется числовая
функция вида
,принимающих
числовые значения , называется числовая
функция вида
![]()
![]()
![]() ,
,
где ![]() -
числа, называемые коэффициентами
квадратичной формы.
-
числа, называемые коэффициентами
квадратичной формы.
Определение. Матрицей
квадратичной формы
переменных
,
называется симметрическая матрица
порядка
,
элементы главной диагонали которой
совпадают с коэффициентами при квадратах
переменных, а каждый недиагональный
элемент, расположенный в ![]() ой
строке
ой
строке ![]() ом
столбце, равен половине коэфициента
при
ом
столбце, равен половине коэфициента
при ![]() в
квадратичной форме.
в
квадратичной форме.
Определение. Рангом
квадратичной формы называется ранг её
матри-цы. Квадратичная форма может
быть записана в матричном виде ![]() где
где ![]() матрица
квадратичной формы и
матрица
квадратичной формы и ![]() .
.
Определение.
Квадратичная форма называется канонической
(имеет канонический вид), если
коэфициенты ![]() при
при ![]() ,
то есть, если матрица квадратичной формы
диагональная и следовательно
,
то есть, если матрица квадратичной формы
диагональная и следовательно
![]()
![]() .,
.,
где
не все коэффициенты ![]() равны
нулю.
равны
нулю.
Теорема (Лагранжа). Для всякой квадратичной формы существует такой базис, в котором квадратичная форма имеет канонический вид.
Определение.
Нормальным видом квадратичной формы
называется такой канонический вид, в
котором коэффициенты при квадратах
неизвестных (не считая нулевых) равны ![]() .
.
Определение.
Квадратичная форма ![]() называется
положительно
называется
положительно
(отрицательно)
определённой, если ![]() при
всех
при
всех
![]() и
положительно (отрицательно)
полуопределённой,если
и
положительно (отрицательно)
полуопределённой,если ![]() при
всех
при
всех ![]() .
.
Теорема (критерий Сильвестра). Для того чтобы квадратичная форма была положительно определённой, необходимо и достаточно чтобы все угловые миноры матрицы квадратичной формы были положительны,то есть, чтобы
![]()
Здесь ![]() -угловые
миноры матрицы квадратичной формы.
-угловые
миноры матрицы квадратичной формы.
Следствие.
Для того чтобы квадратичная форма
была
отрицательно определённой, необходимо
и достаточно, чтобы знаки угловых миноров
матрицы квадратичной формы чередовались
следующим образом: ![]()
Примеры
1. Привести квадратичную форму к каноническому виду методом Лагранжа и записать соответствующее преобразование
![]() .
.
Решение. Следуя
алгоритму метода Лагранжа, выделим
вначале в квад-ратичной форме все члены,
содержащие ![]() ,
и дополним их до полного квадрата:
,
и дополним их до полного квадрата:
![]() .
.
Сделаем
в этом выражении замену ![]() и
подставим его в квадратичную форму.
Получим:
и
подставим его в квадратичную форму.
Получим:
![]() .
.
Далее
выделим в ![]() члены,
содержащие
члены,
содержащие ![]() и
проделаем с ними анало-гичную процедуру:
и
проделаем с ними анало-гичную процедуру:
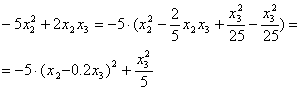
Если
положить ![]() ,
то квадратичная форма уже не будет
содержать смешанных произведений. Примем
также
,
то квадратичная форма уже не будет
содержать смешанных произведений. Примем
также ![]() ,
тогда
,
тогда
канонический вид квадратичной формы есть
![]() .
.
Соответствующее
преобразование от переменных ![]() к
переменным
к
переменным ![]() имеет
вид:
имеет
вид:
![]() .
.
2. Найти ортогональное преобразование, приводящее квадратичную форму к каноническому виду, и записать соответствующий канонический вид этой формы:
![]() .
.
Решение. В
исходном базисе ![]() матрица
оператора, соответствующая данной
квадратичной форме, есть
матрица
оператора, соответствующая данной
квадратичной форме, есть
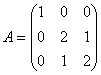 .
.
Эта
матрица будет определять квадратичную
форму канонического вида в
ортонормированном базисе ![]() ,
составленном из собственных векторов
матрицы
,
составленном из собственных векторов
матрицы ![]() . Найдем
их.
. Найдем
их.
Характеристическое уравнение для матрицы имеет вид
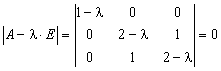 .
.
Откуда следует
![]() и
и ![]() .
.
Как известно собственные векторы матрицы находятся из уравнений
![]() .
.
Для
случая ![]() имеем:
имеем:
![]()
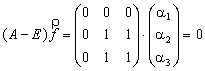 .
.
Ранг
матрицы этой системы уравнений
(относительно ![]() )
равен 1. Следовательно, ФСР системы
состоит из двух линейно независимых
решений.
)
равен 1. Следовательно, ФСР системы
состоит из двух линейно независимых
решений.
Как
видно из данной системы, величина ![]() принимает
произвольные значения, а величины
принимает
произвольные значения, а величины ![]() связаны
соотношением
связаны
соотношением ![]() . В
качестве собственных можно выбрать,
например, векторы
. В
качестве собственных можно выбрать,
например, векторы
![]()
Эти
векторы ортогональны: ![]() (если
бы они оказались не ортогональными, то
их нужно было бы ортогонализировать с
помощью стандартной процедуры). Вектор
(если
бы они оказались не ортогональными, то
их нужно было бы ортогонализировать с
помощью стандартной процедуры). Вектор ![]() к
тому же и нормирован. Откуда следует
-
к
тому же и нормирован. Откуда следует
- ![]() . Нормируем
теперь вектор
. Нормируем
теперь вектор![]() :
:
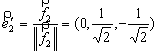 .
.
Для
случая ![]() уравнение,
определяющее собственный вектор есть
уравнение,
определяющее собственный вектор есть
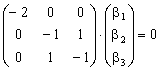 .
.
Ранг
матрицы этой системы уравнений равен
2. Следовательно она имеет одно линейно
независимое решение, например, ![]() Отнормируем
этот вектор:
Отнормируем
этот вектор: 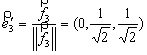 .
.
Теперь можно составить искомую матрицу ортогонального преобразования:
 .
.
Исходная квадратичная форма будет иметь следующий канонический вид
![]() .
.
При
этом переменные ![]() связаны
с переменными
соотношением
связаны
с переменными
соотношением
 или
или
![]()
3. Построить в прямоугольной системе координат фигуру, определяемую следующим уравнением, предварительно приведя его к каноническому виду
![]() .
.
Решение. Выделим
в этом выражении квадратичную форму ![]() .
Это три первых слагаемых уравнения
.
Это три первых слагаемых уравнения ![]() .
.
Матрица
квадратичной формы равна ![]() .
Проведём процедуру приведения квадратичной
формы к каноническому виду с помощью
ортогонального преобразования.
Характеристическое уравнение матрицы
имеет вид
.
Проведём процедуру приведения квадратичной
формы к каноническому виду с помощью
ортогонального преобразования.
Характеристическое уравнение матрицы
имеет вид
![]() .
.
Его
корни таковы: ![]() .
.
Найдём
теперь собственные векторы, соответствующие
этим корням и отнормрируем их. Для
вектора ![]() ,
соответствующего
,
соответствующего
![]() ,
имеем
,
имеем
![]()
В итоге собственный вектор, соответствующий , можно выбрать в виде
![]() .
.
Анологичная
процедура для собственного вектора ![]() даёт:
даёт: ![]()
Откуда:
![]() .
.
После нормировки полученных векторов имеем:
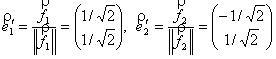 .
.
Эти
векторы представляют собой ортонормированный
базис новой системы координат. Матрица
ортогонального оператора, приводящего
квадратичную форму ![]() к
каноническому виду
к
каноническому виду ![]() ,
есть
,
есть
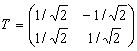
Связь
старых ![]() и
новых
и
новых ![]() координат
определяется соотношением
координат
определяется соотношением 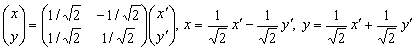 .
.
Учитывая приведенные выражения, приведём заданную квадратичную форму к каноническому виду
 Это
есть каноническое уравнение эллипса в
системе координат
Это
есть каноническое уравнение эллипса в
системе координат ![]() ,которая
получается из исходной её поворотом на
угол
,которая
получается из исходной её поворотом на
угол ![]() и
переносом начала координат в точку
и
переносом начала координат в точку ![]() .
.
