- •19. Магнитное поле и его характеристики
- •20.Закон Ампера
- •22.Действие магнитного поля на движущийся заряд
- •23.Контур с током в однородном и неоднородном магнитном поле.
- •24.Работа по перемещению проводника и контура с током в магнитном поле
- •25. Явление электромагнитной индукции (опыты Фарадея)
- •26. Индуктивность в контуре. Самоиндукция
Вопрос №1 Электрический заряд. Дискретность электрического заряда. Элементарный заряд. Закон сохранения электрического заряда. Опыт Милликэна. Закон Кулона. Система единиц. Диэлектрическая постоянная. Линейная, поверхностная и объемная плотность зарядов.
Электрический заряд – количественная мера действия степени электризации тел.
Элементарный заряд - минимальная порция электрического заряда (e=1.6-19), заряд элементарной частицы (электрон, протон, нейтрон)
Электрический заряд дискретен, т.е. заряд любого тела составляет целое кратное от элементарного электрического заряда е.
ЗСЭЗ: алгебраическая сумма эл. зарядов любой замкнутой системы не изменяется.
Опыт Милликена: (1909) Между пластинами подавалось напряжение и, с помощью пульверизатора, капельки масла, в микроскоп велось наблюдение за установлением равновесия. Нашёл элементарный заряд.
Закон Кулона: (1785) Сила взаимодействия двух неподвижных точечных зарядов пропорциональна величине каждого из зарядов и обратно пропорциональна квадрату расстояния между ними.
Точечный заряд - Заряженное тело, размерами которого можно пренебречь по сравнению с расстоянием до других тел.
![]()
Также
для з.Кулона справедлив принцип
суперпозиции:
![]() , Fai
– сила, с которой действует qa
на заряд qi
.
, Fai
– сила, с которой действует qa
на заряд qi
.
Опытным путём установлено, что взаимодействие двух электрических зарядов не зависит от наличия других зарядов.
Диэлектрическая
постоянная:
![]() [ф/м]
[ф/м]
Линейная
плотность заряда:
![]() [Кл/м]
[Кл/м]
Поверхностная
плотность заряда:
![]() [кл/м^2]
[кл/м^2]
Объёмная
плотность заряда:
![]() [кл/м^3]
[кл/м^3]
Вопрос №2 Электрическое поле, его характеристики. Напряженность поля (точечного заряда и системы зарядов). Вектор электрического смещения. Графическое изображение электрических полей
Эл. поле – это пространство, окруж-щее заряж. тела, в кажд. точке этого пространства сопоставлено какое-то значение физ. величины.
Характеристики поля: напряжённость электрического поля Е, потенциал Ф, вектор смещения электрического поля D.
Напряжённость поля: векторная физическая величина, равная отношению силы, действующей на заряд, к величине этого заряда. E=F/q.
![]()
Напряжённость поля точечного электрического заряда:
![]()
![]()
Напряжённость поля системы зарядов:
![]()
![]()
Вектор электрического смещения: D=Eεε
![]()
Графическое изображение электрических полей: Линии напряжённости проводят так, что касательная к ним в каждой точке совпадает с направлением вектора Е. Густота линий выбирается так, что кол-во линий, пронизывающих единицу пов-ти, перпендикулярной к линиям площадки, было равно числовому значению Е.
Вопрос №3 Работа перемещения электрического заряда в электрическом поле. Теорема о циркуляции вектора напряженности электрического поля. Потенциал электрического поля. Разность потенциалов. Эквипотенциальные поверхности. Потенциал поля точечного заряда и системы зарядов.

![]()


Кулоновская сила консервативна, а электростатическое поле - потенциально.
Работа
сил консервативного поля – убыль
потенциальной энергии.
![]()
![]()
![]()
Потенциал: скал. физ. велич., равная потенц. эн., которой обладает ед. пол. заряд, помещ. в данную точку. (Wп/qпр)
Потенциал
поля точечного заряда:
![]()
Потенциал
поля системы зарядов:
![]() (алгебраическая
сумма потенциалов, создаваемых каждым
из зарядов в отдельности)
(алгебраическая
сумма потенциалов, создаваемых каждым
из зарядов в отдельности)
Wn=φq A=W1-W2 =q(φ1 – φ2)
A=qφ (если заряд из точки с потенциалом φ удаляется на бесконечность)=>Потенциал: численно равен работе, которую совершают силы поля над единичным полож. зарядом при удалении его из данной точки на бесконечность.
![]()
![]()
Теорема о циркуляции вектора напряжённости(признак потенциальности поля): циркуляция вектора Е равна нулю.
Эквипотенциальные поверхности: воображаемые пов-ти, все точки которых имеют одинаковый потенциал. Уравнение такой пл-ти: φ(x,y,z)=Const
Вектор Е в каждой точке направлен по нормали к эквипот. пов-ти.
Линии напряжённости в каждой точке ортогональны к эквипот. пов-тям.
Эквипот. пов-ть можно провести через любую точку поля => по густоте эквипот. пов-тей можно судить о величине напряжённости поля.
Билет №4
Связь напряженности электрического поля с потенциалом. Применение этой связи для расчета эл. полей.
dA
= qEdl = qEdlCos@ = qEldl; dA = -dWn = -qdφ
=>
![]()
![]()
![]()
Зная Е можно найти разность потенциалов между двумя произвольными точками поля:
и
![]() =>
=>
![]()
Билет №5
Принцип суперпозиции Эл. Полей. Расчет поля (напряженности и потенциала) заряженной нити, кольца
Принцип суперпозиции эл. полей: Напряжённость поля системы зарядов равна векторной сумме напряжённостей полей, которые создавал бы каждый из зарядов в отдельности.
![]()
Напряжённость заряженной нити:
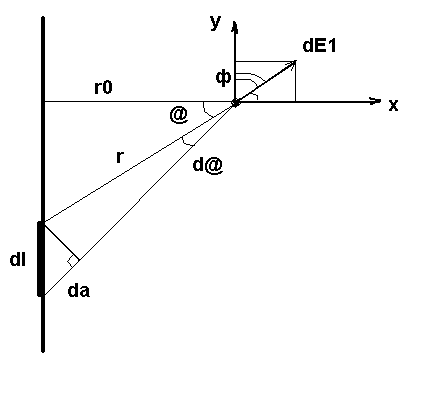
Выберем беск. малый эл-нт dl
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() |
=>
|
=>
![]()
![]() |
|
![]()
![]()
![]()
Частные
случаи: 1) r0
-> ∞ @1 = π/2
@2 = π/2
![]()
![]()
2)Против среза нити @1 = π/2
@2 = 0
![]()
3)Против
середины нити @1 = -@2
![]()
![]() =>
=>
![]()
Билет №6Электрический диполь. Расчет поля диполя
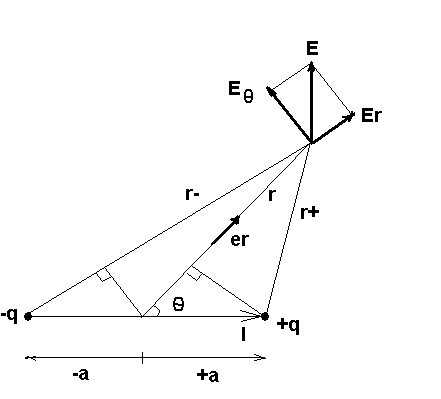
l
= 2a,
a
<< r
=>
![]()
![]()
![]()
![]()
![]()
![]() где
p
= ql
–хар-ка диполя, называемая электрическим
моментом(вектор
р
направлен по оси диполя от – к +)
где
p
= ql
–хар-ка диполя, называемая электрическим
моментом(вектор
р
направлен по оси диполя от – к +)
![]()
тогда
![]()
![]()
![]()
![]()
Если
θ = 0, то напряжённость на оси диполя![]() , этот вектор направлен по оси диполя
от – к + .
, этот вектор направлен по оси диполя
от – к + .
Если
θ = π/2, то напряжённость на прямой,
проходящей через центр диполя и
перпендикулярной к его оси
![]()
Напряжённость диполя убывает с расстоянием от диполя как 1/r^3, т е быстрее, чем напряжённость поля точечного заряда.
Билет №7
Поток вектора. Поток вектора напряженности и Эл. Смещения. Расчет потока вектора E и D поля точечного заряда. Теорема Остроградского-Гаусса

dФА = АdSCos@
@ > 90 => со знаком –
@ < 90 => со знаком +
dФА = A n dS = AndS = AdS0
Условимся, что dS – вектор (направление совпадает с нормалью n)
dФA=AdS
Поток
вектора смещения:
![]()
dФD=DdSCos@
dSCos@=dS0
![]() ,
dS0/r^2
– угол, под которым видна площадка S0
= dΩ
,
dS0/r^2
– угол, под которым видна площадка S0
= dΩ
![]() =>
=>
![]()
![]()
Теорема Остроградского-Гаусса:
1)Условимся, что площадку видно изнутри – телесный угол >0; а если снаружи – то <0. 2)Любая замкнутая пов-ть из точки, где расположен заряд, опирается на телесный угол либо 4π стерад, либо 0 стерад (когда смотрим снаружи)
Теорема: Если поверхность замкнута, то поток вектора смещения либо q, либо 0.
Если поле создаётся системой эл. зарядов (либо зарядом произвольной формы), то поток вектора D равен алгебраической сумме зарядов, охватываемых данной пов-тью.
![]() |
|
![]() |
=>
|
=>
![]()
Билет №8
Применение теоремы Остроградского-Гаусса для расчета Эл. Полей (напряженности и потенциала) бесконечной заряженной плоскости, нескольких бесконечных заряженных плоскостей, бесконечной нити, бесконечного заряженного шара и сферы, цилиндра.
Поле беск. заряж. плоскости
![]()
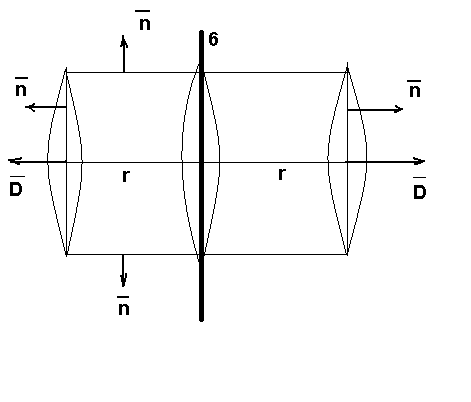
q=σS
2DS=σS
D=σ/2 => поле однородное
![]()
![]()
![]()
![]()
Напряжённость
поля бесконечного цилиндра:![]() λ-
линейная плотность заряда.
λ-
линейная плотность заряда.
![]()
Напряжённость поля заряженной сферической поверхности:
![]() =>
=>
![]() (r
>= R)
Внутри сферы поля нет!
(r
>= R)
Внутри сферы поля нет!
Напряжённость поля объёмно-заряженного шара:
![]() =>
=>
![]() (r
<= R)
(r
<= R)
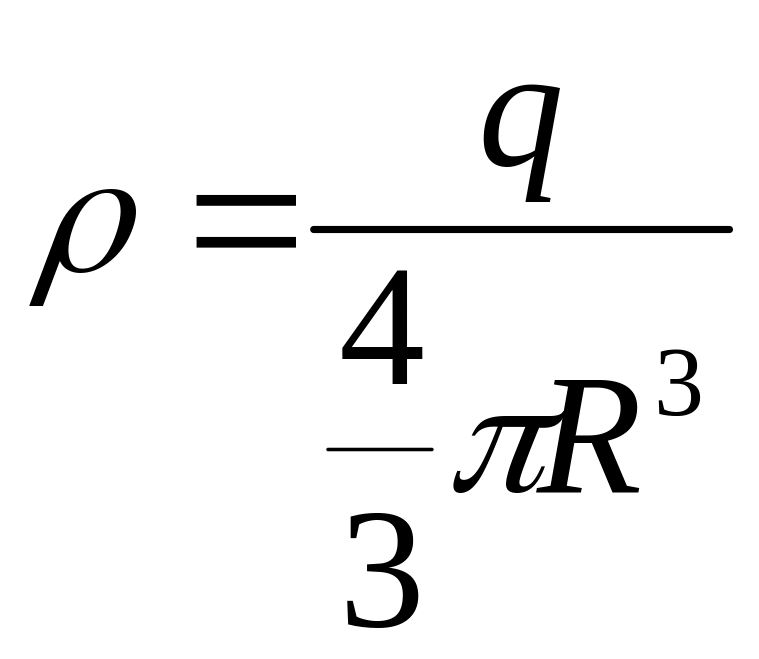
Билет №9
Диэлектрики. Типы диэлектриков. Полярные и неполярные молекулы в Эл. Поле (однородном и неоднородном). Электронная и ориентационная поляризация диэлектриков. Вектор поляризации. Диэлектрическая восприимчивость вещества и ее зависимость от температуры.
Молекулы диэлектриков – диполи. Молекулы: 1)Неполярные (в отсутствии эл. поля Pe=0)
2)Полярные (в отсутсвии эл. поля Pe!=0)
Полярные молекулы в электрическом поле: диполи в Эл. поле стремятся сориентироваться так, что Pe||E. Но есть хаотическое тепловое движение => диполи только стремятся, ориентация преимущественная.(ориентационная поляриз.)
Неполярные
молекулы в электрическом поле:
В поле деформируются
![]() α - поляризуемость молекул (электронная
поляризуемость)
α - поляризуемость молекул (электронная
поляризуемость)
Вектор
поляризации:
Количественная характеристика поляризации
диэлектриков – вектор поляризации –
физическая вел-на, численно равная
суммарному Эл моменту молекул в единице
объёма диэлектрика.
 [Кл/м^2]
[Кл/м^2]
Вектор
поляризации у неполярных диэлектриков:
![]()
αn = 96 – диэлетрическая восприимчивость вещества(«капа»)
P=96ε0E
Вектор поляризации у полярных диэлектриков:
![]() ф-ла
Ланжевена
ф-ла
Ланжевена
![]()
![]()
![]() -
диэлектрическая
восприимчивость
-
диэлектрическая
восприимчивость
![]() -
справедлива
для
всех
диэлектриков(только
96 разные
)
-
справедлива
для
всех
диэлектриков(только
96 разные
)
Билет №10
Электрическое поле в диэлектриках. Свободные и связанные заряды. Поверхностная плотность связанных зарядов. Связь диэлектрической восприимчивости с диэлектрической проницаемостью
При
помещении
диэлектрика
во
внешнее
электрическое
поле
он
поляризуется,
т.
е.
приобретает
отличный
от
нуля
дипольный
момент,
![]() где
где
![]() дипольный момент одной молекулы. Для
количественного описания поляризации
диэлектрика пользуются векторной
величиной — поляризованностью,
определяемой как дипольный момент
единицы объема диэлектрика:
дипольный момент одной молекулы. Для
количественного описания поляризации
диэлектрика пользуются векторной
величиной — поляризованностью,
определяемой как дипольный момент
единицы объема диэлектрика:
![]()
Из
опыта следует, что для большого класса
диэлектриков поляризованность Р линейно
зависит от напряженности поля Е. Если
диэлектрик изотропный и Е не слишком
велико, то
P=![]()
где
![]() — диэлектрическая
восприимчивость вещества,
характеризующая свойства диэлектрика;
- величина безразмерная;
— диэлектрическая
восприимчивость вещества,
характеризующая свойства диэлектрика;
- величина безразмерная;
Для
установления количественных закономерностей
поля в диэлектрике внесем однородное
внешнее электрическое поле
![]() (создается двумя бесконечными параллельными
разноименно заряженными плоскостями)
пластинку из однородного диэлектрика.
Под действием поля диэлектрик поляризуется,
т. е. происходит смешение зарядов:
положительные смещаются по полю,
отрицательные — против поля. В результате
этого на правой грани диэлектрика,
обращенного к отрицательной плоскости,
будет избыток положительного заряда с
поверхностной плотностью +
(создается двумя бесконечными параллельными
разноименно заряженными плоскостями)
пластинку из однородного диэлектрика.
Под действием поля диэлектрик поляризуется,
т. е. происходит смешение зарядов:
положительные смещаются по полю,
отрицательные — против поля. В результате
этого на правой грани диэлектрика,
обращенного к отрицательной плоскости,
будет избыток положительного заряда с
поверхностной плотностью +![]() ',
на левой — отрицательного заряда с
поверхностной плотностью —
'.
Эти заряды, появляющиеся в результате
ионизации диэлектрика, называются
связанными.
Так как их поверхностная плотность
`
меньше плотности
свободных зарядов плоскостей, то не все
поле Е компенсирует полем зарядов
диэлектрика: часть линии напряженности
пройдет сквозь диэлектрик, другая же
часть — обрывается на связанных зарядах.
значит, поляризация диэлектрика вызывает
уменьшение в нем поля по сравнению с
первоначальным внешним полем. Вне
диэлектрика Е=Ео.
',
на левой — отрицательного заряда с
поверхностной плотностью —
'.
Эти заряды, появляющиеся в результате
ионизации диэлектрика, называются
связанными.
Так как их поверхностная плотность
`
меньше плотности
свободных зарядов плоскостей, то не все
поле Е компенсирует полем зарядов
диэлектрика: часть линии напряженности
пройдет сквозь диэлектрик, другая же
часть — обрывается на связанных зарядах.
значит, поляризация диэлектрика вызывает
уменьшение в нем поля по сравнению с
первоначальным внешним полем. Вне
диэлектрика Е=Ео.
Таким
образом, появление связанных зарядов
приводит к возникновению дополнительного
электрического поля Е' (поля, создаваемого
связанными
зарядами), которое направлено против
внешнего поля
(поля, создаваемого свободными
зарядами) и ослабляет его. Результирующее
поле внутри диэлектрика
![]()
Поле
![]() (поле, созданное двумя бесконечными
заряженными плоскостями; см. формулу),
поэтому
(поле, созданное двумя бесконечными
заряженными плоскостями; см. формулу),
поэтому
![]()
Определим
поверхностную
плотность связанных зарядов
![]() '.
Полный
дипольный момент пластинки диэлектрика
'.
Полный
дипольный момент пластинки диэлектрика
![]() где
S
— площадь
грани пластинки,
d
—
ее толщина. С другой стороны, полный
дипольный момент,
равен произведению связанного заряда
каждой грани Q'=
'S
на
расстояние d
между
ними, т. е..
где
S
— площадь
грани пластинки,
d
—
ее толщина. С другой стороны, полный
дипольный момент,
равен произведению связанного заряда
каждой грани Q'=
'S
на
расстояние d
между
ними, т. е..
![]() Таким
образом,
Таким
образом,
![]() или
или
![]()
т. е. поверхностная плотность связанных зарядов ' равна поляризованности Р.
![]() откуда
напряженность результирующего поля
внутри диэлектрика равна
откуда
напряженность результирующего поля
внутри диэлектрика равна
![]()
Безразмерная
величина
![]() называется
диэлектрической проницаемостью среды.
называется
диэлектрической проницаемостью среды.
![]() показывает, во сколько раз поле ослабляется
диэлектриком
показывает, во сколько раз поле ослабляется
диэлектриком
![]() `
`
![]() -внешнее
поле,
-внешнее
поле,
![]() `
- связь зарядов
`
- связь зарядов
![]() ;
;
![]() ;
;
![]()
![]() =>
=>
![]()
![]()
![]()
![]()
![]() где
где
![]() -
поверхностная плотность заряда.
-
поверхностная плотность заряда.
![]()
![]()
![]()
![]() -диэлектрическая
восприимчивость вещества
-диэлектрическая
восприимчивость вещества
Билет №11
Условия для векторов E и D на границе раздела диэлектриков.
Рассмотрим
связь между векторами Е и D
на границе раздела двух однородных
изотропных
диэлектриков (диэлектрические
проницаемости которых
![]() и
и
![]() )
при
отсутствии
на границе свободных зарядов. Построим
вблизи границы раздела диэлектриков 1
и
2 небольшой замкнутый прямоугольный
контур ABCDA
длины
l,
ориентировав его так,
как показано на рис
)
при
отсутствии
на границе свободных зарядов. Построим
вблизи границы раздела диэлектриков 1
и
2 небольшой замкнутый прямоугольный
контур ABCDA
длины
l,
ориентировав его так,
как показано на рис
Согласно
теореме о циркуляции вектора Е,
![]() откуда
откуда
![]() .
(знаки интегралов AB
и CD
разные, так как пути интегрирования
противоположны, а интегралы по участкам
BC
и DA
ничтожно малы). Поэтому
.
(знаки интегралов AB
и CD
разные, так как пути интегрирования
противоположны, а интегралы по участкам
BC
и DA
ничтожно малы). Поэтому
![]()
Заменив
проекции вектора Е проекциями вектора
D,
деленными на
![]() ,
получим
,
получим
![]()
На
границе раздела двух диэлектриков (рис.
137) построим прямой цилиндр ничтожно
малой высоты, одно основание которого
находится в первом диэлектрике, другое
— во втором. Основания AS
настолько малы, что в пределах каждого
из них вектор
D
одинаков. Согласно теореме Гаусса,
![]()
(нормали
n
и n'
к основаниям цилиндра направлены
противоположно). Поэтому
![]()
Заменив,
проекции вектора D
проекциями вектора E,
умноженными на
![]() ,
получим
,
получим
![]()
Таким
образом, при переходе через границу
раздела двух диэлектрических сред
тангенциальная
составляющая вектора E(![]() )
и нормальная составляющая вектора D
(
)
и нормальная составляющая вектора D
(![]() )
изменяются непрерывно (не претерпевают
скачка), а нормальная составляющая
вектора E(
)
изменяются непрерывно (не претерпевают
скачка), а нормальная составляющая
вектора E(![]() )
и тангенциальная составляющая вектора
D
(
)
и тангенциальная составляющая вектора
D
(![]() )
претерпевают скачок.
)
претерпевают скачок.
Линии
этих
векторов испытывают излом (преломляются).
Найдем связь между углами
![]() и
и
![]() (на рис
(на рис
![]() >
>![]() ).
).
![]() и
и
![]() .
.
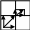
Разложим
векторы
![]() и
и
![]() у
границы раздела на тангенциальные и
нормальные составляющие. Из рис
следует, что
у
границы раздела на тангенциальные и
нормальные составляющие. Из рис
следует, что
![]() .
Учитывая
записанные выше условия, получим закон
преломления линий напряженности Е
(а значит, и линий смещения D)
.
Учитывая
записанные выше условия, получим закон
преломления линий напряженности Е
(а значит, и линий смещения D)
![]()
Эта формула показывает, что, входя в диэлектрик с большей диэлектрической проницаемостью, линии Е я D удаляются от нормали.
Билет №12
Проводники в Эл. Поле. Напряженность и потенциал внутри и на поверхности проводника. Поле вблизи поверхности проводника. Распределение зарядов в проводнике
Проводники в Эл. Поле. Напряженность и потенциал внутри и на поверхности проводника
Т.к. в проводнике имеются в достаточном количестве свободные заряды, то при помещении проводника в Эл. Поле свободные заряды перераспределяются, пока напряженность поля внутри проводника не станет равна 0.
Вывод: внутри проводников Е=0
Е на поверхности проводника = 0. Вектор Е перпендикулярен поверхности проводника.
Распределение зарядов в проводнике

![]()
![]()
![]()
на проводнике зависит от радиуса кривизны поверхности (~1/r)
Поле вблизи поверхности проводника
Выбираем замкнутую поверхность в виде цилиндр с основанием параллельным поверхности: одно основание внутри, другое снаружи.
![]()
Напряженность ~ поверхностной плотности зарядов в данной точке
Вблизи острия – стекание или натекание заряда.
Билет №13
Электроемкость уединенного проводника. Взаимная емкость двух проводников. Конденсаторы. Емкость плоского конденсатора
Электроемкость уединенного проводника
![]() С-Электроемкость
уединенного проводника
С-Электроемкость
уединенного проводника
![]() C-характеристика
проводника, не зависит не от q
не от
C-характеристика
проводника, не зависит не от q
не от
![]()
![]() [C]=Кл\В=Ф
[C]=Кл\В=Ф
Конденсаторы
Конденсатор- система, состоящая из 2х проводников (обкладок), способная принимать на себя большой заряд, при незначительном изменении U
Конденсатор состоит из двух проводников (обкладок), разделенных диэлектриком. На емкость конденсатора не должны оказывать влияния окружающие тела, поэтому проводникам придают такую форму, чтобы поле, создаваемое накапливаемыми зарядами, было сосредоточено в узком зазоре между обкладками конденсатора. Этому условию удовлетворяют 1) две плоские пластины; 2) два цилиндра; 3) две концентрические сферы. Поэтому в зависимости от формы обкладок, конденсаторы делятся на плоские, цилиндрические и сферические.
Под емкостью конденсатора понимается физическая величина, равная отношению заряда Q, накопленного в конденсаторе, к разности потенциалов между его обкладками.
Обкладки располагаются так, что приближение 3 проводника не влияет на его емкость.
C=q\U q-переносимый заряд с одной обкладки на другую
Примеры расчета емкости конденсатора
C=q\U ;
![]() ;
D=
=q\S
=>
;
D=
=q\S
=>
![]()
d =|-Edr|=U
![]()
U=![]() d
d![]()
![]()
![]()
Емкость плоского конденсатора
Рассчитаем
емкость плоского конденсатора, состоящего
из двух параллельных металлических
пластав площадью S каждая, расположенных
на расстоянии d друг от друга в имеющих
заряды +Q и —Q. Если расстояние между
пластинами мало по сравнению с их
линейными размерами, то краевыми
эффектами можно пренебречь и поле между
обкладками считать однородным. Его
можно рассчитать используя формулы
![]() и
и
![]() .
При наличии диэлектрика между обкладками
разность потенциалов между ними,
.
При наличии диэлектрика между обкладками
разность потенциалов между ними,
![]() где е — диэлектрическая проницаемость.
Заменяя Q=
S,
с учетом (94.2) получим выражение для
емкости плоского конденсатора
где е — диэлектрическая проницаемость.
Заменяя Q=
S,
с учетом (94.2) получим выражение для
емкости плоского конденсатора
![]()
Билет 14
Расчет емкости сферического и цилиндрического конденсатора
Емкость цилиндрического конденсатора


 l,
R,r,
l,
R,r,

R C=q/U
q=![]()
r ![]() x
x
![]()
-d![]()
![]()
U=-![]()
 ;
;
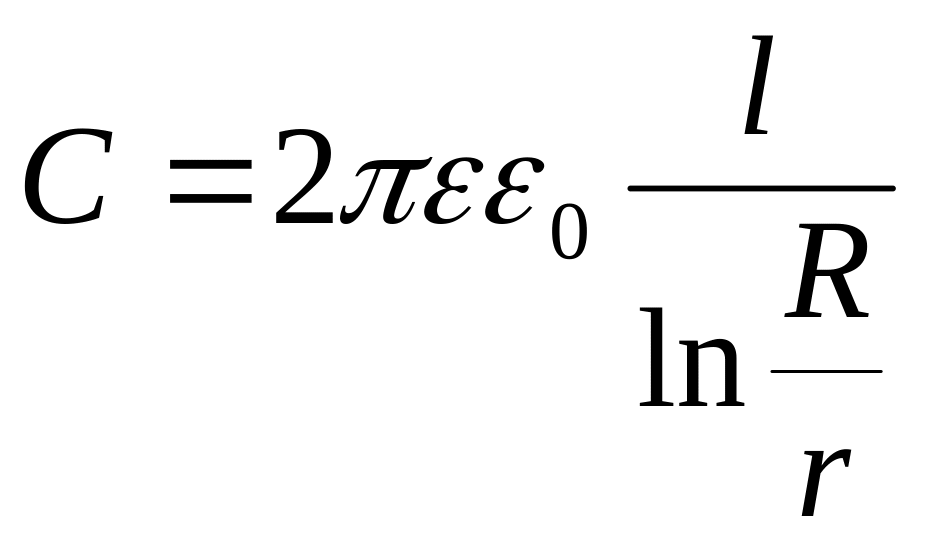
Емкость сферического конденсатора
Для
определения емкости сферического
конденсатора, состоящего из двух
концентрических обкладок, разделенных
сферическим слоем диэлектрика,
используем
формулу
 для разности потенциалов
между
двумя точками, лежащими на расстояниях
r1 и r2 (r2>r1) от центра заряженной
сферической поверхности. При наличии
диэлектрика между обкладками разность
потенциалов
для разности потенциалов
между
двумя точками, лежащими на расстояниях
r1 и r2 (r2>r1) от центра заряженной
сферической поверхности. При наличии
диэлектрика между обкладками разность
потенциалов
![]()
![]() .
Если
d=r2-r1<<r1,
то r2=R1=r
и
.
Если
d=r2-r1<<r1,
то r2=R1=r
и
![]() площадь
сферической обкладки, то получаем
формулу
.
Таким образом, при малой
величине
зазора по сравнению с радиусом выражения
для емкости сферического и плоского
конденсаторов совпадают.
площадь
сферической обкладки, то получаем
формулу
.
Таким образом, при малой
величине
зазора по сравнению с радиусом выражения
для емкости сферического и плоского
конденсаторов совпадают.
Билет №15
Энергия заряженных уединенного проводника, конденсатора и системы проводников. Энергия электростатического поля. Объемная плотность энергии. Энергия Эл. Поля.
1.
Энергия системы неподвижных точечных
зарядов.
Электростатические силы взаимодействия
консервативны, следовательно, система
зарядов обладает потенциальной
энергией. Найдем потенциальную энергию
системы двух неподвижных точечных
зарядов q1
и
q2
находящихся на расстоянии r
друг от друга. Каждый из этих зарядов в
поле другого обладает потенциальной
энергией:
![]()
![]()
где
(![]() и
и
![]() —
соответственно потенциалы, создаваемые
зарядом q2
в точке нахождения заряда q1
и зарядом Q1
в
точке нахождения заряда Q2.
—
соответственно потенциалы, создаваемые
зарядом q2
в точке нахождения заряда q1
и зарядом Q1
в
точке нахождения заряда Q2.
![]() и
и
![]() .
Поэтому W1=W2=W
и W=q1
=q2
.
Поэтому W1=W2=W
и W=q1
=q2![]() =0.5(q1
-
q2
)
=0.5(q1
-
q2
)
Добавляя
к системе из двух зарядов последовательно
заряды q3,
q4,
..., можно убедиться
в том, что в случае п
неподвижных
зарядов энергия взаимодействия системы
точечных
зарядов равна
![]()
где
![]() —
потенциал, создаваемый в той точке, где
находится заряд Qi,
всеми
зарядами, кроме i-го. .
—
потенциал, создаваемый в той точке, где
находится заряд Qi,
всеми
зарядами, кроме i-го. .
2.
Энергия заряженного уединенного
проводника.
Пусть имеется уединенный проводник,
заряд, емкость и потенциал которого
соответственно равны Q,
С,
![]() .
Увеличим
заряд
этого проводника на dQ.
Для
этого необходимо перенести заряд dQ
из
бесконечности
на уединенный проводник, затратив на
это работу, равную dA=
dQ=C
d
.
Увеличим
заряд
этого проводника на dQ.
Для
этого необходимо перенести заряд dQ
из
бесконечности
на уединенный проводник, затратив на
это работу, равную dA=
dQ=C
d
Чтобы зарядить тело от нулевого потенциала до , необходимо совершить работу
![]()
Энергия заряженного проводника равна той работе, которую необходимо совершить, чтобы зарядить этот проводник.
3.
Энергия заряженного конденсатора.
Как всякий заряженный проводник,
конденсатор
обладает энергией, которая в равна
![]()
Q
— Заряд конденсатора, С
—
его емкость,
![]() —
разность потенциалов между обкладками
конденсатора.
—
разность потенциалов между обкладками
конденсатора.
Можно найти механическую (пондеромоторную) силу, с которой пластины конденсатора притягивают друг друга. Для этого предположим, что расстояние х между пластинами меняется, например, на величину dx. To действующая сила совершает работу dA=Fdx вследствие уменьшения потенциальная энергии системы
Fdx= —dW, откуда F=-dW/dx
В
итоге,
![]()
Производя дифференцирование при конкретном значении энергии найдем искомую силу:
F=-dW/dx=-![]()
где знак минус указывает, что сила F является силой притяжения.
4
Энергия
электростатического поля.
Преобразуем формулу, выражающую энергию
плоского конденсатора посредством
зарядов и потенциалов, воспользовавшись
выражением для емкости плоского
конденсатора (![]() )
н
разности потенциалов между
его обкладками (
)
н
разности потенциалов между
его обкладками (![]() ).
Тогда
).
Тогда
![]()
где V=Sd—объем конденсатора. Формула показывает, что энергия конденсатора выражается через величину, характеризующую электростатическое поле, напряженность Е.
Объемная плотность энергии электростатического поля (энергия единицы объема)
![]()
Это
выражение справедливо только для
изотропного диэлектрика, для которого
выполнится
соотношение Р=![]()
Формулы (9S.4) и (95.7) соответственно связывают энергию конденсатора с зарядом на его обкладках и с напряженностью поля. Возникает, естественно, вопрос о локализации электростатической энергии и что является ее носителем — заряды или ноле? Ответ на этот вопрос может дать только опыт. Электростатика изучает постоянные во времени поля неподвижных зарядов, т. е. в ней поля и обусловившие их заряды неотделимы друг от друга. Поэтому электростатика ответить на поставленные вопросы не может. Дальнейшее развитие теории эксперимента показало, что переменные во времени электрические и магнитные поля могут существовать обособленно, независимо от возбудивших их зарядов, и распространяются в пространстве в виде электромагнитных волн, способных переносить энергию. Это убедительно подтверждает основное положение теории близкодействия о том, что энергия локализована в поле и что носителем энергии является поле.
Билет №16
Постоянный Эл. Ток, его характеристики (сила тока, плотность тока) и условия существования. Сторонние силы. ЭДС сторонних сил. Сопротивление проводников. Проводники, полупроводники, изоляторы и сверхпроводники. Законы Ома и Джоуля-Ленца в интегральной и дифференциальной форме
Электрическим током называется любое упорядоченное (направленное) движение электрических зарядов. В проводнике под действием приложенного электрического поля Е свободные электрические заряды перемещаются: положительные — по полю, отрицательные — против поля, т. е. в проводнике возникает электрический ток, называемый током проводимости. Если же упорядоченное движение электрических зарядов осуществляется перемещением в пространстве заряженного макроскопического тела, то возникает так называемый конвекционный ток.
Для возникновения и существования электрического тока необходимо, с одной стороны, наличие свободных носителей тока — заряженных частиц, способных перемещаться упорядоченно, а с другой — наличие электрического поля, энергия которого, каким-то образом восполняясь, расходовалась бы на их упорядоченное движение. За направление тока условно принимают направление движения положительных зарядов.
Количественной мерой электрического тока служит сила тока I — скалярная физическая величина, определяемая электрическим зарядом, проходящим через поперечное сечение проводника в единицу времени: I=dq / dt. Если сила тока и его направление не изменяются со временем, то такой ток называется постоянным. Для постоянного тока I=Q/t, где Q — электрический заряд, проходящий за время t через поперечное сечение проводника. Единица силы тока — ампер (А).
Физическая величина, определяемая силой тока, проходящего через единицу площади поперечного сечения проводника, перпендикулярного направлению тока, называется плотностью тока: j=dI/dS
Плотность тока — вектор, ориентированный по направлению тока, т. е. направление вектора j совпадает с направлением упорядоченного движения положительных зарядов. Единица плотности тока — ампер на метр в квадрате (А/м2).
Сила
тока сквозь произвольную поверхность
S
определяется
как поток вектора j,т.
е. I=![]() ,
где dS=ndS
(n-единичный
вектор нормали к площадке dS,
составляющей с вектором j
угол
,
где dS=ndS
(n-единичный
вектор нормали к площадке dS,
составляющей с вектором j
угол
![]() )
)
Сторонние силы.
Силы неэлектростатического происхождения, действующие на заряды со стороны источников тока, называются сторонними.
Природа сторонних сил может быть различной. Например, в гальванических элементах они возникают за счет энергии химических реакций между электродами и электролитами; в генераторе — за счет механической энергии вращения ротора генератора и т. п.
Сторонние
силы совершают работу по перемещению
электрических зарядов. Физическая
величина, определяемая работой,
совершаемой сторонними силами при
перемещении
единичного положительного заряда,
называется электродвижущей
силой
(э. д. с.), действующей в цепи
![]()
Сторонняя
сила F,
действующая на заряд Qo.
может быть выражена как
![]()
где
Е — напряженность поля сторонних сил.
Работа же сторонних сил по перемещению
заряда
Qo
на
замкнутом участке цепи равна
![]()
Проводники, полупроводники, изоляторы и сверхпроводники
В
зависимости от концентрации свободных
зарядов тела делятся на проводники,
диэлектрики и полупроводники.
Проводники-тела,
в которых электрический заряд может
перемещаться по всему его объему.
Проводники делятся на две группы:
1)проводники 1 рода (металлы) - перенос в
них зарядов (свободных электронов) не
сопровождается химическими превращениями.
2) проводники 2 рода (пр. расплавленные
соли, растворы кислот) – перенос в них
зарядов (положительных и отрицательных
ионов) ведет к химическим изменениям.
![]() .
При увел. T,
увеличивается R.
.
При увел. T,
увеличивается R.
Диэлектрики (например, стекло, пластмассы) – тела, в которых практически отсутствуют свободные заряды.
Полупроводники
(пр. германий, кремний) занимают
промежуточное положение между проводниками
и диэлектриками. Указанное деление тел
является весьма условным, однако большое
различие в них концентраций свободных
зарядов обусловливает огромные
качественные различия в их поведении
и оправдывает, поэтому деление тел на
проводники, диэлектрики и полупроводники.
При увел. T,
уменьшается R.
![]()
Сверхпроводники. Сопротивление металлов (например, Al, Pb, Zn и др.) и их сплавов при очень низких температурах, называемых критическими, характерных для каждого вещества, скачкообразно уменьшается до нуля, т. е. металл становится абсолютным проводником. Это явление, названо сверхпроводимостью. Практическое использование сверхпроводимых металлов затруднено из-за их низких критических температур. В наше время обнаружены и активно исследуются керамические материалы, обладающие сверхпроводимостью при температуре выше 100 К.
Сопротивление проводников
Немецкий физик Г. Ом экспериментально установил, что сила тока I, текущего проводнику, пропорциональна напряжению U на концах проводника: I=U/R
где R — электрическое сопротивление проводника. Это уравнение выражает закон Ома для участка цепи (не содержащего источника тока): сала тока в проводнике прямо пропорциональна приложенному напряжению и обратно пропорциональна сопротивлению проводника. Единица сопротивления — ом (Ом). 1Ом — сопротивление такого проводника, в котором при напряжении 1В течет постоянный ток 1 А.
Величина G=1/R называется электрической проводимостью проводника. Единица проводимости — сименс (См): 1 См — проводимость участка электрической цепи сопротивлением 1 Ом. Сопротивление проводников зависит от его размеров и формы, а также от материала, из которого проводник изготовлен. Для однородного линейного проводника сопротивление R прямо пропорционально его длине / и обратно пропорционально площади его поперечного сечения S: R=pl/S
где р — коэффициент пропорциональности, характеризующий материал проводника и называемый удельным электрическим сопротивлением. Единица удельного электрического сопротивления — Ом метр (Ом • м). Наименьшим удельным сопротивлением обладают серебро (1,6 -10-8 Ом-м) и медь (1,7-10-8 Ом-м).
Закон Ома в дифференциальной форме
Подставив выражение для сопротивления R=pl/S в закон Ома I=U/R, получим
I/S=U/pl,
где величина, обратная удельному
сопротивлению,
![]() называется удельной электрической
проводимостью вещества проводника. Ее
единица
— сименс на метр (См/м).
называется удельной электрической
проводимостью вещества проводника. Ее
единица
— сименс на метр (См/м).
Учитывая,
что U/l=E
– напряженность электрического поля
в проводнике, I/S=j
– плотность тока, формулу I/S=U/pl
можно записать в виде j=
![]() E
E
j= E – это выражение – закон Ома в дифференциальной форме. Плотность тока в любой точке пространства пропорциональна напряженности поля в этой точке. (если поля не слишком большие).
J=![]()
Закон Ома в интегральной форме
Умножим
скалярно на dl
:
![]()
![]() ;
;
![]()
![]()
 -закон
Ома для неоднородного участка
-закон
Ома для неоднородного участка
Для
однородного
=0
=> ![]() Для
замкнутой(
=0):
Для
замкнутой(
=0):
![]()
Закон Джоуля-Ленца в дифференциальной форме
Рассмотрим однородный проводник, к концам которого приложено напряжение U.За время dt через сечение проводника переносится заряд dq=Idt. Так как ток представляет
собой перемещение заряда dq под действием электрического поля, то работа тока dA=Udq=IUdt
Если
сопротивление проводника R,
то, используя закон Ома, получим
dA=![]()
Если ток проходит по неподвижному металлическому проводнику, то вся работа тока идет на его нагревание и, по закону сохранения энергии dq=dA. Таким образом dq=IUdt=
Это выражение представляет собой закон Джоуля-Ленца.
Выделим
в проводнике элементарный цилиндрический
объем dV=dSdl(ось
цилиндра совпадает с направлением
тока), сопротивление которого
![]() .
По закону Джоуля-Ленца, за время dt
в этом объеме выделится теплота
.
По закону Джоуля-Ленца, за время dt
в этом объеме выделится теплота
![]()
Количество
теплоты, выделяющееся за единицу времени
в единице объема, называется удельной
тепловой мощностью тока. Она равна:
![]()
Используя дифференциальную форму закона Ома и соотношение p=1/y, получим
![]()
Формулы
и
![]() называют
законом
Джоуля-Ленца в дифференциальной форме.
называют
законом
Джоуля-Ленца в дифференциальной форме.
Билет №17
Классическая электронная теория электропроводности металлов и ее опытные обоснования. Вывод законов Ома и Джоуля-Ленца из электронных представлений. Закон Видемана-Франца. Затруднения классической теории электропроводности металлов.
Носителями тока в металлах являются свободные электроны (Первый из таких опытов, подтверждающих то, что электрон – носитель заряда—опыт Рикке, в котором в течение года электрический ток пропускался через три последовательно соединенных с тщательно отшлифованными торцами металлических цилиндра (Сu, Аl, Сu) одинакового радиуса. Несмотря на то что общий заряд, прошедший через эти цилиндры, достигал огромного значения (3,5-10+6 Кл), никаких, даже микроскопических, следов переноса не обнаружилось. Это явилось экспериментальным доказательством того, что ионы в металлах не участвуют в переносе электричества, а перенос заряда в металле осуществляется частицами, которые являются общими для всех металлов.)
2) Свободные электроны ведут себя как идеальный электронный газ. (По теории Друде — Лоренца, электроны обладают такой же энергией теплового движения, как и молекулы одноатомного газа. Поэтому, применяя выводы молекулярно-кинетической теории, можно найти среднюю скорость
теплового
движения электронов
![]() ,
которая для T=300K
равна 1.1*10+5 м/с. Это скорость теплового
движения электронов, которое является
хаотическим, не может привести к
возникновению тока.
,
которая для T=300K
равна 1.1*10+5 м/с. Это скорость теплового
движения электронов, которое является
хаотическим, не может привести к
возникновению тока.
При наложении внешнего электрического поля на металлический проводник кроме теплового движения электронов возникает их упорядоченное движение, т. е. возникает электрический ток. Среднюю скорость <V> упорядоченного движения электронов можно оценить согласно формуле для плотности тока: j= ne<V>.
<V><<<U>, т.е. даже при очень больших плотностях тока средняя скорость упорядоченного движения электронов, обусловливающего электрический ток, значительно меньше их скорости теплового движения. Поэтому при вычислениях результирующую скорость (<V>+<U>) можно заменять скоростью теплового движения <U>.
Закон Ома.
Пусть в металлическом проводнике существует электрическое поле. Напряженностью E= const. Co стороны поля заряд е испытывает действие силы F=eE
и приобретает ускорение a=F/m=eE/m. Таким образом, во время свободного пробега электроны движутся равноускоренно, приобретая к концу свободного пробега скорость
![]()
где <t> — среднее время между двумя последовательными соударениями с ионами решетки.
Согласно теории Друде, в конце свободного пробега электрон, сталкиваясь с ионами решетки, отдает им накопленную в поле энергию, поэтому скорость его упорядоченного движения становится равной нулю. Следовательно, средняя скорость направленного движения электрона
![]()
Классическая теория металлов не учитывает распределения электронов по скоростям, поэтому среднее время <t> свободного пробега определяется средней длиной свободного пробега <l> и средней скоростью движения электронов относительно кристаллической решетки проводника, равной <U>+<V> (<U>— средняя скорость теплового движения электронов). <V><<<U>, поэтому <t>=<l>/<U>
<V>=eE<l>/(2m<U>)
Плотность тока в металлическом проводнике,
![]()
откуда видно, что плотность тока пропорциональна напряженности поля,
т.
е. получи ли
закон Ома в дифференциальной форме.![]()
Закон Джоуля-Ленца
К концу свободного пробега электрон под действием поля приобретает дополнительную кинетическую энергию .
![]()
При соударении электрона с ионом эта энергия полностью передается решетке и идет на увеличение внутренней энергии металла, т. е. на его нагревание.
За единицу времени электрон испытывает с узлами решетки в среднем <z> столкновений: <z>=<U>/<l>
Если
п
—
концентрация электронов, то в единицу
времени происходит n<z>
столкновений
и решетке передается энергия w=n<z><E>,
которая
идет на нагревание проводника. Таким
образом энергию, передаваемую решетке
в единице объема проводника за единицу
времени
![]()
Величина w является удельной тепловой мощностью тока. Коэффициент
пропорциональности
между w
в
![]() по есть удельная проводимость у;
следовательно,
выражение
— закон Джоуля — Ленца в дифференциальной
форме.
по есть удельная проводимость у;
следовательно,
выражение
— закон Джоуля — Ленца в дифференциальной
форме.
Закон Видемана-Франца
Видеманом
и Францем экспериментально установлен
закон, согласно
которому
отношение теплопроводности (![]() )
к удельной проводимости (у)
для
всех металлов
при одной и той же температуре одинаково
и увеличивается пропорционально
термодинамической температуре.
)
к удельной проводимости (у)
для
всех металлов
при одной и той же температуре одинаково
и увеличивается пропорционально
термодинамической температуре.
![]() ,
где
,
где
![]() -постоянная,
зависящая от рода металла.
-постоянная,
зависящая от рода металла.
Элементарная
классическая теория электропроводности
металлов позволила найти значение![]() ,
где k
- постоянная Больцмана. Это значение
хорошо согласуется
с опытными данными. Однако, как оказалось
впоследствии, это согласие теоретического
значения с опытным случайно; Лоренц,
применив к электронному газу
статистику Максвелла — Больцмана, учтя
тем самым распределение электронов
скоростям,
получил,
,
где k
- постоянная Больцмана. Это значение
хорошо согласуется
с опытными данными. Однако, как оказалось
впоследствии, это согласие теоретического
значения с опытным случайно; Лоренц,
применив к электронному газу
статистику Максвелла — Больцмана, учтя
тем самым распределение электронов
скоростям,
получил,
![]() что
привело к резкому расхождению теории
c
опытом.
Таким
образом, классическая теория
электропроводности металлов объяснила
законы Ома
и Джоуля — Ленца, а также дала качественное
объяснение закона Видемана —
Франца. Однако она помимо рассмотренных
противоречий в законе Видемана-
Франца столкнулась еще с рядом трудностей
при объяснении различных опытных данных.
что
привело к резкому расхождению теории
c
опытом.
Таким
образом, классическая теория
электропроводности металлов объяснила
законы Ома
и Джоуля — Ленца, а также дала качественное
объяснение закона Видемана —
Франца. Однако она помимо рассмотренных
противоречий в законе Видемана-
Франца столкнулась еще с рядом трудностей
при объяснении различных опытных данных.
Рассмотрим некоторые из них.
Температурим
зависимость сопротивления.
Из формулы удельной проводимости
следует,
что сопротивление металлов, т. е. величина,
обратно пропорциональная у,
должна
возрастать пропорционально
![]() Этот
вывод электронной теории противоречит
опытным данным,
согласно
которым R~
T.
Этот
вывод электронной теории противоречит
опытным данным,
согласно
которым R~
T.
Оценка средней длины свободного пробега электронов в металле. Чтобы получить у, совпадающие с опытными значениями, надо принимать </> значительно больше истинных, другими словами, предполагать, что электрон проходит без соударений с ионами решетки сотни междоузельных расстояний, что не согласуется с теорией Друде — Лоренца.
Теплоемкость металлов. Теплоемкость металла складывается из теплоемкости его кристаллической решетки и теплоемкости электронного газа. Поэтому атомная (т. е. на 1 моль) теплоемкость металла должна быть значительно большей. Наличие электронов проводимости не сказывается на значении теплоемкости, что не объясняется классической электронной теорией.
Указанные расхождения теории с опытом можно объяснить тем, что движение в металлах подчиняется не законам классической механики, а законам квантовой механики и, следовательно, поведение электронов проводимости надо описывать не статистикой Максвелла-Больцмана, а квантовой статистикой.
Недостатки классической электронной теории
1) Учет распределения скоростей электронов (по Максвелу) приводит к худшему согласованию с экспериментальными результатами.
2) Температурная зависимость электропроводности металлов не совпадает с экспериментальной
Теория:
![]()
Эксперимент:
![]()
3) Чтобы получить численное совпадение для в теории с экспериментом, надо считать, что составляет примерно 100 межатомных расстояний.
4) Вопрос о теплоемкости
Согласно МКТ: C=6/2R+3/2R у металлов больше
C=6/2R у неметаллов (т.к. нет электрического газа)
Малярная теплоемкость всех твердых тел одинакова n=6/2R
Вывод: Классическая теория электропроводности многого не учитывает
Тема №18
Магнитное поле. Вектор магнитной индукции. Опыт Эрстеда. Магнитный поток. Теорема Остроградского-Гаусса. Магнитный момент контура с током. Графическое изображение магнитных полей.
В 1821 году Эрстед обнаружил магнитное поле вокруг проводника с током. Важнейшая особенность магнитного поля состоит в том, что, оно действует только на движущиеся в этом поле электрические заряды.
За направление магнитного поля в данной точке принимается направление, вдоль которого располагается положительная нормаль к рамке. За направление магнитного поля может быть также принято направление, совпадающее с направлением силы, которая действует на северный полюс магнитной стрелки, помещенной в данную точку. Так как оба полюса магнитной стрелки лежат в близких точках поля, то силы, действующие на оба полюса, равны друг другу. Следовательно, на магнитную стрелку действует пара сил, поворачивающих ее так, чтобы ось стрелки, соединяющая южный полюс с северным, совпадала с направлением поля.
Основная характеристика контура – магнитный момент.
Pm=ISn где S— площадь поверхности контура (рамки), n — единичный вектор нормали к поверхности рамки. Направление Рm совпадает, таким образом, с направлением положительной нормали.
Вращающий момент M=[PmB](B – вектор магнитной индукции, Pm – вектор магнитного момента рамки)
Если
в данную точку магнитного поля помещать
рамки с различными магнитными моментами,
то на них действуют различные вращающие
моменты, однако отношение
![]() (
(
![]() — максимальный
вращающий момент) для всех контуров
одно и то же и
поэтому может служить характеристикой
магнитного поля, .называемой магнитной
индукцией:
И=
— максимальный
вращающий момент) для всех контуров
одно и то же и
поэтому может служить характеристикой
магнитного поля, .называемой магнитной
индукцией:
И=
Линии магнитной индукции – линии, касательные к которым в каждой точке совпадают с направлением вектора В.
Их направление задается правилом винта: головка винта, ввинчиваемого по направлению тока, вращается в направлении линий магнитной индукции.
Линии магнитной индукции можно проявить с помощью железных опилок, намагничивающихся в исследуемом поле и ведущих себя подобно маленьким магнитным стрелкам.
Линии магнитной индукции всегда замкнуты и охватывают проводники с током.
Магнитное поле макротоков описывается вектором напряженности Н. Для однородной изотропной среды вектор магнитной индукции связан с вектором напряженности следующим соотношением:
![]() ,
где
,
где
![]() -
магнитная постоянная,
-
магнитная постоянная,
![]() -
безразмерная величина – магнитная
проницаемость среды, показывающая, во
сколько раз магнитное поле макротоков
Н усиливается за счет поля микротоков.
-
безразмерная величина – магнитная
проницаемость среды, показывающая, во
сколько раз магнитное поле макротоков
Н усиливается за счет поля микротоков.
19. Магнитное поле и его характеристики
Опыт показывает, что, подобно тому, как в пространстве, окружающем.электрические заряды, возникает электростатическое поле, так и в пространстве, окружающем токи и постоянные магниты, возникает силовое поле, называемое магнитным. Наличие магнитного поля обнаруживается по силовому действию на внесенные в него проводники с током или постоянные магниты. Название «магнитное поле» связывают с ориентацией магнитной стрелки под действием поля, создаваемого током (это явление впервые обнаружено датским физиком X. Эрстедом (1777—1851)).
Электрическое поле действует как на неподвижные, так и на движущиеся в нем электрические заряды. Важнейшая.особенность магнитного поля состоит в том, что оно действует только на движущиеся в этом поле электрические заряды. Опыт показывает, что характер воздействия магнитного поля на ток различен в зависимости от формы проводника, по которому течет ток, от расположения проводника и от направления тока. Следовательно, чтобы охарактеризовать магнитное поле, надо рассмотреть его действие на определенный ток.
Подобно тому, как при исследовании электростатического поля использовались точечные заряды, при исследовании магнитного поля используется замкнутый плоский контур с током (рамка с током), линейные размеры которого малы по сравнению с расстоянием до токов, образующих магнитное поле. Ориентация контура в пространстве определяется направлением нормали к контуру. Направление нормали определяется правилом правого винта: за положительное направление нормали принимается направление поступательного движения винта, головка которого вращается в направ' лении тока, текущего в рамке .
Опыты показывают, что магнитное поле оказывает на рамку с током ориентирующие действие.
Этот результат используется для выбора направления магнитного поля. За направление магнитного поля в данной точке принимается направление, вдоль которого располагается положительная нормаль к рамке. За направление магнитного поля может быть также принято направление, совпадающее с направлением силы, которая действует на север-вый полюс магнитной стрелки, помещенной в данную точку/ Так как оба полюса магнитной стрелки лежат в близких точках поля, то силы, действующие на оба полюса, равны друг другу. Следовательно, на магнитную стрелку действует пара сил, поворачивающая ее так, чтобы ось стрелки, соединяющая южный полюс с северным, совпадала с направлением поля.
Рамкой с током можно воспользоваться также и для количественного описания магнитного поля. Так как рамка с током испытывает ориентирующее действие поля, то на нее в магнитном поле действует пара сил. Вращающий момент сил зависит как от свойств поля в данной точке, так и от свойств рамки и определяется формулой М=[ pm B]
где pm — вектор магнитного момента рамки с током (В — вектор магнитной индукции,
количественная характеристика магнитного поля). Для плоского контура с током I pm=ISn,
где S- площадь поверхности контура (рамки), n - единичный вектор нормали к поверхности рамки. Направление pm совпадает, таким образом, с направлением положительной нормали.
Если в данную точку магнитного поля помещать рамки с различными магнитными моментами, то на них действуют различные вращающие моменты, однако отношение ММАХ / pm (ММАХ — максимальный вращающий момент) для всех контуров одно и то же и поэтому может служить характеристикой магнитного поля, называемой магнитной индукцией: B= ММАХ / pm .
Магнитная индукция в данной точке однородного магнитного поля определяется максимальным вращающим моментом, действующим на рамку с магнитным моментом, равным единице, когда нормаль к рамке перпендикулярна направлению поля. Следует отметить, что вектор В может быть выведен также из закона Ампера и из выражения для силы Лоренца .
Так как магнитное поле является силовым, то его, по аналогии с электрическим, изображают с помощью линий магнитной индукции — линий, касательные к которым в каждой точке совпадают с направлением вектора В. Их направление задается правилом правого винта: головка винта, ввинчиваемого по направлению тока, вращается в направлении линий магнитной индукции.
Линии магнитной индукции можно «проявить» с помощью железных опилок, намагничивающихся в исследуемом поле и ведущих себя подобно маленьким магнитным стрелкам. Линии магнитной индукции всегда замкнуты и охватывают проводники с током. Этим они отличаются от линий напряженности электростатического поля, которые являются разомкнутыми (начинаются на положительных зарядах и кончаются на отрицательных .
Опыты показали, что, разрезая магнит на части, его полюсы разделить нельзя, т. е. в отличие от электрических зарядов свободные магнитные «заряды» не существуют, поэтому линии магнитной индукции не могут обрываться на полюсах. В дальнейшем было установлено, что внутри полосовых магнитов имеется магнитное поле, аналогичное полю внутри соленоида, и линии магнитной индукции этого магнитного поля являются продолжением линий магнитной индукции вне магнита. Таким образом, линии магнитной индукции магнитного поля постоянных магнитов являются также замкнутыми.
До сих пор мы рассматривали макроскопические токи, текущие в проводниках. Однако, согласно предположению французского физика А. Ампера (1775—1836), в любом теле существуют микроскопические токи, обусловленные движением электронов в атомах и молекулах. Эти микроскопические молекулярные токи создают свое магнитное поле и могут поворачиваться в магнитных полях макротоков. Например, если вблизи какого-то тела поместить проводник с током (макроток), то под действием его магнитного поля микротоки во всех атомах определенным образом ориентируются, создавая в теле дополнительное магнитное поле. Вектор магнитной индукции В характеризует результирующее магнитное поле, создаваемое всеми макро- и микротоками, т. е. при одном и том же токе и прочих равных условиях вектор В в различных средах будет иметь разные значения.
Магнитное поле макротоков описывается вектором напряженности Н. Для однородной изотропной среды вектор магнитной индукции связан с вектором напряженности следующим соотношением:
B=μ0μH,
где μо — магнитная постоянная, μ - безразмерная величина — магнитная проницаемость среды, показывающая, во сколько раз магнитное поле макротоков Н усиливается за счет поля микротоков среды.
Сравнивая векторные характеристики электростатического (Е и D) и магнитного (В и Н) полей, укажем, что аналогом вектора напряженности электростатического поля Е является вектор магнитной индукции В, так как векторы Е и В определяют силовые действия этих полей и зависят от свойств среды. Аналогом вектора электрического смещения D является вектор напряженности Н магнитного поля.
Магнитное поле постоянных токов различной формы изучалось французскими учеными Ж. Био (1774—1862) и Ф. Саваром (1791—1841). Результаты этих опытов были обобщены выдающимся французским математиком и физиком д. Лапласом.
Закон Био-Савара-Лапласа для проводника с током І, элемент dl которого создает в некоторой точке A (рис. 164) индукцию поля dB, записывается в виде dB=
где dl- вектор, по модулю равный длине dl элемента проводника и совпадающий по направлению с током, г -радиус-вектор, проведенный из элемента dl проводника в точку А поля, r — модуль радиуса-вектора г. Направление dB перпендикулярно dl и r, т. е. перпендикулярно плоскости, в которой они лежат, и совпадает с касательной к линии магнитной индукции. Это направление может быть найдено по правилу нахождения линий магнитной индукции (правилу правого винта): направление вращения головки винта дает направление dB, если поступательное движение винта соответствует направлению тока в элементе.
Модуль
вектора dB
определяется выражением dB=μμ0
Idl
sinα/![]()

где ά — угол между векторами dl и г.
Для магнитного поля, как и для электрического, справедлив принцип суперпозиции: магнитная индукция результирующего поля, создаваемого несколькими токами или движущимися зарядами, равна векторной сумме магнитных индукций складываемых полей, создаваемых каждым током или движущимся зарядом в отдельности:
В= ∑Вi
Расчет характеристик магнитного поля (В и Н) по приведенным формулам в общем случае сложен. Однако если распределение тока имеет определенную симметрию, то применение закона Био - Савара — Лапласа совместно с принципом суперпозиции позволяет просто рассчитать конкретные поля. Рассмотрим два примера.
1. Магннтное поле прямого тока — тока, текущего по тонкому прямому проводу бесконечной длины (рис. 165). В произвольной точке А, удаленной от оси проводника на расстояние R ,векторы dB от всех элементов тока имеют одинаковое направление

перпендикулярное плоскости чертежа («к нам»). Поэтому сложение векторов dB можно заменить сложением их модулей. В качестве постоянной интегрирования выберем угол а (угол между векторами dl и г), выразив через него все остальные величины. Из рис. 165 следует, что
r=R/sinα , dl=rdα/sinα
(радиус дуги CD вследствие малости dl равен г, и угол FDC по этой же причине можно считать прямым). Подставив эти выражения в (110.2), получим, что магнитная индукция, создаваемая одним элементом проводника, равна dB=μ0μIsinαdα/4πR. Так как угол ά для всех элементов прямого тока изменяется в пределах от 0 до π, то согласно (110.3) и (110.4), B=∫dB=μ0μI/4πR∫sinαdα= μ0μI/2πR
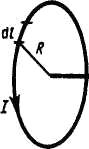
2. Магнитное поле в центре кругового проводника с током (рис. 166). Как следует из рисунка, все элементы кругового проводника с током создают в центре магнитные поля одинакового направления вдоль нормали от витка. Поэтому сложение векторов dB можно заменить сложением их модулей. Так как все элементы проводника перпендикулярны радиусу-вектору (sin ά=l) и расстояние всех элементов проводника до центра кругового тока одинаково и равно R, то, согласно (110.2),
Тогда B=∫dB=(μμ/4π)*(І/R)*∫dl=. μ0μI/2R