11.2. Оценивание ковариационной функции

Как уже упоминалось, существует несколько эмпирических схем оценивания ковариационной функции, несущественно отличающихся друг от друга. При оценке ковариационных функций будем считать процессы стационарными со средней величиной равной

E(Y_i)=0. (68)

Если это не так, то вместо величин Y_i будем рассматривать значения , сохраняя для них старое обозначение Y_i и предполагая, что число N достаточно велико и дисперсия пренебрежимо мала.

Рассмотрим простейшую схему, обеспечивающую достаточную точность в большинстве прикладных задач.

Оценку величины будем определять по формуле

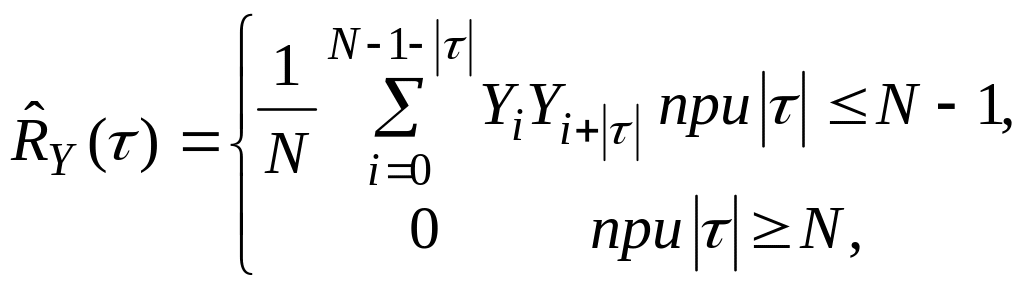(69)

где N – число членов ряда.

Найдем математическое ожидание величины (τ = 0, 1, … N– 1). Из (69) имеем

, (70)

т. е. оценка смещена. Однако при N→ ∞, что указывает на асимптотическую несмещенность.

При больших N и малых значениях τ величина смещения имеет порядок 1/N и, как правило, пренебрежимо мала. С ростом τ смещение стремится к нулю.

Помимо оценки, производимой с помощью формулы (69), используют еще другую численную схему для оценивания кова­риационной функции. Эта оценка имеет вид

(71)

Аналогично (70) для оценки (71) можно записать

. (72)

Таким образом, в отличие от (70) оценка (71) является не смещенной. Для того чтобы сравнение оценок (69) и (71) было более полным, нужно сравнить еще их среднеквадратические ошибки. Согласно (69) среднеквадратическая ошибка определяется выражением

(73)

Поскольку для оценки смещение равно нулю, то для этой оценки среднеквадратическая ошибка определяется следующим образом

. (74)

Если предположить, что случайный процесс имеет ковариационную функцию вида , то можно получить количественные оценки для среднеквадратической ошибки оценок ковариации (69) и (71). Расчеты показывают, что поведение средних квадратических ошибок при увеличении N различно. Среднеквадратическая ошибка оценки (69) уменьшается, в то время как для другой оценки (71) эта величина имеет тен­денцию к увеличению. Следовательно, несмотря на то, что оценка (69) является асимптотически смещенной, а (71)—не смещенной, ее использование более целесообразно, чем оценки (71), так как среднеквадратическая ошибка оценки в этом случае уменьшается.

11.3. Об оценивании пространственных ковариационных функций

Рассмотренные схемы оценивания ковариационных функций применяются в случае, если случайная величина является функцией одной переменной. Эти численные схемы можно обобщить тогда, когда рассматривается не случайная функция, а случайное поле.

Рассмотрим поле случайной величины . Для оценивания пространственной ковариационной функции этого поля применяется следующая схема

, (75)

где — реализация случайного поля.

Из формулы (75) следует, что эта оценка является не сме­щенной. В том случае, когда поле является однородным и изотропным, схема (75) принимает вид

, (76)

где .

Эта оценка также не смещенная.

Оценим теперь дисперсию ковариации. С учетом введенных обозначений можно записать

. (77)

Если считать, что реализации являются статистически независимыми, а распределение случайной величины — нормальным, то, полагая i = р, получим следующее выражение для дисперсий оценки ковариационной функции

. (78)

Пользуясь формулой (78), можно получить формулу для оценки структурной функции. Она имеет вид

. (79)

Заметим, что если коррелированность реализаций оказывается существенной, т. е. их нельзя считать независимыми, то оценки по формулам (78) и (79) завышают точность структурных и ковариационных функций.

Если площадь территории, для которой рассчитывается ковариационная функция, оказывается не очень большой, а число пунктов наблюдений достаточно велико (примерно 50—60), то дисперсию оценки ковариации можно приближенно оценить при помощи следующего выражения

, (80)

где — линейный масштаб территории; — дисперсия, определяемая по формуле (78) при фиксированных значе­ниях j и k; A — множитель, зависящий от вида корреляционной функции. В частности, для корреляционной функции , А = 0,67.