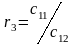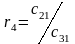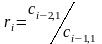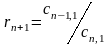8. Критерий Льенара

При выполнении условия 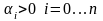для устойчивости системы необходимо и достаточно, чтобы были положительными или все определители Гурвица с четными индексами, или все определители Гурвица с нечетными индексами. Следовательно, чтобы система была устойчивой необходимо и достаточно, чтобы

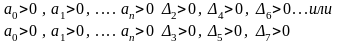
Пример. Имеется характеристическое уравнение.

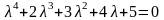
(Необходимое условие a₀>0, a₁=2>0, a₂=3>0, a₃=4>0, a₄=5>0).

Согласно критерию необходимо и достаточно 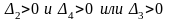Проверим выполнение более простого второго условия.

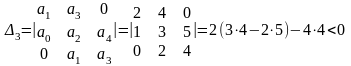
Система не устойчива.

9. Критерий устойчивости Рауса

Применение критерия требует составления таблицы Рауса. Элементами её первой строки являются четные коэффициенты характеристического уравнения, начиная с a₀,a₂ a₄, …

Элементы последующих строк вычисляют по приведенным в таблице формулам. Причем при вычислении элементов какой-либо i-ой строки необходимо предварительно вычислить коэффициент ri. Всего в таблице заполняют n+1 строк.

Критерий формируют следующим образом: система устойчива, если все элементы первого столбца таблицы Рауса имеют одинаковый знак. Обычно характеристическое уравнение приводится к виду a₀>0, тогда все элементы первого столбца должны быть положительными. C_i,1>0, i=2 ,n+1.

При наличии отрицательных элементов в первом столбце таблицы Рауса местами неустойчивы. Если один из элементов первого столбца равен 0, то системы на границе устойчивости характеристического уравнения имеют пару чисто мнимых корней.

При равенстве нулю последнего n+1 элемента или отрицательного элемента на первом столбце. Так как при таких условиях система находится на границе устойчивости или неустойчивости.

Составляя таблицу Рауса, расчет можно закончить при появлении первого нулевого или отрицательного элемента на первом столбце, т.к. система на границе устойчива или неустойчива.

Вспомогательные коэффициенты	№ строки	№ столбца
		1	2	3
-	1	C11=a0	C21=a2	C13=a4
-	2	C21=a1	C22=a3	C23=a5
	3	C31=C12+ r3C22	C32=C13+ r3C23	C33= C14+ r3C24
	4	C41=C22+ r4C32	C42=C23+ r4C33	C43= C24+ r4C34
-----	-----	-----	-----	-----
	i	Ci1= Ci-2,2+ riCi-1,2	Ci2= Ci-2,3+ riCi-1,3	Ci3= Ci-2,4+ riCi-1,3
	n+1	Ci,n+1= Cn-1,-2+ rn+1Cn,2	-	-

10. Вопросы

1. Какое значение имеет устойчивость в теории САУ?

2. Какое звено является устойчивым по входу?

3. Как формулируется достаточное условие устойчивости?

4. Какие критерии устойчивости являются алгебраическими?

5. В чем суть критерия устойчивости Гурвица?

6. В чем суть критерия устойчивости Льенара?

7. В чем суть критерия устойчивости Рауса?