7. Вопросы

1. В чем заключается принцип суперпозиции?

2. Для чего используются передаточные функции системы?

3. Перечислите частотные функции?

4. В чем физический смысл функции Грина?

5. В чем отличие Логарифмических частотных характеристик, от частотных.

2. Лекция №9 Устойчивость линейных стационарных систем

   1. Понятие устойчивости

Устойчивость является одним из основных требований, предъявляемых к системам автоматического управления (САУ). Неустойчивые САУ неработоспособны, поэтому важно уметь определять и соответствующий выбор структуры и параметры системы, обеспечить её устойчивость. В системе управления требуется поддерживать некоторое заданное движение, которое называется невозмущенным движением.

Вследствие различных возмущающих воздействий фактическое движение отличается от невозмущенного движения. В нормально функционирующей системе отклонение фактического движения от невозмущенного движения должно быть небольшим, а это возможно лишь в устойчивых системах.

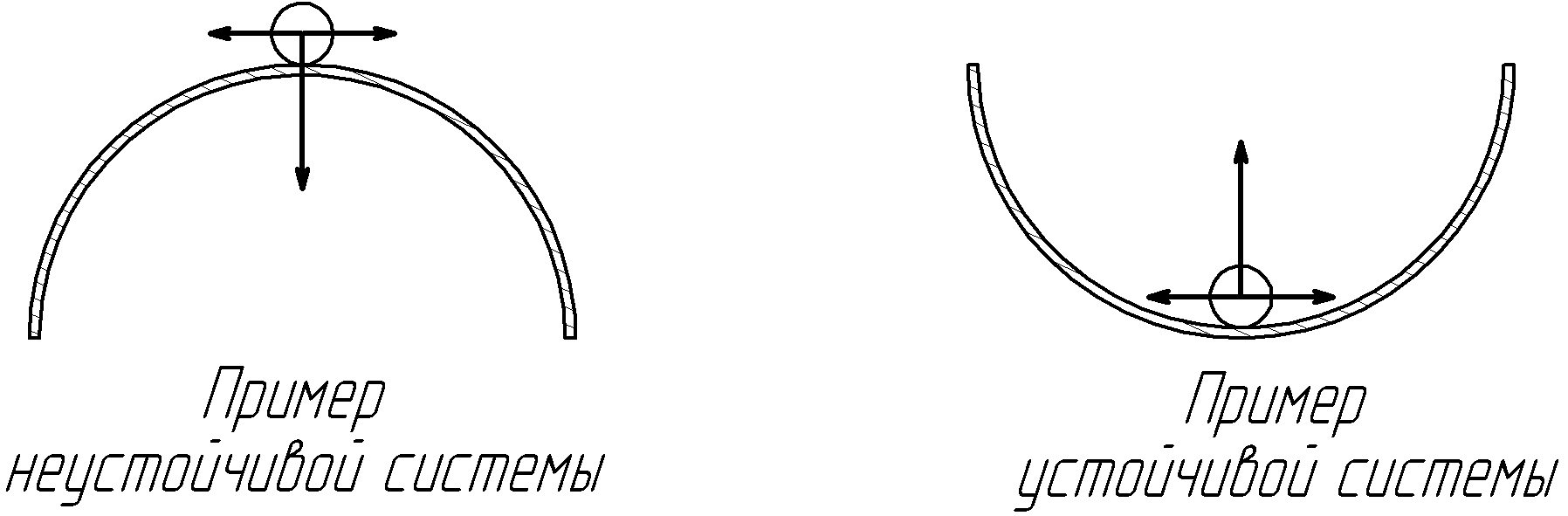
2. Устойчивость по входу

Звено называется устойчивым по входу (осуществляющим устойчивое преобразование вход-выход), если при любом ограниченном входном воздействии x(t) и нулевых начальных условиях, выходная реакция y(t) является ограниченной при любом конечном 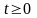и при 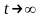и называется неустойчивым на входе в противном случае.

Об устойчивости по входу можно судить по свойствам весовой функции

Теорема 4.1 Для того, чтобы звено, описываемое операторным уравнением, было устойчиво по входу, необходимо и достаточно выполнение условия .

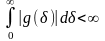Доказательство: известно, что вход и выход звена осуществляются по формуле.

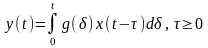
Пусть x(t) – произвольно правильная функция, т.е. такая, что

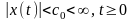
Где С₀ – некоторая константа. Тогда

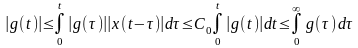
3. Характеристическое уравнение

Устойчивость линейной системы зависит от её характеристического уравнения.

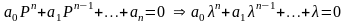
Где дифференциальный параметр собственный

P рассматривается, как переменная. Левая часть характеристического уравнения называется характеристическим полиномом.

Характеристический полином системы совпадает с её собственным оператором или знаменателем передаточной функции.

4. Необходимое и достаточное условие устойчивости

Для того чтобы линейная непрерывная система была устойчива, необходимо и достаточно, чтобы все корни её характеристического уравнения

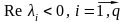
Или другая формулировка.

Для того чтобы линейная непрерывная система была устойчивой, необходимо и достаточно, чтобы все корни её характеристического уравнения были левыми, т.е. располагались в левой полуплоскости.

1) ;

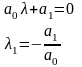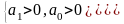
2)

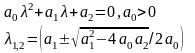
5. Условие строгой реализуемости передаточной функции

Многочлен Q(P) (характеристический многочлен звена) не имеет других корней, кроме корней с отрицательными вещественными частями (условие устойчивости характеристического многочлена).

Пример.

1. Идеальный усилитель Q(P)=1 и корней нет.

2. Интегратор Q(P)=P и один вещественный корень 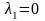система будет неустойчива.

3. Апериодическое звено Q(P)=TP+1 и один вещественный корень 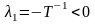при Т>0 система будет устойчива.

4. Колебательное звено 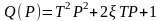и имеется два комплексно -сопряженных корня, 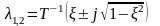причем вещественная часть отрицательна 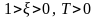система устойчива.

Эти звенья являются устойчивыми по входу, за исключением интегратора. Переходная функция неограниченно растет, хотя является реакцией на единичное воздействие 1(t).