Метод Гринберга.
Искомую функцию можно представить разложением по собственным функциям соответствующей задачи Штурма-Лиувилля:
;
.
А коэффициенты находим по известной формуле:
.
Задача Дирихле для прямоугольника
Задача Штурма-Лиувилля:
;
и
.
Получим
.
Преобразуем:
.
Учитывая
получим:
;
можем представить в виде
Если граничные условия имеют конкретный вид:
;
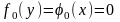
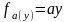
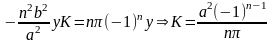
Подставим граничные условия и получим:
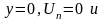
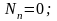
и
,
тогда
если
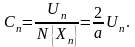
Получаем
итого
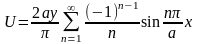
Теперь пусть
тогда
получим
.
Учитывая граничные условия:
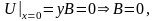
Решим ту же задачу используя искусственный приём:
,
;
;
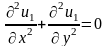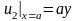
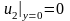
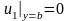
тогда
и учитывая
получаем
используем граничные условия
где
итого
,
тогда
и учитывая
получаем
Используем граничные условия:
,
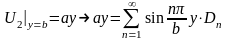где
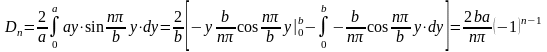
итого получим
Неоднородные задачи со сплошным спектром.
Задача о нагреве полубесконечного стержня
Решение:
;
тогда
Т.к. спектр сплошной, будем искать решение в виде
Тогда
итого
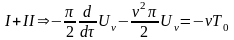
и
тогда частное решение
Подставим граничные условия:
Тогда
Общее решение примет вид
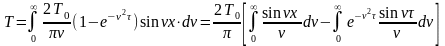
Рассмотрим отдельно:
1)
если
-нечетное,
то
2)
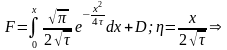
и того
учитывая граничные условия
Тогда
или окончательно
Если зафиксировать определенную температуру:
-
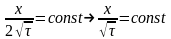
скорость распространения температуры;
т.е. скорость распространения фронта температуры замедляется.
Можно решить задачу проще – метод размерностей. Идея метода:
-
безразмерная и решение так же зависит
от
и
.
пусть
.
Получим дифференциальное уравнение:
;
;
;
Специальные функции
Г-функция (Эйлеров интеграл)
Определение:
Свойства г-функции:
Продифференцируем эту функцию по S:
Проинтегрируем по частям:
при
Рисунок
при
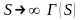стремится к
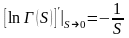
Обобщение Г-функции для отрицательных значений аргумента
Пусть
,
где
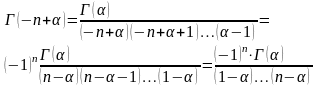
- определение Г-функции для отрицательного аргумента
Рисунок
Рассмотрим
случай, когда
Цилиндрические функции
Это решение уравнения
- уравнение Бесселя
решение:
- функция Бесселя
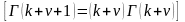
Тождество
удовлетворяется. Функция Бесселя
является решением
Можно
показать, что при
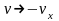уравнение не изменится, поэтому это
тоже является решением. Но будут ли они
линейно независимы? Если
не равно целому числу, то решения от
и от
лнз.
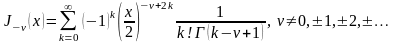
Докажем,
что они лнз, т.е.
- достаточно показать для любого интервала
аргумента.
-
аргумент
- целое отрицательное число, или ноль,
тогда это выражение можно переписать
Сравнивая
это выражение с
,
получаем:
-
л.з.
Вводится функция Неймана как линейная комбинация функции Бесселя для произвольного :
Рассмотрим отдельно:
,
где
Рассмотрим вторую сумму:
Первая сумма:
,
т.е. вся сумма:
Итак:
Т.о.:
,
где
,
- лнз решение функции Бесселя
Частный случай:
-
логарифмическая особенность функции
Неймана в нуле
-
степенная особенность функции Неймана
Итак:
Введём функции Ханкеля I и II рода:
В этом случае:
,
или
и
т.п.
Рекуррентные соотношения для цилиндрических функций - функция Бесселя
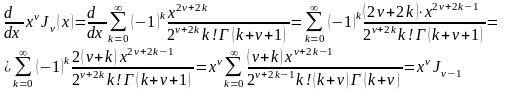
(1)
(2)
Все эти формулы верны для любых цилиндрических функций (Бесселя, Ханкеля и т.п.).
Из (1) и (2):
Сложим и вычтем первое и второе равенство системы:
Пусть
:
(**)
С учётом (**) запишем (*):
-
для задач
Асимметрическое поведение цилиндрических функций при больших значениях аргумента.
Пусть
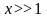
Рассмотрим уравнение Бесселя:
[Если
пренебречь
,
но это очень грубое приближение]
Будем искать решение в виде:
Пренебрегаем последним членом, т.к. :
Решения не зависят от , следовательно, асимптотика одинакова для всех цилиндрических функций.
такие,
что зависят от
следующим образом:
-
асимптотическая функция для функции
Бесселя
-
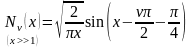асимптотическая функция для функции
Неймана
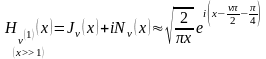
Рисунок