§1.Задача Штурма-Лиувилля
(1)
Уравнение
вида (1) – уравнение Штурма-Лиувилля,
где
– заданные вещественные функции от
аргумента
,
при этом
;
– параметр;
.
– частный
случай, уравнения Штурма-Лиувилля, при
,
.
Граничные условия I рода (типа):
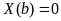
Граничные условия II рода:
Граничные условия III рода:
,
где
– вещественные положительные постоянные.
Всякое нетривиальное решение задачи Штурма-Лиувилля называется собственной функцией; соответствующее значение параметра – собственным значением.
§2. Регулярные и сингулярные задачи
Регулярная
задача – задача, в которой интервал
конечен и его концы не являются особыми
точками (точками, в которых решение
обращается в бесконечность).
Сингулярная задача – задача, в которой хотя бы одно из выше приведенных условий не выполняется.
Примеры сингулярных задач:
,
– регулярный
конец;
– сингулярный конец.
Определение собственных функций и собственных значений
Граничные условия III рода:
совокупность
собственных значений.
Совокупность решений задачи Штурма-Лиувилля называется её спектром.
– совокупность
собственных функций.
1.
,
тогда:
2.
2.1.
;
2.2.
– сингулярная задача.
любое.
§3. Свойства собственных функций и собственных значений
Задача Штурма-Лиувилля:
где
- вещественные;
Начальные условия:
I
рода
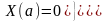
II
рода
III
рода
Совокупность всех решений – спектр
Теорема 1
Собственные значения вещественны
Доказательство:
Пусть - комплексное, тогда для сопряженной задачи Штурма-Лиувилля
(1)
(2)
с начальным условием
,
тогда
Проинтегрируем
по интервалу
:
,
тогда
,
,
т.е.
.
Аналогично
,
тогда останется:
,
учитывая
т.к. мы приняли что - комплексное, то
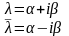
Тогда получим
и
,
а значит - вещественное
Теорема 2
Собственные значения ограничены снизу
Доказательство:
Задача Штурма-Лиувилля
с начальным условием
Проинтегрируем
это выражение:
тогда
,
на принимает ряд значений и имеет минимум и максимум
Пусть
,
тогда
Пример:
,
Теорема 3
Совокупность собственных значений образует дискретный спектр, состоящий из бесконечного множества значений
- бесконечное множество
Разность
между смежными собственными значениями
всегда конечна:
Пример:
,
,
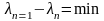если
Теорема 4
Собственные
функции ортогональны на
с весом
:
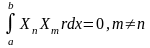
Доказательство:
Каждой
собственной функции присвоим номер и
рассмотрим уравнения для номеров
и
:
с начальными условиями:
(1)
(2)
;
,
как рассматривалось выше
,
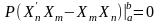тогда остается
Равенство
нулю выполняется, если
(по
условию). Итого получаем:
.
Обозначим норму собственной функции
и получим:
Теорема 5
Если задана любая функция на , то её можно разложить в ряд по собственным функциям задачи Штурма-Лиувилля
и
Доказательство:
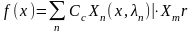
( - фиксированный номер), тогда
.
В
силу ортогональности
при
,тогда
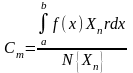
Пример:
ряд
Фурье
,
,
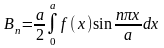
и
,
тогда из теоремы
Рассмотрим
,
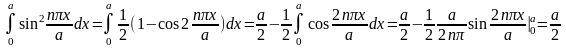тогда
.
Получаем
.
§4.Общая система решения задач методом Фурье.
1.Разделение переменных. Вместо одного уравнения в частных производных, сводим задачу к двум независимым уравнениям с полными производными.
2.Найти собственные функции и собственные значения задачи Штурма-Лиувилля.
3.Поинтегрировать второе (оставшееся) уравнение и построить совокупность частных решений исходной задачи.
4.С помощью теоремы разложения найти коэффициенты разложения и записать окончательный ответ.
Пример: Задача об охлаждающейся пластине по закону Ньютона
Граничные условия:
,
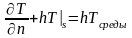и
Начальные условия:
Решение:
Будем
искать решение в виде:
,
тогда получим
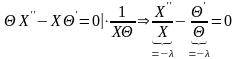
итого получим систему двух уравнений:
Рассмотрим каждое уравнение по отдельности:
1)
с
граничными условиями
и
,
тогда
.
Подставим эти условия:
и
обозначим
и подставим в полученное уравнение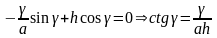
где
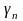- корни уравнения
,
2)
Рассмотрим случай, когда
:
,
тогда получим :
.
Используем начальное условие
используем уже известную формулу для нахождения коэффициентов
.
Вычислим
отдельно знаменатель:
Итого
для коэффициентов
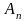получим:
.
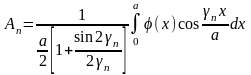Пусть
и вычислим
.
Итого получим окончательный ответ:
Неоднородные задачи МФ.
1)С помощью искусственных приемов
Найти распределение температуры.
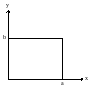
Решение:
Представим
решение в виде:
,
тогда получим 2 уравнения:
и
.
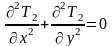А
соответствующие граничные условия
будут 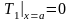для
:
,
,
,
для
:
,
,
,
.
Т.о. мы получили 2 однородные задачи, метод решения которых были рассмотрены ранее.
2)Задача о нагреве шара
Решение:
Будем
искать решение в виде:
.
не зависит от времени, т.к. шар до
нагреваться не может и в конце концов
должна установиться определенная
температура. В итоге получим 2 уравнения:
с граничным условием
и
с граничными условиями
,
.
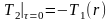Решение подобных задач уже было рассмотрено.
3)Задача о колебании струны
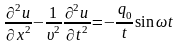
Будем
искать решение в виде:
Для
:
,
тогда
,
сокращая, получим
,
граничные условия:
и
и
.
(подставить)
Для
:
,
граничные условия:
,
,
,
.
Решение подобной задачи рассмотрено ранее.