§6. Метод Фурье (метод разделения переменных)
Примеры, поясняющие идеи метода Фурье.
Пример №1: Задача об охлаждении плоской пластины.
Начальные и граничные условия:
Уравнение теплопроводности:
Произведём замену:
Тогда уравнение теплопроводности примет вид:
Будем искать решение этого уравнения в виде:
Рассмотрим
подробнее первое уравнение системы.
Граничные условия для него такие же,
как и для начальной функции
:
Решение такого уравнения есть:
После подстановки граничных условий получим:
Отсюда имеем трансцендентное уравнение:
Тогда:
Теперь перейдём ко второму уравнению системы. Решением его будет выражение:
Таким образом:
или
Однако это решение не удовлетворяет начальному условию.
Предположим, что
Подставим начальное условие:
Пусть
тогда:
Т.о.:
Примечание:
Нельзя
забывать о возможности равенства
.
Рассмотрим этот случай. Тогда, общее
решение первого уравнения системы будет
равно:
Подставим
граничные условия, получим, что
и
.
Т.е. мы получаем, что при
мы имеем нулевое решение.
Пример №2: Задача об охлаждении шара.
Начальные и граничные условия:
Задача сферически симметрична.
Уравнение теплопроводности в сферических координатах имеет вид:
Решение этого уравнения:
Рассмотрим первое уравнение системы и его решение:
Теперь перейдём ко второму уравнению системы:
(*)
Потребуем, чтобы равенство (*) удовлетворяло начальному условию:
Пусть
тогда:
Итак:
Пример №3: Задача Дирихле для круга.
Будем искать решение в виде:
Потребуем, чтобы
:
Из первого условия:
Из второго:
Т.о.:
Отсюда:
Рассмотрим
случай, когда
:
Граничные условия:
Т.е.
Перейдём ко второму уравнению:
(*)
(*) – уравнение Эйлера
Решение этого уравнения:
Тогда:
Т.о.:
Т.к.
при
,
надо чтобы
,
тогда:
Рассмотрим случай, когда :
Т.к.
при
,
логарифм обращается в бесконечность,
надо чтобы
,
тогда:
Итак:
где
,
.
Потребуем, чтобы это выражение удовлетворяло условию :
т.о.,
ряд Фурье.
Преобразование решения Пуассона:
Проведём несколько замен:
Учитывая,
что
,
получим:
Из теории рядом следует, что:
.
Тогда:
Итак:
(**)
(**) – интеграл Пуассона – решение задачи Дирихле для круга.
Пример №4: Задача об охлаждении полу бесконечного стержня.
,
Будем искать решение этого уравнения в виде:
Решение первое уравнения имеет вид:
Граничное условие:
Отсюда:
Потребуем, чтобы это решение было ограничено на бесконечности. Для этого синус должен оставаться ограниченным, т.е. его аргумент должен быть вещественным. Это значит, что .
Пусть
,
где
.
Тогда:
Рассмотрим случай, когда :
Теперь разберём второе уравнение. Решением его будет выражение вида:
(*)
(*) – частное решение, т.к. оно не удовлетворяет граничным условиям.
Потребуем, чтобы это уравнение граничным условиям удовлетворяло:
Преобразуем
решение, т.е. перейдём от
к
:
Учтём, что
тогда:
Рассмотрим интеграл вида:
Произведём дифференцирование по параметру:
Т.о.:
Тогда:
Т.о.:
Пример №5: Задача Дирихле для полуплоскости.
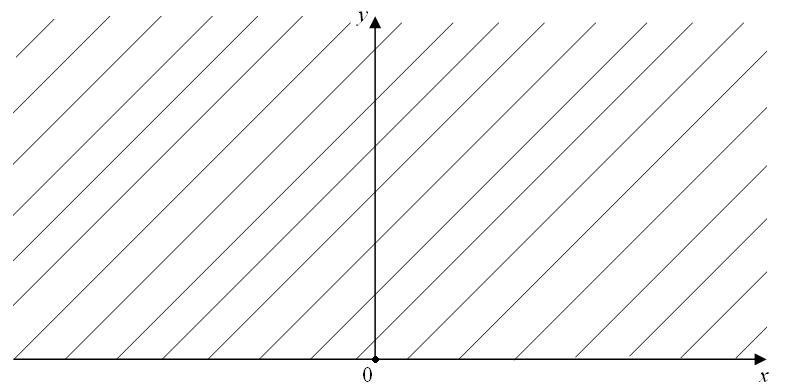
Будем искать решение в виде:
Решение первого уравнения имеет вид:
Пусть
где
,тогда:
,
т.к. при
,
первое слагаемое будет стремиться к
бесконечности, поэтому:
Перейдём к решению второго уравнения:
,
т.к. при
,
первое слагаемое также будет стремиться
к бесконечности, поэтому:
Тогда:
Преобразование решения:
Рассмотрим интеграл вида:
Итак:
Применим этот результат к нашему решению:
А этот результат используем для следующей задачи: найти стационарное распределение температуры в полуплоскости, если:
Произведём замену:
Тогда:
Пример №6: Задача Дирихле для сектора.
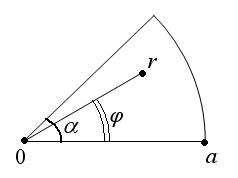
Будем искать решение в виде:
Найдём решение первого уравнения:
Решение этого уравнения имеет вид:
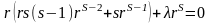
Т.о.:
Учитывая,
что
,
перепишем это решение в виде:
А
так же учтём соотношение вида
тогда:
не
может быть мнимой величиной, т.к. в
интеграле Фурье должны присутствовать
только вещественные аргументы.
где
т.к.
,
поэтому:
Теперь перейдём ко второму уравнению системы:
Тогда:
(*)
(*) – частное решение.
Просуммируем все решения и потребуем выполнения условий и :
Т.о.:
Т.е.:
Это выражение не является интегралом Фурье, поэтому введём новую переменную
(**)
(**) – интеграл Фурье.
Тогда:
По
этой формуле так же можно вычислить
коэффициенты
и
.
Итак:
,
где:
Теория собственных функций