5. Образ пути при преобразовании расписания

В матрице A(𝜋) = [A_p(1), A_p(2), ..., A_p(n)] времен выполнения работ расписания рассмотрим сегмент образованный при пересечении пути S_u с r-м столбцом A_p(r), r = :

(10)

Введем понятие образа пути.

Пусть π₁(p₁) - расписание, полученное в результате применения оператора к расписанию π(p): π₁(p₁) = . Пусть S_u - некото­рый путь в матрице A(π). Разобьем этот путь на три сегмента:

так что Рассмотрим теперь матрицу выделим в ней путь сегменты которого в зависимости от соотношения между индексами преобразования k и l определятся следующим образом:

1. при k=l

2. при k<l

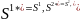
3. при k>l

Пусть k≠l. В соответствии с определением оператора преобразования

Поэтому путь 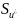всегда существует. Из определения оператора преобразования следует также, что между множествами элементов , расположенных на путях 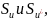может быть установлено соответствие:

Заметим что

Путь в матрице будем называть образом пути в матрице

Лемма 1. Пусть S_u - произвольный критический путь в матри­це - образ этого пути в матрице Тогда

Доказательство. Утверждение справедливо, поскольку об­раз S_u* является путем в матрице

Лемма доказана.

Прокомментируем нестрогое неравенство в лемме 1. Путь S_u* в матрице может оказаться критическим (и тогда неравенст­во обращается в равенство), но вовсе не обязательно является тако­вым (в этом случае неравенство становится строгим).

Аппарат образов путей очень удобен при проведении оптимиза­ционных исследований и, в частности, при анализе эффективности преобразований. Последнее замечание становится очевидным, если учесть возможность сопоставления длины С(π) исходного расписа­ния π и оценки (снизу) длины C(π₁) его расписания-потомка π₁. В качестве нижней оценки величины C(π₁) при этом можно исполь­зовать сумму

6.Оценка эффективности преобразований

Эффективные преобразования уменьшают значение критерия качества расписания («улучшают» расписание) поэтому одним из подходов к решению задачи поиска расписания минимальной длины является определение множества эффективных преобразований

Для пути и индексов определим:

Отметим:

Справедливость соотношения (12) вытекает непосредственно из определения величины в соотношении (11)

Лемма 2. Справедливы неравенства

Из леммы 2 следует, что величину при каждом и каждом можно рассматривать как прогноз (оценку) эффективности преобразования .

7.Выявление неэффективных преобразований

Лемма 2 допускает интерпретацию: если в матрице времен выполнения работ расписания π существует критический путь S_u 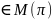, такой, что для пары индексов (k, l) выполняется неравен­ство , то преобразование неэффективно. Приведем еще одно утверждение, которое наряду с этим признаком указывает на неэффективность преобразования.

Утверждение 1.

Изменения очередности выполнения работ внутри группы с номе­рами с v-го по w-й не приводят к менее длинному, чем исходное, расписанию.

Продемонстрируем использование системы оценок и ут­верждения 1 для выявления неэффективных преобразований.

Пример 4. Расписание

	1	2	3	4	5	6
A(π) =	1	9	1	1	1	1
	1	9	1	1	1	1
	1	2	3	4	5	6

В матрице имеется единственный критический путь S₁.

Проведем анализ эффективности преобразований для всех . Прежде всего, отметим, что утверждение 1 остается в силе при v = 1 (если r = 1) и w = n (если r = m); в этих случаях вместо сегмента следует иметь в виду соответственно.

1. Из условия следует, что для всех возмож­ных пар

2. Соответствующие преобразования неэффективны.

3. для всех возможных пар Соответствующие преобразования неэффективны.

4. 

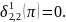
5. Соответствующие преобразования могут оказаться эффективными.