МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

ВОЛЖСКИЙ ГУМАНИТАРНЫЙ ИНСТИТУТ

(ФИЛИАЛ)

ФЕДЕРАЛЬНОГО ГОСУДАРСТВЕННОГО БЮДЖЕТНОГО ОБРАЗОВАТЕЛЬНОГО УЧРЕЖДЕНИЯ

ВЫСШЕГО ПРОФИСИОНАЛЬНОГО ОБРАЗОВАНИЯ «ВОЛГОГРАДСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ»

факультет естественных и гуманитарных наук

кафедра прикладной математики и информатики

КУРСОВАЯ РАБОТА

ОПТИМИЗАЦИЯ РАБОТЫ СИСТЕМ ПОСЛЕДОВАТЕЛЬНОГО ТИПА

Выполнил: студент группы ПМФ-091

Симонов Е.А.__________

(подпись)

Научный руководитель

д.т.н., профессор

Мирецкий И.Ю.__________

(подпись)

Волжский 2012 г.

Содержание:

Введение………………………………………………………………………..3

1. Постановка задачи………………………………………………………………..…....4

2. Математическая модель…………………………………………………………………….5

3. Оператор преобразования 𝛀_k,l………………………………………………………………………...8

4. Субоптимальные расписания……………………………………………............................13

5. Образ пути при преобразовании расписания………………………………………………………………18

6. Оценка эффективности преобразований…………………………………………………………20

7. Выявление неэффективных преобразований……………………………............................................21

8. Условия 1-оптимальности расписания………………………………………………………………23

9. 1-оптимальные алгоритмы……………………………………………………………….23

Список используемой литературы…………………………………………...26

Введение

В прошлых курсовых работах мной были рассмотрены задачи теории расписаний для 1 машины, 2 машин, а также некоторые случаи задачи для 3 машин. В общем же случае алгоритмы решающие задачу точно имеют экспоненциальную сложность. А в случае достаточно большого количества машин и работ, как обычно и бывает на практике, их реализация требует огромных временных затрат. Поэтому практическую ценность имеют, в основном, алгоритмы полиномиальной сложности. Для случаев 1 и 2 машин, они давали точные решения, но в других случаях – это бывает крайне редко. Рассмотрение алгоритмов, которые будут давать приближенно оптимальные решения и имеющие полиномиальную сложность, и будет являться темой данной курсовой работы. Конкретно будут рассмотрены методы нахождения локально-оптимальных решений. (Но существуют и другие алгоритмы приближенного решения полиномиальной сложности)

1.Постановка задачи

Система обработки состоит из m последовательно работающих машин M₁, … , M_m. На машинах требуется выполнить n работ t₁ , …, t_n. Для этой системы известно что:

1. Все машины системы абсолютно надежны.

2. К моменту начала функционирования конвейерной системы все работы доступны.

3. Работа t_j, j= 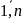, состоит из m операций O_1j, … , O_mj, причем каждая операция O_ij выполняется соответствующей машиной M_i , i= . Длительности операций O_ij равны a_ij.

4. Маршрут прохождения по машинам одинаков для всех работ M₁, … , M_m

5. Очередность выполнения работ на всех машинах одна и та же.

6. Каждая машина начинает выполнение работы сразу после ее поступления (если машина свободна) либо после завершения преды­дущей работы (если она занята).

7. Каждая машина одновременно может выполнять не более од­ной работы.

8. Начавшаяся операция не прерывается до полного ее завершения.

9. Длительности операций не зависят от последовательности, в которой они выполняются.

10. Времена транспортировки обрабатываемых изделий и пере­наладки машин включены в длительности операций.

Требуется определить оптимальную последовательность обработ­ки (расписание), для которой общее время выполнения всех работ на всех машинах (время прохождения, длина расписания) минимально.

В соответствии с общепринятой классификацией поставленная задача называется permutation flow shop problem (конвейерной зада­чей) и имеет символическое представление Fm | perm | C_max. Задача относится к числу NP-трудных.