
- •Содержание:
- •Введение
- •1.Постановка задачи
- •2.Математическая модель
- •3.Оператор преобразования 𝛀k,l
- •4.Субоптимальные расписания
- •5. Образ пути при преобразовании расписания
- •6.Оценка эффективности преобразований
- •7.Выявление неэффективных преобразований
- •8.Условия 1-оптимальности расписания
- •Список используемой литературы:
3.Оператор преобразования 𝛀k,l
Пусть π(p) - произвольное расписание с матрицей времен выполнения A(π) = [Ap(1), Ap(2), ..., Ap(n)]. Зададим над π оператор преобразования 𝛀k,l, k ∈ {1, 2, ..., n}, t ∈ {1, 2, ..., n}. Оператор изменяет очередность выполнения работ машинами системы (задает новую перестановку номеров работ; в частности, работа, которой соответствует столбец Ap(k), перемещается в упорядочении на l-ю позицию). Он выполняет преобразование расписания π(p) с матрицей времен выполнения
A(π) = [Ap(1), Ap(2), ..., Ap(n)]
в расписание π1 = 𝛀k,l (π), матрица A(π1) времен выполнения которого строится по следующим правилам:
при k > l
A(π1) = [Ap(1), Ap(2), ..., Ap(k-1), Ap(k+1), … , Ap(l), Ap(k), Ap(l+1), … , Ap(n)]
при k < l
A(π1) = [Ap(1), Ap(2), ..., Ap(l-1), Ap(k), Ap(l), … , , Ap(k-1), Ap(k+1), … , Ap(n)]
при k = l (оператор переводит расписание само в себя)
A(π1)≡A(π).
Оператор 𝛀k,l (π) при k = l будем называть пустым, при k ≠ l - непустым.
Будем говорить, что оператор 𝛀k,l (π) переносит работу tp(k) и осуществляет сдвиг влево при k < l на 1 позицию работ tp(k+1), ..., tp(l) (сдвиг вправо при k > l - работ tp(l), ..., tp(k-1)). При этом отношения предшествования “≺ ” для всех работ, за исключением пар, содержащих работу tp(k), не изменяются.
Заметим, что для каждого преобразования существует обратное преобразование. Так, если π1(p1) = 𝛀k,l (π (p)), то π(p) = 𝛀l,p(k) (π1 (p1)). Поэтому 𝛀l,p(k) (𝛀k,l (π (p)))= π(p)
Конструкцию

будем
называть композицией
операторов преобразования (композицией
преобразований, или просто композицией).
Композиции есть последовательность
преобразований

где


………………………………………………………………………

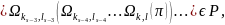

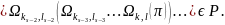
Расписание

однозначно
определяется расписанием π
и набором индексов k,
l и
 ,где
j=
,где
j=
Транспозиция двух работ в расписании описывается композицией из двух операторов преобразования. Так, расписание


k
< l
(равно, как и π1
= ,
k
> l)
отличается от расписания π
транспозицией работ
,
k
> l)
отличается от расписания π
транспозицией работ
 и
и
 .
.
Определение
4. Расписание π1
=
 называется непосредственным
потомком (непосредственным преемником)
расписания π
при преобразовании
.
называется непосредственным
потомком (непосредственным преемником)
расписания π
при преобразовании
.
Определение 5. Расписание π1, полученное в результате композиции преобразований расписания π, называется потомком (преемником) последнего.
В только что приведенном определении композиции расписания π1, π2, ..., πs - потомки расписания π, расписания π2, π3, ..., πs - потомки расписания и т. д.
Определение 6. Расписание π называется исходным по отношению ко всем своим потомкам.
Определение
7. Число непустых операторов преобразования
 ,
входящих в композицию, называется длиной
композиции.
,
входящих в композицию, называется длиной
композиции.
Длина композиции, состоящей из одного оператора, есть либо 0 (в случае пустого оператора), либо 1 (в случае непустого оператора).
Длина транспозиции равна 2.
Теорема 1. Пусть π1(p1) ∈ P и π2(p2) ∈ P - два произвольных расписания для одной системы заданий из n работ. Тогда одно расписание может быть получено из другого s-кратным (s ≤ n - 1) применением оператора .
Доказательство.
Пусть расписание π2(p2)
есть потомок расписания π1(p1)
(исходного). Зафиксируем последнюю
работу
 в
расписании π2(p2).
в
расписании π2(p2).
Определим значение индекса r из условия

(работа
 занимает в расписании
занимает в расписании
 r-ю
позицию). Очевидно, что получить расписание
r-ю
позицию). Очевидно, что получить расписание
 (p2)
из π1(p1)
можно, последовательно выполняя операции
переноса работ
(p2)
из π1(p1)
можно, последовательно выполняя операции
переноса работ
 j
∈{1,
2, ..., n}\{r}
(не подвергая переносу работу
).
Очевидно также, что минимальное число
подобных операций переноса не превосходит
n
-
1.
j
∈{1,
2, ..., n}\{r}
(не подвергая переносу работу
).
Очевидно также, что минимальное число
подобных операций переноса не превосходит
n
-
1.
Неулучшаемость верхней оценки (s = n - 1) продемонстрируем следующим примером: n = 3, (p1), π2(p2) ∈ P, p1 = (1, 2, 3), p2 = (3, 2, 1). Очевидно, s = 2.
Теорема доказана.
Далее
при сопоставлении расписаний будем
полагать, что они соответствуют одной
системе заданий.
Пример 2. Выполним преобразования. Пусть на обработку в конвейерную систему из четырех машин поступают шесть заданий- работ t1, t2, ., t6. Длительности операций определены векторами
A1 = [1,1,1,1]T, A2 = [2,9,9,2]T, A3 = [3,1,1,3]T,
A4 = [4,1,1,4]T, A5 = [5,1,1,5]T, A6 = [6,1,1,6]T
Пусть расписание

задано
матрицей


рассмотрим
преобразование
 Построим
матрицу времени выполнения
Построим
матрицу времени выполнения
 расписания
расписания
 и
вычислим длину этого расписания.
и
вычислим длину этого расписания.

Вычислим
длину расписаний: имеем

Схема
преобразований
 такова:
такова:















Пример 3. Схема выполнения композиции преобразований 𝛀3,5 (𝛀4,2 (π))расписания π(p) = (t1,t2, t3, t4, t5, t6):
t1 
t2 
t3 
t4 

t6

Рассмотрим два расписания π и π1 = (π). Определим меру эффективности Δ преобразования относительно критерия Cmax:
Δk,l(π) = max{C(π) - С(π 1, 0}. (9)
Определение 8. Преобразование (π) называется эффективным относительно критерия Cmax, если Δk,l(π) > 0. В противном случае преобразование называется неэффективным относительно критерия Cmax.
Аналогичным образом определим эффективность композиции преобразований.
Множество эффективных преобразований расписания π обозначим Ω+
В примере 2 преобразование Ω5,2(π) является неэффективным, Δ5,2(π) =0.
