10. Уравнение с разделяющимися переменными

Дифференциальное уравнение

(3.1)

называется уравнением с разделяющимися переменными.

Умножая обе части уравнения на , получаем уравнение

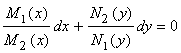(3.2)

В уравнении (3.2) коэффициент при dx зависит только от x, а коэффициент при dy зависит только от y. Значит, в уравнении (3.2) переменные разделены. Интегрируя, получаем:

+

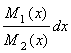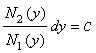
Пример.3.1 . Найти частное решение уравнения,  удовлетворяющее начальным данным:  при  x=1,  y=1. 

Преобразуем уравнение ; . Умножая оби части уравнения на , получаем уравнение с разделенными переменными . Интегрируем:

+ ; + ;

; .

По начальным данным находим c (в последнее уравнение подставляем  x=1,  y=1):

1+1+0=c, c=2; - искомое частное решение.

Пример. 3.2

Заменяем  на : , переменные

разделились. Интегрируем: = , ,

- общее решение.

Практически решение  большинства типов дифференциальных уравнений сводится к решению  уравнений с разделяющимися переменными, методы сведения разнообразны и зависят от типа уравнения.

Например, в уравнении

(3.5)

 

где a и b константы можно разделить переменные, сделав замену z=ax+by.

Так как , то , переменные разделились,

интегрируем                                              = .

11. Однородное дифференциальное уравнение

Перейти к: навигация, поиск

Существует два понятия однородности дифференциальных уравнений.

1

Обыкновенное уравнение первого порядка называется однородным относительно x и y, если функция является однородной степени 0:

.

Однородную функцию можно представить как функцию от :

.

Используем подстановку , а затем воспользуемся правилом произведения : . Тогда, дифференциальное уравнение сводится к уравнению с разделяющимися переменными:

.

2

Дифференциальное уравнение является однородным, если оно не содержит свободного члена — слагаемого, не зависящего от неизвестной функции. Так, можно говорить, что уравнение  — однородно, если .

В случае, если , говорят о неоднородном дифференциальном уравнении.

Именно для решения линейных однородных диф. уравнений была построена целая теория, чему способствовало выполнение у них принципа суперпозиции.

12.Линейные дифференциальные уравнения

с постоянными коэффициентами

Уравнение

(9.1) называется линейным дифференциальным уравнением n-го порядка с постоянными коэффициентами; - постоянные вещественные числа. Если функция ) не равна тождественно нулю, то иногда говорят, что уравнение с правой частью.

Уравнение

(9.2) называется линейным однородным дифференциальным уравнением n-го порядка с постоянными коэффициентами; - постоянные вещественные числа. Т. к. функция ) равна тождественно нулю, то иногда говорят, что уравнение без правой части.

Уравнение (9.3)

называется характеристическим уравнением, а его корни – характеристическими числами уравнения (9.2).

Система функций называется линейно независимой в интервале , если тождество ( - постоянные числа)

может выполняться только когда все . Если к тому же каждая из функций является частным решением однородного уравнения (9.2), то система решений одно-родного уравнения называется фундаментальной системой решений.

Если фундаментальная система решений найдена, то функция

дает общее решение однородного уравнения (9.2), ( все - константы ).