8.Несобственные интегралы II рода

Пусть определена на , терпит бесконечный разрыв в точке x=a и 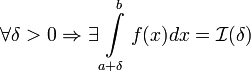. Тогда:

1. Если 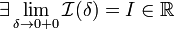, то используется обозначение 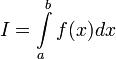и интеграл называется несобственным интегралом Римана второго рода. В этом случае интеграл называется сходящимся.

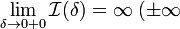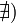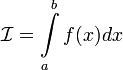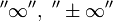2. Если или , то обозначение сохраняется, а называется расходящимся к , или просто расходящимся.

Пусть определена на , терпит бесконечный разрыв при x=b и 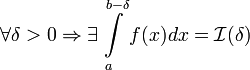. Тогда:

1. Если , то используется обозначение и интеграл называется несобственным интегралом Римана второго рода. В этом случае интеграл называется сходящимся.

2. Если или , то обозначение сохраняется, а называется расходящимся к , или просто расходящимся.

Если функция терпит разрыв во внутренней точке отрезка , то несобственный интеграл второго рода определяется формулой:

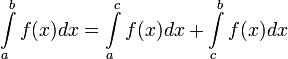
Геометрический смысл несобственных интегралов II рода

Несобственный интеграл выражает площадь бесконечно высокой криволинейной трапеции

Пример

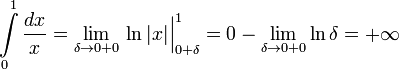
9. дифференциальные уравнения.основные понятия

Определение. Функциональное уравнение , связывающее между собой независимую переменную , неизвестную функцию  и ее производные , … , называется дифференциальным уравнением.

Порядок старшей производной неизвестной функции определяет порядок дифференциального уравнения.

Так, уравнение является уравнением первого порядка, уравнение - уравнением второго порядка.

Рассмотрим дифференциальное уравнение первого порядка .

Определение. Всякая функция , которая, будучи подставлена в уравнение вместе со своей производной , обращает его в тождество относительно , называется решением этого уравнения.

Определение. Общим решением дифференциального уравнения первого порядка называется такая функция , которая при любом значении  является решением этого дифференциального уравнения.

Общее решение дифференциального уравнения представляет собой множество функций, удовлетворяющих уравнению.

Например, решим уравнение . Легко видеть, что  (вспомните, что производная функции  равна ). Таким образом, давая постоянной  различные значения, мы получим множество прямых, параллельных прямой .

Иногда из всех функций  требуется выделить такую, что для фиксированных и .Условие называют начальным условием. Если требуется найти такое решение уравнения  или , которое удовлетворяет начальному условию , то говорят, что требуется решить задачу Коши.

Записывают задачу Коши так:

 

 

,                            ,

                                  при .

Примеры ОДУ. а) Известную из математического анализа задачу отыскания всех первообразных данной функции f можно записать в виде уравнения

y′ = f(x),

(1)

где f — данная непрерывная функция, y = y(x) — неизвестная функция, y′ = dy/dx; оно представляет собой простейший пример ОДУ. Как доказывается в интегральном исчислении, если f непрерывна на промежутке J, то уравнение (1) имеет на нем бесконечное семейство решений, которое задается формулой

y = F(x) + C;

(2)

здесь F — какая-нибудь фиксированная первообразная функции f, а параметр C пробегает все вещественные значения.

б) Замечательным свойством функции y = e^x является то, что она совпадает со своей производной; это свойство записывается в виде ОДУ

y′ = y,

(3)

решениями которого, наряду с e^x, будут все функции семейства

y = Cex.

(4)

в) С учетом механического смысла второй производной (ускорение) уравнение прямолинейного равноускоренного движения записывается в форме

x.. = a.

(5)

Точками здесь (и часто в дальнейшем) обозначаются производные по времени. Последовательное интегрирование (5) в пределах от 0 до t дает:

x. = at + v0    (v0 = x.(0)),

(6)

x =  at2 2   + v0t + x0    (x0 = x(0)).

(7)

г) Если в уравнении окружности

x2 + y2 = R2

(8)

переменные x и y считать гладкими функциями параметра s: x = x(s), y = y(s) — и продифференцировать (8) по s, то получится дифференциальное уравнение семейства всех окружностей с центром в начале координат:

x dx ds  + y dy ds  = 0.

(9)

д) Одним из решений уравнения (9) является пара функций

x = sin s, y = cos s.

(10)

Очевидно, эта пара удовлетворяет также следующей системе дифференциальных уравнений:

x′ = y, y′ = –x.

(11)

1.1.2. Общий вид ОДУ. В общей ситуации мы, как правило, будем обозначать значения неизвестной функции буквой x, независимой переменной — t (и интерпретировать ее как время), производных от x по t — x′, x′′, ..., x^(m). Мы будем также использовать сокращенное обозначение J^(m)x = (x, x′, ..., x^(m)) — этот вектор называют струей, или джетом m-го порядка функции x в точке t. В дифференциальные уравнения может входить также набор C = (C₁, C₂, ..., C_p) произвольных постоянных (параметров). Тогда произвольное ОДУ с одной неизвестной функцией может быть, по определению, записано в виде

F(t, J(m)x, C) = 0.

(12)

Когда нужно подчеркнуть наличие в уравнении параметра C мы будем говорить о семействе ОДУ, зависящих от параметра C = (C₁, C₂, ..., C_p).

Наряду с такими уравнениями мы будем рассматривать системы ОДУ с несколькими неизвестными:

F1(t, J(m)x, C) = 0, F2(t, J(m)x, C) = 0, . . . Fk(t, J(m)x, C) = 0;

(13)

в нем теперь

x = (x1, x2, ..., xn), m = (m1, m2, ..., mn), J(m)x = ( J(m1)x1, J(m2)x2, ..., J(mn)xn), J(mi)xi = (xi, x′i,..., xi(m1)).