
- •Раздел 7. Калориметрия
- •22.2. Классификация калориметров
- •22.3. Теплоемкость
- •22.3.1. Теплоемкость кристаллов. Модели Дебая и Эйнштейна.
- •22.4. Классификация методов измерений теплоемкости
- •23. Адиабатическая калориметрия
- •23.1. Устройство калориметрической установки.
- •23.2. Измерение и регулирование термодинамических параметров.
- •23.3. Погрешность измерений теплоемкости
- •23.4. Калориметрический сосуд
- •23.5. Измерения в режиме непрерывного нагрева
- •23.6. Преимущества и недостатки адиабатической калориметрии
- •24. Термический анализ
- •24.1. Что такое термический анализ?
- •24.1. Термогравиметрический анализ
- •24.2. Дифференциальный термический анализ (дта)
- •24.3. Дифференциальная сканирующая калориметрия
- •24.4. Дифференциальные сканирующие микрокалориметры дсм-2м, дсм-10м
- •24.5. Дск калориметры фирмы “Netzsch”
22.3. Теплоемкость
Теплоемкость - физическая величина, характеризующая количество теплоты, которое вещество должно получить от окружающей среды при определенных условиях, чтобы его температура поднялась на один градус.
В
зависимости от условий теплообмена
различают теплоемкость при постоянном
объеме (![]() )
и теплоемкость при постоянном давлении
(
)
и теплоемкость при постоянном давлении
(![]() ).
Теплоемкость веществ чаще всего
выражается в виде удельной величины,
отнесенной к единице массы - [Дж/(кг К)],
к единице количества вещества - [Дж/(моль
К)] или к единице объема - [Дж/(м3
K].
).
Теплоемкость веществ чаще всего
выражается в виде удельной величины,
отнесенной к единице массы - [Дж/(кг К)],
к единице количества вещества - [Дж/(моль
К)] или к единице объема - [Дж/(м3
K].
Необходимость знания теплоемкости веществ определяется в первую очередь двумя важнейшими факторами: во-первых, из научной значимости, являясь ценнейшим источником информации при исследованиях в термодинамике, в физике твердого тела при исследованиях структуры веществ, сил взаимодействия, фазовых переходов, критических явлений и т.д.; во-вторых, из практической значимости, вытекающей из необходимости знаний этой физической величины наряду с другими во многих инженерных расчетах тепловых процессов и аппаратов современных технологий. При этом точность таких знаний во многом определяет рациональность выбранных конструкций, размеров, режимов работы и, в конечном счете, эффективность разработки в целом.
Впервые понятие теплоемкость было введено Дж. Блэком в 1760 г. и исторически развивалось неразрывно с понятиями теплота и калория.
Так
как по определению
![]() ,
то из основного (1-го) начала термодинамики
в зависимости от условий протекания
процесса следует
,
то из основного (1-го) начала термодинамики
в зависимости от условий протекания
процесса следует
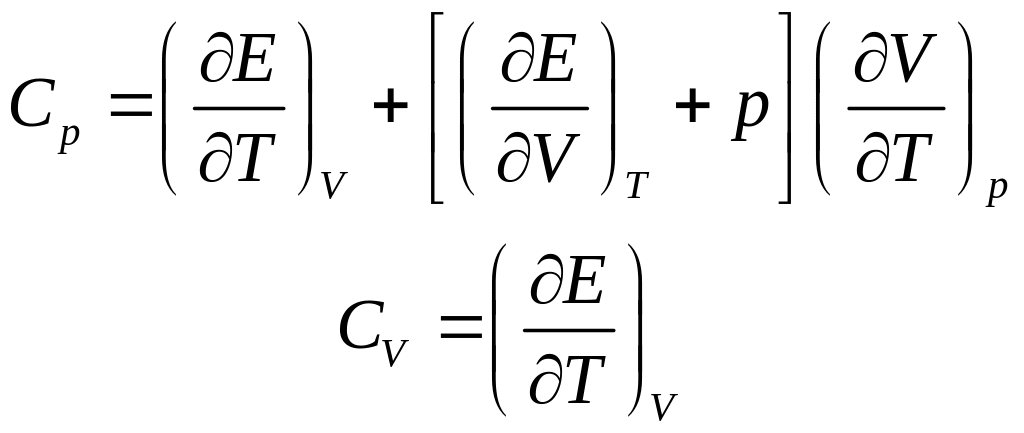 (22.2)
(22.2)
Разница
между изобарной и изохорной теплоемкостями
определяет количество теплоты, пошедшее
на работу
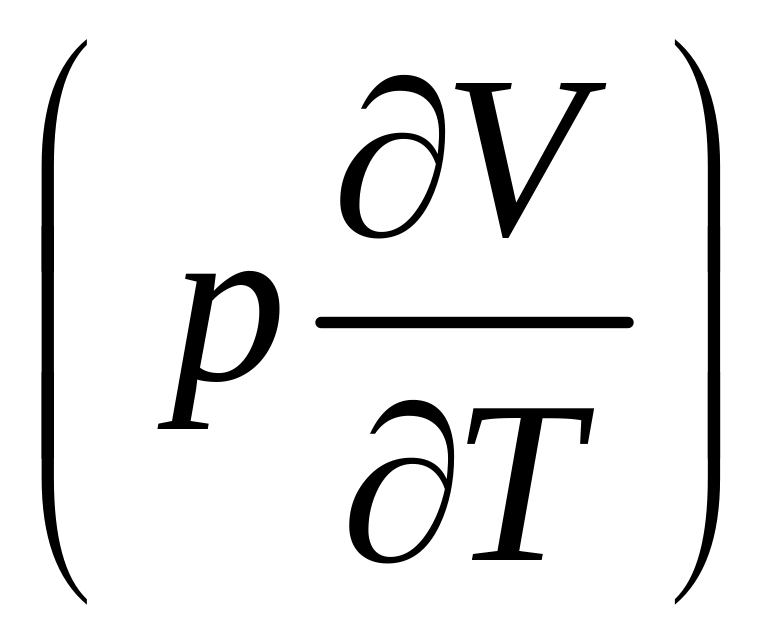 и на изменение внутренней энергии
системы
и на изменение внутренней энергии
системы
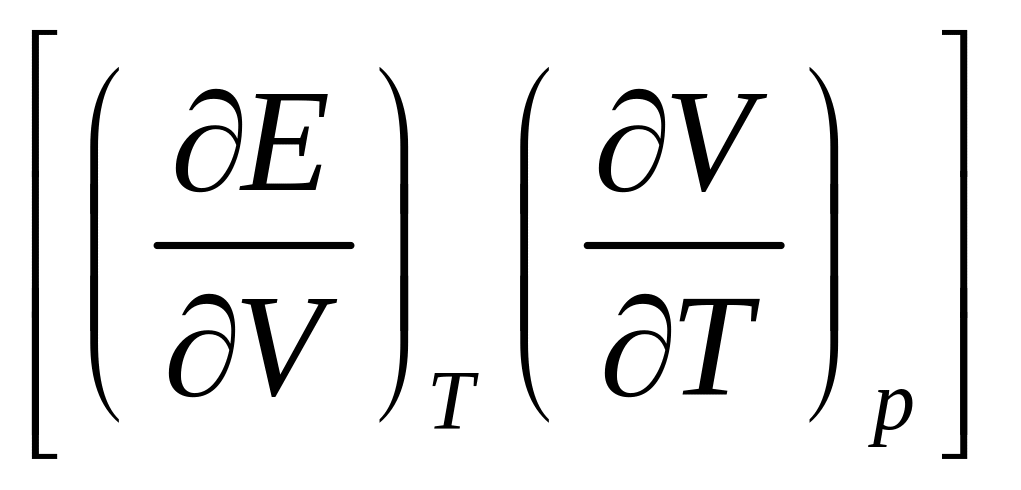 ,
связанное с изменением объема. Для
жидких и твердых тел эта разница обычно
невелика, поэтому в технических расчетах
ею часто пренебрегают, пользуясь без
особых оговорок экспериментальными
значениями изобарной теплоемкости.
Определенная таким образом удельная
теплоемкость в единицах энергии, (в
которых мы определяем и количество
теплоты), на градус температуры в
избранной шкале. Следовательно, величина
теплоемкости зависит от температурной
шкалы.
,
связанное с изменением объема. Для
жидких и твердых тел эта разница обычно
невелика, поэтому в технических расчетах
ею часто пренебрегают, пользуясь без
особых оговорок экспериментальными
значениями изобарной теплоемкости.
Определенная таким образом удельная
теплоемкость в единицах энергии, (в
которых мы определяем и количество
теплоты), на градус температуры в
избранной шкале. Следовательно, величина
теплоемкости зависит от температурной
шкалы.
При
измерении теплоемкости твердых веществ
и жидкостей, как правило, измеряют
.
Эксперименты по прямому измерению
уникальны. Связано это с тепловым
расширением исследуемого образца при
его нагреве в процессе измерений. Из-за
очень малой сжимаемости конденсированных
сред практически невозможно изготовить
измерительную ячейку, которая бы не
деформировалась под воздействием
возникающих при нагреве образца сил,
т. е. обеспечить выполнение условия
![]() = const не удается. То, что коэффициенты
теплового расширения твердых тел и
жидкостей малы и при нагреве на несколько
градусов объем образца увеличивается
незначительно, не должно вводить в
заблуждение. Здесь важна качественная
сторона: какой из внешних параметров
(
или
)
поддерживается постоянным. При высоких
температурах
может отличаться от
весьма значительно.
= const не удается. То, что коэффициенты
теплового расширения твердых тел и
жидкостей малы и при нагреве на несколько
градусов объем образца увеличивается
незначительно, не должно вводить в
заблуждение. Здесь важна качественная
сторона: какой из внешних параметров
(
или
)
поддерживается постоянным. При высоких
температурах
может отличаться от
весьма значительно.
Строгое термодинамическое соотношение, связывающее и имеет вид
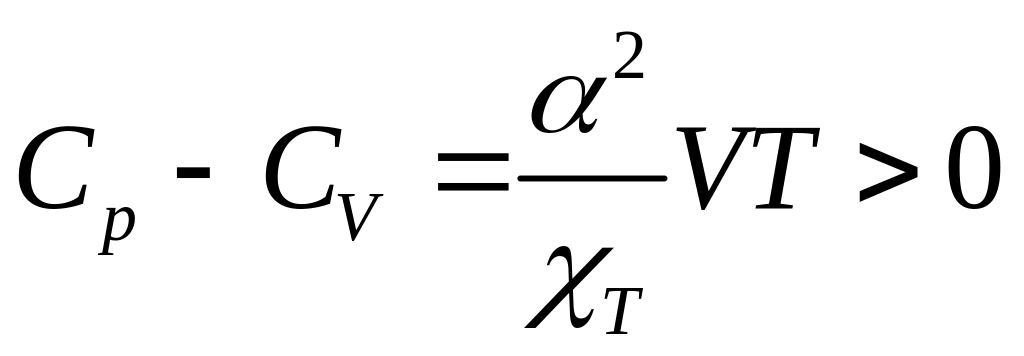 (22.3)
(22.3)
где
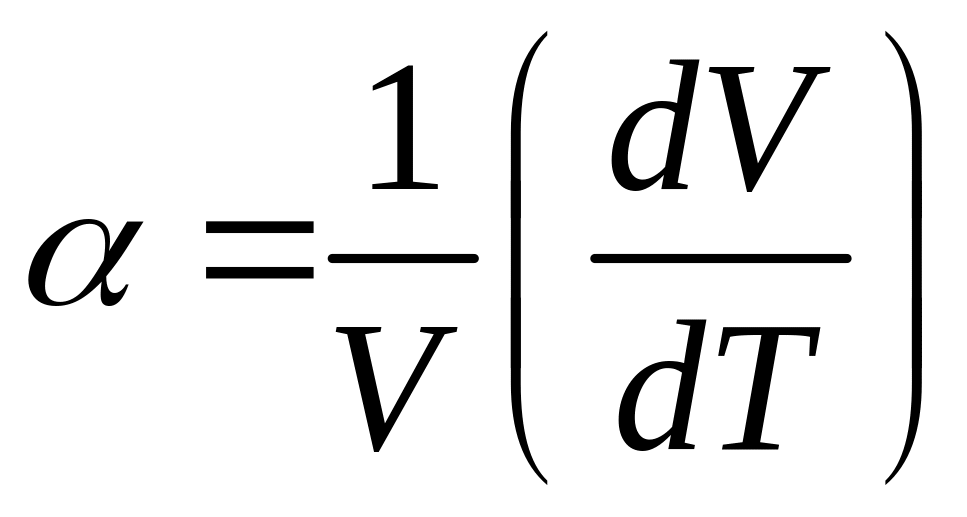 (22.4)
(22.4)
коэффициент теплового расширения,
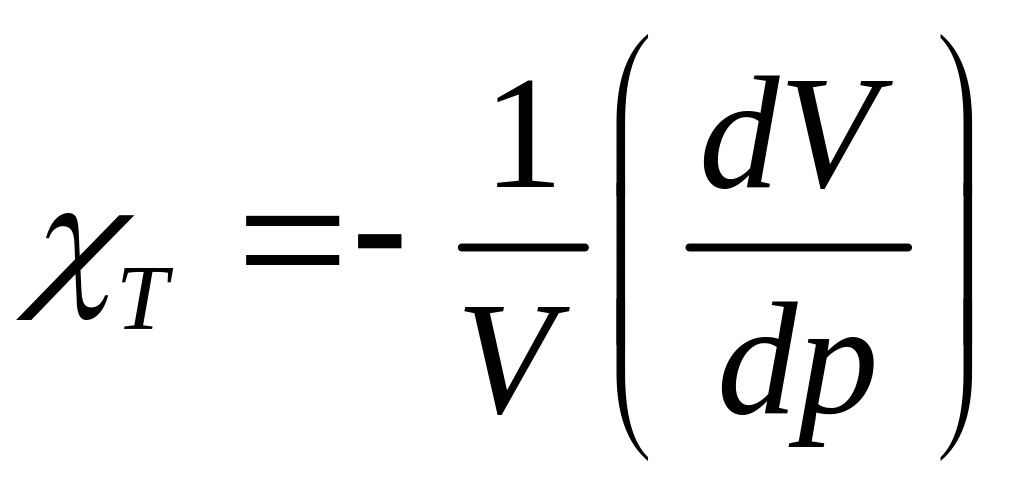 (22.5)
(22.5)
изотермическая сжимаемость.
Для 1 моля идеального газа, как вы помните,
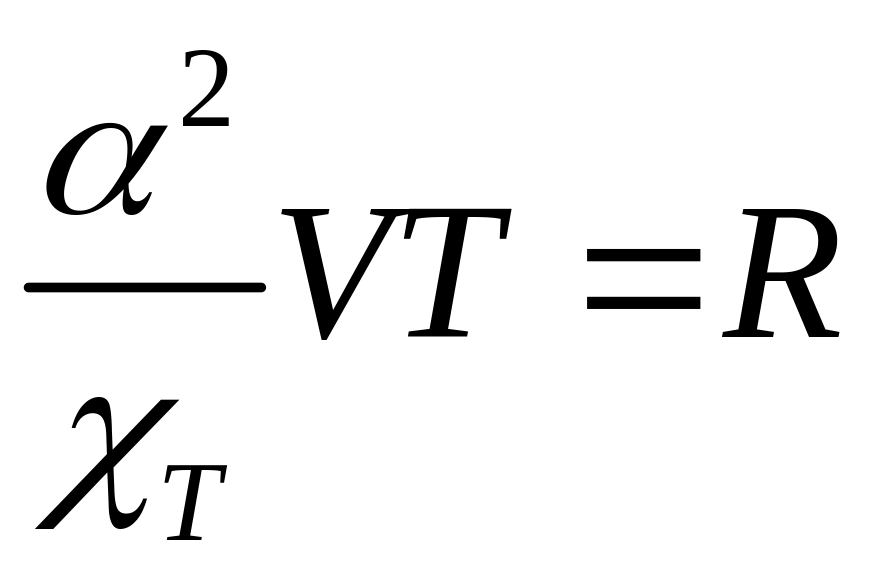 (22.6)
(22.6)
![]() =
8.314 Дж/моль К.
=
8.314 Дж/моль К.
Основной
вклад в теплоемкость твердых тел дают
тепловые колебания кристаллической
решетки. В гармоническом приближении
(теория Дебая) при температурах выше
некоторой характеристической температуры
![]() (температура Дебая),
не зависит от температуры:
(температура Дебая),
не зависит от температуры:
![]() = 3R
= const. Температура Дебая является
индивидуальной характеристикой вещества.
Значения
некоторых веществ приведены в таблице
22.1.
= 3R
= const. Температура Дебая является
индивидуальной характеристикой вещества.
Значения
некоторых веществ приведены в таблице
22.1.
При
температуре близкой к
(для большинства веществ это область
комнатных или несколько больших
температур, (см. таблицу )
![]() что
видно из таблицы. (Таким образом, вы
всегда имеете возможность оценить
теплоемкость твердого вещества при
комнатной температуре, пользуясь только
таблицей Менделеева).
что
видно из таблицы. (Таким образом, вы
всегда имеете возможность оценить
теплоемкость твердого вещества при
комнатной температуре, пользуясь только
таблицей Менделеева).
Таблица 22.1
Температуры Дебая некоторых веществ.
Вещество |
, К |
Вещество |
, К |
Li |
354 |
Mo |
259 |
Be |
1160 |
W |
388 |
Al |
423 |
Ta |
247 |
Ti |
426 |
Ag |
228 |
Fe |
457 |
Au |
165 |
Ni |
476 |
Pt |
234 |
Cu |
342 |
Pb |
102 |
С
ростом температуры разность
![]() увеличивается, причем, как правило,
значительно сильнее, чем можно было бы
ожидать, основываясь на вышеприведенном
выражении. Это связано с тем, что с
повышением температуры колебания атомов
в узлах кристаллической решетки все
более отличаются от гармонических и
появляется дополнительный «ангармонический»
вклад в
увеличивается, причем, как правило,
значительно сильнее, чем можно было бы
ожидать, основываясь на вышеприведенном
выражении. Это связано с тем, что с
повышением температуры колебания атомов
в узлах кристаллической решетки все
более отличаются от гармонических и
появляется дополнительный «ангармонический»
вклад в
![]() ,
а для металлов становится существенной
теплоемкость «газа» электронов
проводимости. Электронная теплоемкость
меняется с температурой почти линейно
,
а для металлов становится существенной
теплоемкость «газа» электронов
проводимости. Электронная теплоемкость
меняется с температурой почти линейно
![]() .
Коэффициент
.
Коэффициент
![]() имеет величину порядка нескольких
мДж/(мольК2)
и
имеет величину порядка нескольких
мДж/(мольК2)
и
![]() становится сопоставимым с
только при достаточно высоких температурах
(а также при очень низкой температуре,
когда
становится сопоставимым с
только при достаточно высоких температурах
(а также при очень низкой температуре,
когда
![]() и
и
![]() .
Вид температурной зависимости
ангармонической составляющей колебательной
теплоемкости в настоящее время не
установлен.
.
Вид температурной зависимости
ангармонической составляющей колебательной
теплоемкости в настоящее время не
установлен.
При
очень высоких температурах, а также
вблизи температур структурных и фазовых
превращений появляются и другие
составляющие теплоемкости. В результате
вид
![]() в широком температурном интервале может
быть весьма сложным. В качестве примера
на рис. 22.1 приведена температурная
зависимость
железа.
в широком температурном интервале может
быть весьма сложным. В качестве примера
на рис. 22.1 приведена температурная
зависимость
железа.
