§91. Інтерференція світла у тонких плівках

Прикладом інтерференції світла, що спостерігається в природних умовах, може бути райдужне забарвлення мильних плівок, тонких плівок нафти або мінерального масла, які плавають на поверхні води, кольори мінливості на поверхні загартованих стальних деталей, покритих найтоншим шаром оксидів. Усі ці явища зумовлені інтерференцією світла в тонких прозорих плівках, яка виникає внаслідок накладання когерентних хвиль, що відбиваються від верхньої та нижньої поверхонь плівки.

Нехай плоска монохроматична хвиля, поширюється у середовищі з показником заломлення , (рис. 212), падає під кутом і на плоскопаралельну прозору плів­ку з показником заломлення n і товщиною d.

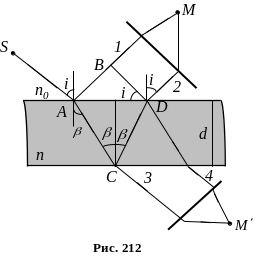
Падаюча хвиля частково відбивається від верхньої поверхні плівки та част­ково заломлюється. Напрямок поширення відбитої хвилі зображено променем AB, а заломленої – променем AС. Заломлена хвиля, досягнувши нижньої поверхні плівки, частково відбивається (промінь СD), і частково заломлюється. Хвиля, що поширюється вздовж променя СD, на верхній поверхні плівки частково відбивається, і частково заломлюється, причому заломлена хвиля (промінь 2) накладається на хвилю, що безпосередньо відбита від верхньої поверхні.

Промені 1 і 2 когерентні між собою, оскільки вони утворені поділом хвилі SA. Якщо на їх шляху поставити збірну лінзу, то вони зберуться в одній з точок М фо­кальної площини лінзи і дадуть інтерфе­ренційну картину, яка визначається оптичною різницею ходу між променями 1 і 2:

.

Тут прийнято, що показник заломлення . Доданок зумовлений втратою півхвилі при відбиванні світла на межі поділу середовищ. Якщо , то в точці A фаза коливань змінюється на протилежну, відбувається втрата півхвилі і доданок матиме знак „–“. У випадку втрата півхвилі відбудеться в точці C і матиме знак „+”.

З рис. 212 видно, що

, .

Оскільки або , то . Тоді:

.

З урахуванням втрати півхвилі для оптичної різниці ходу отримаємо:

.

В точці M буде максимум, якщо:

і мінімум, якщо:

Інтерференція спостерігається не лише у відбитому світлі, а й у світлі, що проходить через плівку (рис. 212, промені 3 і 4). Оптична різниця ходу для прохідного світла відрізняється від для відбитого світла на , бо світло не відбивається від оптично густішого середовища. Отже, мак­симумам інтерференції у відбитому світлі відповідають мінімуми інтерференції в прохідному світлі і навпаки.

1. Смуги однакового нахилу

Інтерференція світла в плоскопаралельних пластинках визначається товщиною пластинки d, показником заломлення n середовища, довжиною падаючої світлової хвилі та кутом падіння і. Для даних , d i n кожному куту i падіння променів відповідає своя інтерференційна смуга.

Інтерференційні смуги, які виникають внаслідок накладання хвиль, що падають на плоскопаралельну пластинку під однаковими кутами, називаються смугами однакового нахилу.

Промені і , відбившись від верхньої та нижньої граней пластинки, паралельні один до одного, оскільки пластина плоскопаралельна (рис. 213).

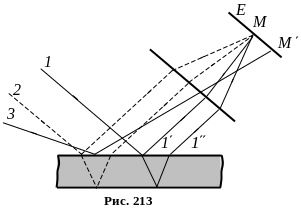
Отже, інтерферуючі промені і перетинаються лише в нескінченності, тому кажуть, що смуги однакового нахилу локалізовані в нескінченності.

Для їх спостереження використовують збірну лінзу й екран, розміщений у фокальній площині лінзи. Паралельні промені і зберуться у фокусі лінзи. В ту саму точку прийдуть й інші промені, паралельні до променя 1, (на рис. 213 – промінь 2) внаслідок чого збільшиться загальна інтенсивність.

Хвилі 3, які падають на пластину під іншим кутом, зберуться в іншій точці фокальної площини лінзи.

Оцінимо допустиму товщину пластинки, при освітленні якої природним світ­лом, можна спостерігати інтерференційну картину. Щоб світлові хвилі інтерферували, необхідно щоб виконувалась часова когерентність, а саме різниця ходу променів Δ повинна бути меншою за довжину когерентності :

або

.

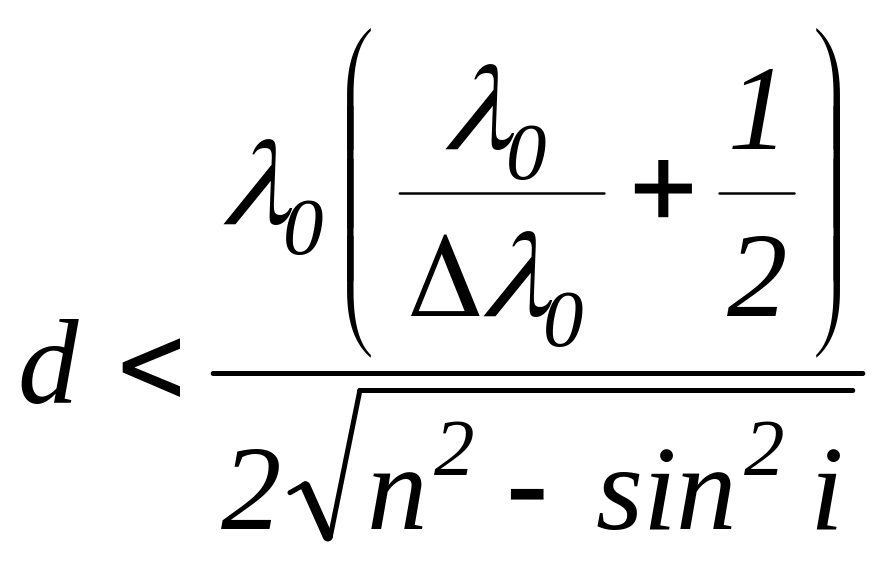Нехай довжина падаючого світла і . Саме з такою різницею хвиль людське око здатне розрізняти дві спектральні лінії. Тоді . Нехтуючи величиною в порівняння з , отримуємо

.

Для n=1,5 та кута падіння дістаємо

.

В результаті

.

Якщо ступінь монохроматичності світла збільшується ( – досить мале), то допустима товщина пластинки буде зростати.