
- •1. Общая характеристика растворов. Способы выражения состава растворов.
- •2.Формальная кинетика обратимых реакций второго порядка.
- •1. Парциальные молярные величины. Физический смыл пмв. Уравнение Гиббса-Дюгема и Дюгема-Маргулиса. Методы определения пмв.
- •1. Термодинамика процессов замерзания и кипения для идеальных и бесконечно разбавленных растворов (общий вид уравнений).
- •2. Теория активированного комплекса. Физический смысл координаты реакции. Трансмиссионный коэффициент, энтальпия и энтропия активации.
- •1. Реальные и регулярные растворы. Положительные и отрицательные отклонения от закона рауля.
- •2. Формальная кинетика простых реакций n–го порядка
- •1. Закон распределния растворенного вещества.
- •2. Внешняя массопередача. Коэффициент массопередачи.
- •1. Теория электролитической диссоциации.
- •2. Адсорбция газов. Изотерма лангмюра.
- •1. Электропроводимость. Подвижность ионов. Числа переноса.
- •1. Электропроводимость. Подвижность ионов. Числа переноса.
- •2. Адсорбция на неоднородной поверхности. Изотерма темкина.
- •1. Методы определения активности.
- •2. Формальная кинетика простых реакций первого порядка.
- •1. Закономерности давления насыщенного пара растворенного вещества(з-ны генри и сивертса). Закономерности давления насыщенного пара растворителя.
- •2. Микро и макро системы. Законы Максвелла и Максвелла – Больцмана.
- •1. Теория сильных электролитов.Ионная сила раствора.
- •2. Формальная кинетика простых реакций n-го порядка.
- •1. Адсорбция на поверхности жидкости.
- •2. Теория активных соударений аррениуса. (тас).
- •1. Эдс гальванического элемента. Зависимость эдс от т. Термодинамика гэ.
- •2. Формальная кинетика простых реакций второго порядка.
- •1. Осмос.Осмотическое давление.
- •2. Методы определения порядка реакции.
- •1.Равновесные элктродные потенциалы. Водородный электрод.
- •2. Влияние температуры на скорость реакции. Температурный коэффициент.
- •1. Классификация электродов.
- •1. Классификация растворов. Связь химического потенциала компонента с составом раствора для совершенных, разбавленных и реальных растворов.
- •2. Кинетическая классификация реакций. Молекулярность и порядок реакции.
- •1. Типы гальванических элементов.
- •2. Формальная кинетика простых реакций третьего порядка.
1. Осмос.Осмотическое давление.
Осмос – явление
самопроизвольного перехода растворителя
в раствор, который отделен от него
полупроницаемой перегородкой (мембраной).
Осмос наблюдают в специальных приборах
(осмометрах). Устройство простейшего
осмометра: (см.рис)
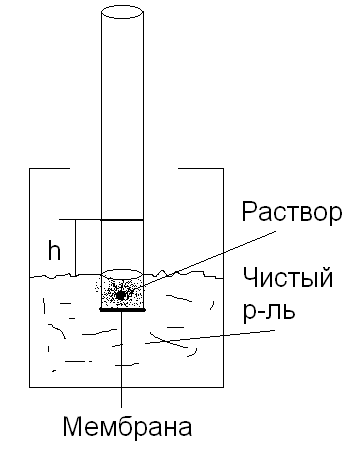 .
При опускании трубки с раствором в сосуд
с растворителем уровень жидкости в
трубке поднимается на некоторую высоту
h.
Гидростатическое давление столба
жидкости высотой h
в состоянии равновесия называется
Осмотическим давлением и количественно
характеризует осмос. Изучая это явление
на бесконечно разбавленных растворах
Вант - Гофф установил закон: π = СRT
– для неэлектролитов. π = iСRT
– для электролитов, где С – молярная
концентрация (моль/дм3), R
= 8.314 (дж/моль К) Т – температура, i
– изотонический коэффициент, который
характеризует во сколько раз общая
концентрация частиц растворенного
вещества электролита ( под частицами у
неэлектролитов – молекулы, у электролитов
– сумма молекул и ионов) превышает
расчетную молярную концентрацию.
Растворы разных веществ при одинаковом
значении концентрации С и Т будут
обладать одинаковым осмотическим
давлением. Такие растворы называются
изотоничными. Термодинамика осмотического
давления: Рассмотрим систему представляющую
собой герметичный сосуд с откачанным
воздухом. Полость сосуда не полностью
разделена полупроницаемой перегородкой.
В одну часть сосуда помещают растворитель,
а в другую – раствор. Из-за осмоса будем
наблюдать: (см. рис)
.
При опускании трубки с раствором в сосуд
с растворителем уровень жидкости в
трубке поднимается на некоторую высоту
h.
Гидростатическое давление столба
жидкости высотой h
в состоянии равновесия называется
Осмотическим давлением и количественно
характеризует осмос. Изучая это явление
на бесконечно разбавленных растворах
Вант - Гофф установил закон: π = СRT
– для неэлектролитов. π = iСRT
– для электролитов, где С – молярная
концентрация (моль/дм3), R
= 8.314 (дж/моль К) Т – температура, i
– изотонический коэффициент, который
характеризует во сколько раз общая
концентрация частиц растворенного
вещества электролита ( под частицами у
неэлектролитов – молекулы, у электролитов
– сумма молекул и ионов) превышает
расчетную молярную концентрацию.
Растворы разных веществ при одинаковом
значении концентрации С и Т будут
обладать одинаковым осмотическим
давлением. Такие растворы называются
изотоничными. Термодинамика осмотического
давления: Рассмотрим систему представляющую
собой герметичный сосуд с откачанным
воздухом. Полость сосуда не полностью
разделена полупроницаемой перегородкой.
В одну часть сосуда помещают растворитель,
а в другую – раствор. Из-за осмоса будем
наблюдать: (см. рис)
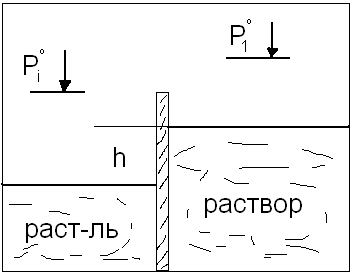 .
Рi0<P1.
Равновесие в такой системе с точки
зрения термодинамики следует
характеризовать равенством хим
потенциалов всех компонентов во всех
фазах. Для растворителя: (1)
μ1
= μ10,
где μ1
– хим потенциал растворителя в растворе,
μ10-
хим потенциал растворителя в чистом
растворителе. μ1
= f
(π, N1),
μ10
= const.
Следовательно, продифференцировав (1)
при постоянстве Т, получим: (б μ1/б
π)Т,N1*d
π + (б μ1/б
N1)Т
,π *d
N1
= 0. Из параграфа ТХФ известно, что (бG/бР)Т
= V.
Заменим G
на μ1,
Р на π, V
на V
(с чертой). Тогда после преобразований
получим: d
π/dN1
= – ((б μ1/бN1)
Т ,π )/
V1
(c
чертой). –
основное термодинамическое уравнение
для осмотического давления.
.
Рi0<P1.
Равновесие в такой системе с точки
зрения термодинамики следует
характеризовать равенством хим
потенциалов всех компонентов во всех
фазах. Для растворителя: (1)
μ1
= μ10,
где μ1
– хим потенциал растворителя в растворе,
μ10-
хим потенциал растворителя в чистом
растворителе. μ1
= f
(π, N1),
μ10
= const.
Следовательно, продифференцировав (1)
при постоянстве Т, получим: (б μ1/б
π)Т,N1*d
π + (б μ1/б
N1)Т
,π *d
N1
= 0. Из параграфа ТХФ известно, что (бG/бР)Т
= V.
Заменим G
на μ1,
Р на π, V
на V
(с чертой). Тогда после преобразований
получим: d
π/dN1
= – ((б μ1/бN1)
Т ,π )/
V1
(c
чертой). –
основное термодинамическое уравнение
для осмотического давления.
2. Методы определения порядка реакции.
I.
Интегральные методы: 1)
Способ подстановки. Полученные
экспериментальные данные подставляют
в уравнение для расчета константы
скорости реакции различных порядков.
В каком случае по ряду из экспериментальных
данных получится примерно одинаковые
значения k,
следовательно, тот порядок и есть. 2)
Графический способ. По экспериментальным
данным строят графики зависимости в
координатах: n=1
ln(a
– x)
= f(τ),
n=2
1/(a
– x)
= f(τ),
n=3
1/(a
– x)2
= f(τ).
На каком из графиков экспериментальные
точки ложатся на прямую линию –
следовательно, тот порядок и есть. 3)
По периоду полупревращения. Если τ1/2
не = f(a)
то n=1,
если τ1/2
= f(1/a),
то n=2,
и если τ1/2
= f(1/a2),
то n=3.
II.
Дифференциальный метод Вант Гоффа.
Начальные
концентрации реагентов берутся
одинаковыми. Проводят эксперимент, в
котором определяют концентрации
реагентов в различные промежутки
времени. По полученным данным строят
график зависимости концентрации от
времени: (a
– x)
= f(τ).(см.рис)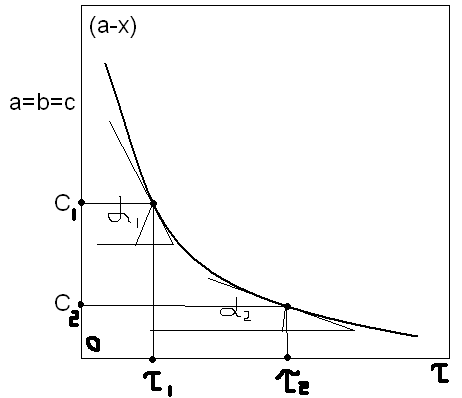 .По
графику при двух разных τ
определена скорость реакции. υ1
= – tgα1,
υ2
= – tgα2.
Таким образом порядок реакции можно
определить: n=(lnυ2
– lnυ1)/(lnC2
– lnC1).
Из этой формулы следует, что порядок
реакции можно определить по графику:
lnυ
= f(lnC).
(см.рис)
.По
графику при двух разных τ
определена скорость реакции. υ1
= – tgα1,
υ2
= – tgα2.
Таким образом порядок реакции можно
определить: n=(lnυ2
– lnυ1)/(lnC2
– lnC1).
Из этой формулы следует, что порядок
реакции можно определить по графику:
lnυ
= f(lnC).
(см.рис)![]() .
tgα
= n.
III.
Определение порядка реакции по τ1/2.
1)Для
реакции n-го
порядка (кроме первого), можно использовать
формулу: τ1/2
= (2n-1
– 1)/(n-1)(kan-1),
из эксперимента определяют k,
a,
τ1/2.
Выражают n
и находят. 2)
Способ Оствальда – Нойеса. Используется
для любого порядка (кроме первого). Т.к.
период полупревращения зависит от
исходной концентрации веществ и между
ними выполняется соотношение: (а2/а1)n-1
= (τ1/2)1/(τ1/2)2,
после интегрирования и необходимых
преобразований получается: n
= [ln(τ1/2)1
- ln(τ1/2)2]
/ [lna2
– lna1]
+ 1. [Единица прибавляется ко всей
дроби!!!).
.
tgα
= n.
III.
Определение порядка реакции по τ1/2.
1)Для
реакции n-го
порядка (кроме первого), можно использовать
формулу: τ1/2
= (2n-1
– 1)/(n-1)(kan-1),
из эксперимента определяют k,
a,
τ1/2.
Выражают n
и находят. 2)
Способ Оствальда – Нойеса. Используется
для любого порядка (кроме первого). Т.к.
период полупревращения зависит от
исходной концентрации веществ и между
ними выполняется соотношение: (а2/а1)n-1
= (τ1/2)1/(τ1/2)2,
после интегрирования и необходимых
преобразований получается: n
= [ln(τ1/2)1
- ln(τ1/2)2]
/ [lna2
– lna1]
+ 1. [Единица прибавляется ко всей
дроби!!!).
1. Вычислите среднюю ионную моляльность и ионную силу раствора хлорида натрия, если средний ионный коэффициент активности соли в растворе равен 0,902.
Дано: NaCl; γ±=0,902; Найти m±-? I-? Решение: 1) lnγ±=-0,509∙z+∙z-∙√I; z+=z-=1; lnγ±=-0,509∙√I; √I=-0,1/-0,509; I=0,196²=0,0385; 2) I=1/2(m+z+²+m-z-²)=1/2 (m+ + m-); m=0,0385 моль/кг; m±=m (υ+^υ+ ∙ υ-^υ-) ^1/υ=m^1/2=0,196;
2. При 298 К константа скорости реакции второго порядка равна 0,056 с^-1•л/моль. Определите т1/2 для компонента В, если в начальный момент времени смешали 250 мл 0,25 М раствора А и 500 мл 0,05 М раствора В.
Дано: k=0,056 с^-1•л/моль;T=298К; n=2; V1=250 мл; C1=0,25М; V2=500мл; C2=0,05М; Найти т1/2-? Решение: а=С1∙V1/V1+V2=250∙0,25/250∙500=0,0825; b=C2∙V2/V1+V2=0,05∙500/750=0,033; x=b/2=0,033/2=0,0165; т1/2=1/k(a-b) ∙ ln b(a-x)/a(b-x)=1/0,056 (0,0825-0.033) ∙ ln 0,33(0,0825-0,0165)/0,0825(0,033-0,0165)=1000,2 cек.
БИЛЕТ 16.
