26. Привязки теодолитного хода к двум одинарным стенным знакам

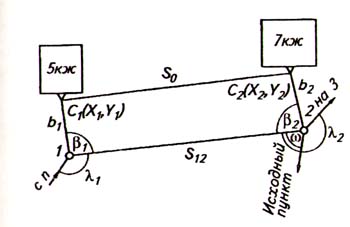
Для реализации этого способа выполняют следующие дей­ствия:

выбирают две смежные точки 1 и 2 теодолитного хода против одинарных стенных знаков С₁ и С₂ с таким рас­четом, чтобы горизонтальные углы β₁ и β₂ были бы в пределах 88…92°, а длины горизонтальных сторон b₁ и b₂ не превышали 20 м;

измеряют горизонтальные углы β₁ и β₂, горизонтальное рассто­яние S₁₂ между точками 1 и 2, а также стороны b₁ и b₂;

вычисляют по исходным координатам (Х₁ Y₁ Х₂, Y₂) соответ­ственно стенные знаки С₁ и С₂, горизонтальное положение S₀ между ними и дирекционный угол α_C1-C2 линии С₁С₂;

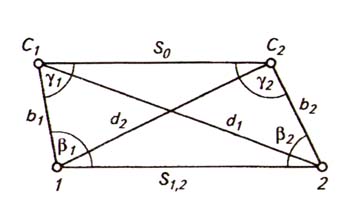
вычисляют по формулам  углы γ₁ и γ₂ четыреху­гольника 1 С₁С₂2 а именно:

d²₁ = b²₁ + S²_1,2 – 2b₁S_1,2cos β₁,

d²₂ = b²₂ + S²_1,2 – 2b₂S_1,2cos β₂,

γ₁ = arccos[(b²₁ + S²₀ – d²₂)/2b₁S₀],

γ₂ = arccos[(b²₂ + S²₀ – d²₁)/2b₂S₀];

находят для контроля вычислений сумму внутренних углов че­тырехугольника 1С₁С₂ 2, которая должна быть равна 360°;

устанавливают от стенного знака С₁, решая прямую геодезическую задачу, координаты точки 1:

X₁ = X_C1 + b₁ cos(α_C1-C2 + γ₁),

Y₁ = Y_C1 + b₁ sin(α_C1-C2 + γ₁),

Аналогично вычисляют координаты точки 2:

X₂ = X_C2 + b₂ cos(α_C1-C2 – γ₂ + 180°),

Y₂ = Y_C2 + b₂ sin(α_C1-C2 – γ₂+ 180°),

выполнить заключительный контроль вычислений следующим образом: используя вычисленный дирекционный угол α_1,2, реша­ют прямую геодезическую задачу по направлению 2 С₂ и вычисля­ют координаты стенного знака С₂. Затем сравнивают полученные значения с исходными координатами. Расхождения в этих коор­динатах не должны превышать 1 см.

27. Привязка хода способом прямых угловых засечек.

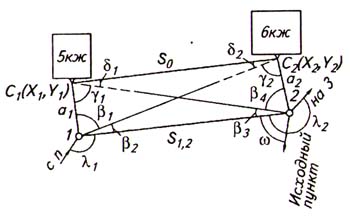
Для выполнения работ: выбирают две смежные точки 1 и 2 теодолитного хода против одинарных стенных знаков С₁ и С₂;

измеряют на точках 1 и 2 горизонтальные углы β₁, β₂, β₃ и β₄, a также все углы теодолитного хода (правые или левые);

измеряют горизонтальное проложение S₁₂ между точками 1 и 2.

Вычисляют плоские прямоугольные координаты Х₁ Y₁ и Х₂ Y₂ со­ответственно точек 1 и 2 в такой последовательности:

находят, решая треугольники 1C₁2 и 1С₂2 по теореме синусов:

горизонтальные расстоя­ния a₁ и а₂ соответственно от точек 1 и 2 теодолитного хода до стенных знаков С₁ и С₂:

a₁ = (S_1,2 sin β₃/sin γ₁),

a₂ = (S_1,2 sin β₂/sin γ₂),

где γ₁ = 180° – (β₁ + β₂ + β₃); γ₂ = 180° – (β₂ + β₃ + β₄);

находим по заданным координатам стенных   знаков, решая обратную геодезическую задачу, дирекционный угол α_C1C2 линии С₁С₂2 и ее горизонтальное проложение S₀;

находят по теореме синусов из треугольников C₁C₂2 и С₁С₂1 соответственно горизонтальные углы δ₁ и δ₂;

находят значения искомых координат Х₁Y₁ и X₂Y₂ соответствен­но точек хода 1и 2 теодолитного хода от одинарных стенных зна­ков С₁ и С₂, решая соответствующие прямые геодезические зада­чи. Например, координаты точки 1 можно вычислить по форму­лам:

X₁ = X_C1 + a₁cos(α_C1C2 + δ₁γ₁),

Y₁ = Y_C1 + a₁sin(α_C1C2 + δ₁γ₁).

Аналогично можно вычислить плоские прямоугольные коорди­наты точки 2, приняв за исходные координаты пункта С₂, а также найденные значения углов γ₂ и δ₂;

ориентируют теодолитный ход и контролируют определение координат точек 1 и 2.