7.3 Многослойная цилиндрическая стенка

Дано: ____n

d₁, d₂, d₃, ..., d_n, d_n+1

t_ж1

t_ж2

t_cn

t_c(n+1)



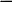
R_l = 1 +_ ln(d_(i+1)/d_i) + 1

 ₁d₁ ₂d₂

k_l = 1 ;

1 +_ ln(d_(i+1)/d_i) + 1 ;

 ₁d₁ ₂d₂

Примечание 1:  = const, но _t=_(1+bt)

t_c1, t_c2 ГУI, то  = const t_ср = (t_c1 + t_c2)/2

t_ж1, t_ж2 ГУIII, то t_ср = (t_ж1 + t_ж2)/2

если  ₁не равен ₂ , то появляется погрешность.

Примечание 2:

z

t₁

t₂

x

т.е. движется по одной и той же изометрической поверхности.

по направлению оси z температура не меняется.

8. Обобщенный метод решения задач теплопроводности при стационарном тепловом режиме

Q = - F , Вт - закон Фурье

q = - , Вт/м²

qdx = -dt x=x₁ t = t_c1

x=x₂ t = t_c2

x₂ - x₁ =

q = -

q(x₂ - x₁) = - (t_c2 - t_c1) t_c1 > t_c2

t_c1 - t_c2 = q /

t_c2 = t_c1 - q /

Представим себе стенку произвольной кривизны с замкнутыми поверхностями; сферическая - очевидно, плоскую стенку будем считать сферической с радиусом кривизны, устремленным в бесконечность.

Q = - F(n)

F(n) - поверхность, как функция от нормали.

пусть J_n1ⁿ² = , тогда

(*) = J_n1ⁿ²

t₂ = t₁ - J_n1ⁿ²

Рассмотрим 3 классических стенки:

1. Плоская: n = x, n₁ = x₁, n₂ = x₂, F(n) = const

J_n1ⁿ² =

t₂ = t₁ -

t₂ = t₁ - q

J_n1ⁿ² - относительная или удельная толщина стенки.

2. Цилиндрическая: F(n) = 2 lr = dl ; n r

J_n1ⁿ² =

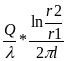
t₂ = t₁ - q_l - пагонная плотность теплового потока.

t_ = t₁ - q_l

3. Шаровая: n r, n₁ = r₁, n₂ = r_2, F(n) = 4 r²

J_n1ⁿ² =

t₂ = t₁ -

4. Уравнение для любой точки произвольной стенки:

t = t₁ - J_n1ⁿ²

из (*)

t = t₁-

,

где X - стенки любой кривизны

X_{плоской стенки} =

X_{цилиндр.стенки} =

9. Критический диаметр цилиндрической стенки

α₂

α₁

d₂

d₁

d₁ = const; d₂ = var (переменная)

q _l = (t_ж1 - t_ж2) /R_l q_l уменьшение

1/2 d₂^экстр = 1/ ₂d₂^экстр

1/2 =1/ ₂d₂

2 = ₂d₂

d₂^экстр = 2 / _{2 _} +

d₂^экстр d₂

При увеличении d₂ вводится 2 ф-ла:

- теплопотери растут из-за увеличения наружной поверхности и убывают из-за того, что увеличивается термосопротивление стенки.

- левая область “-” считается нерабочей, этим явлением пользуются для выбора материала тепловой изоляции. Если при конструировании тепловой изоляции мы оказались в области “-”, то нужно выбрать материал с меньшим , d₂ не менять !

В плоской стенке увеличение толщины изоляции всегда приводит к снижению тепловых потерь.