Свойства уровенных поверхностей

• Уровенные поверхности можно проводить на разных высотах, все они являются замкнутыми и почти параллельны одна другой.

• Через одну точку пространства проходит только одна уровенная поверхность.

• Направление нормали к уровенной поверхности совпадает с направлением силы тяжести, то есть с отвесной линией.

Форма уровенной поверхности не имеет точного математического выражения и зависит от распределения масс различной плотности в теле Земли.

Земной эллипсоид (эллипсоид вращения)

Эллипсоид вращения – близкая по форме геоиду, но математически правильная поверхность, на которую можно перенести результаты измерений выполненных на физической поверхности Земли. Земной эллипсоид – эллипсоид вращавшийся вокруг своей малой оси. Чтобы на поверхности можно было работать, необходимо знать его основные параметры: 

a – большая полуось, a = OE, b – малая полуось, b = OP с – полярное сжатие, a = (a-b)/a, e – эксцентриситет,  . Для определения этих параметров выполняются градусные измерения, которые изначально сводились к определению длины дуги меридиана в 1 градус.

3. Географические координаты

Географические координаты – величины, определяющие положение точки на земной поверхности: широта B, измеряемая углом между отвесной линией в данной точке и плоскостью земного экватора, и долгота L, измеряемая двугранным углом между плоскостью меридиана данной точки и плоскостью начального меридиана (см. рис.). Широта и долгота определяются из наблюдений небесных светил с помощью угломерных инструментов, установленных с помощью уровня, и из сравнения местного времени, полученного из астрономических наблюдений, с всемирным временем. Географические координаты, так определённые, называются астрономическими координатами точки земной поверхности.

Широты отсчитываются от 0° до 90° по обе стороны от экватора, причём в Северном полушарии Земли они считаются положительными, в Южном – отрицательными. Долготы отсчитываются от начального меридиана от 0° до 360° либо к востоку (восточная долгота), либо к западу (западная долгота; по международному счёту – положительная). Применяется также система отсчёта от 0° до 180° к востоку и западу от начала меридиана.

По международному соглашению за начальный («первый», «нулевой») меридиан принят меридиан, проходящий через меридианный круг старой Гринвичской обсерватории в Гринвиче (Лондон) до её перевода в замок Хёрстмонсо. Прежде для этой цели служили в разное время меридианы островов Иерро (Канарские острова), Парижской и Берлинской обсерваторий и др. В России в 19 в. счёт долгот вёлся от меридиана Пулковской обсерватории.

4. Полярные и прямоугольные координаты

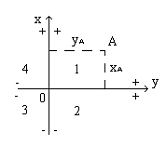
Прямоугольная система координат – система плоских координат образованная двумя взаимноперпендикулярными прямыми линиями, называемыми осями координат x и y. Точка их пересечения называется началом или нулем системы координат. Ось абсцисс – OX, ось ординат – OY.

Существуют две системы прямоугольных координат: левая и правая. В геодезии чаще применяется левая система. Положение точки в прямоугольной системе однозначно определяется двумя координатами X и Y; координата X выражает расстояние точки от оси ОY, координата Y – расстояние от оси OY.

Значения координат бывают положительные (со знаком "+") и отрицательные (со знаком "-") в зависимости от того, в какой четверти находится искомая точка.

П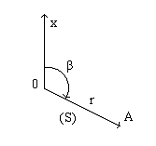 олярная система координат – система плоских координат образованная направленным прямым лучом OX, называющимся полярной осью. Чаще всего за полярную ось принимают ось северного направления какого-либо меридиана. Начало координат - точка O - называется полюсом системы.

Положение любой точки в полярной системе определяется двумя координатами: радиусом-вектором r (или полярным расстоянием S) – расстоянием от полюса до точки, и полярным углом b при точке O, образованным осью OX и радиусом вектором точки и отсчитываемым от оси OX по ходу часовой стрелки.

Под полярным углом b в геодезии часто принимают дирекционный угол направления, с помощью которого определяют координаты точек и расстояния между ними.

П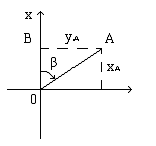 ереход от прямоугольных координат к полярным и обратно для случая, когда начала обеих систем находятся в одной точке и оси OX у них совпадают, выполняется по формулам прямой геодезической задачи:

tgb = Y/X,  b = arctg(Y/X)  

Эти формулы получаются из решения треугольника OBA по известным соотношениям между сторонами и углами прямоугольного треугольника. Системы прямоугольных и полярных координат применяются в геодезии для определения положения точек на плоскости.