
Определение
Множество всех х при которых функ. ряд (1) сх-ся (т.е. получаются сх-ся числ. ряды) наз-ся областью сходимости функ. ряда.
Определение
Если по любому заданному >0 можно указать n, т.ч. при всех n> n сразу для всех хЕ выполняется неравенство |Sn(x)-S(x)|<: (>0)( n):(n> n)(хЕ)[|Sn(x)-S(x)|= |rn(x)|<].
Геометрически: в случае сх-ти при n> n все графики у=Sn(x) целиком попадут в заданную полосу между графиками. В случае наравн. сх-ти какой бы n ни взять при n> n не удаётся заключить весь график у=Sn(x) в заданную полосу: всегда найдётся точка х Е т.ч. точка с координатами (х, Sn(x)) остаётся вне полосы.
Теор об остатке равном. сх-ся ряда.
Функ.
ряд (1) сходящийся на множестве Е (т.е.
сх-ся поточно) равном. сх-ся на Е
lim
![]() |rn(x)|
=0. Ряд (1)
сх-ся равномерно. Зададим >0,
по Опр.
(
n0):(n>
n0)(хЕ)[|rn(x)|<].
Это означает,
что 1
является верхней границей мн-ва {|rn(x)|:
xE},
а т.к. sup
– наим. Из верхних границ, то sup{|rn(x)|:
xE}1,
т.е.
|rn(x)|
=0. Ряд (1)
сх-ся равномерно. Зададим >0,
по Опр.
(
n0):(n>
n0)(хЕ)[|rn(x)|<].
Это означает,
что 1
является верхней границей мн-ва {|rn(x)|:
xE},
а т.к. sup
– наим. Из верхних границ, то sup{|rn(x)|:
xE}1,
т.е.
![]() |rn(x)|1
|rn(x)|=0.
lim
|rn(x)|=0.
Зададим
>0.
По условию (
n):(n>
n)[
|rn(x)|<(хЕ)[|rn(x)|<]]
(>0)(
n):(n>
n)(хЕ)[|rn(x)|<](опр
5.2.)
ряд(1)сх-ся равномерно на Е.
|rn(x)|1
|rn(x)|=0.
lim
|rn(x)|=0.
Зададим
>0.
По условию (
n):(n>
n)[
|rn(x)|<(хЕ)[|rn(x)|<]]
(>0)(
n):(n>
n)(хЕ)[|rn(x)|<](опр
5.2.)
ряд(1)сх-ся равномерно на Е.
Теор Критерий Коши равномерной сходимости функ. ряда.
Функ.
ряд (1) сх-ся на мн.Е равномерно
(>0)(n):(m>n>n)(xE)[|
![]() uk(x)|<]
uk(x)|<]
Пусть ряд (1) сх-ся равномерно. Зададим >0 и положим 1=/2, для него по Опр 5.2. ( n): (n> n)(хЕ)[|Sn(x)-S(x)|<1]. (m>n>n)(хЕ)[|Sn(x)-S(x)|<1]. Поэтому | uk(x)|= |Sm(x)-Sn(x)|= |(Sm(x)-S(x))+(S(x)-Sn(x))| |Sm(x)-S(x)|+|S(x)-Sn(x)|< 1+1=.
Пусть
выполнен критерий Коши. При конкр. хЕ
это означает выполнение кр. Коши для
числового ряда, значит ч.р.
un(x),
хЕ
сх-ся к некот. числу S(x).
Это означает, что ф.р. (1) поточеч. сх-ся
к некот. сумме S(x).
Осталось пок-ть, что это сх-ть равномерная.
Зададим >0
и возьмём 0<1<,
для него запишем кр. Коши: ( n0):
(
m>n>n0)
(хЕ)[
|
uk(x)|=
|Sm(x)-Sn(x)|<1].
Зафиксируем здесь n0
и х. И рассмотрим
![]() (при
этом всегда ост-ся m>n
и потому |Sm(x)-Sn(x)|<1
сохр. во всём процессе стремления m
к ).
В пределе получим (
n0):
(
m>n>n0)
(хЕ)[
|Sm(x)-Sn(x)|1],
но
|Sm(x)-Sn(x)|=|
Sm(x)
-
(при
этом всегда ост-ся m>n
и потому |Sm(x)-Sn(x)|<1
сохр. во всём процессе стремления m
к ).
В пределе получим (
n0):
(
m>n>n0)
(хЕ)[
|Sm(x)-Sn(x)|1],
но
|Sm(x)-Sn(x)|=|
Sm(x)
-
lim(n+)Sn(x)|=(*Sn(x)=const*)= |S(x)-Sn(x)|1 |Sn(x)-S(x)|<. Подчёркнутое означает, по Опр.5.2., что ряд (1) сх-ся равномерно на множестве Е. Из кр. Коши получается след. дост. признак равномерной сх-ти.
Теор Признак Вейерштрасса о равномерной сх-ти.
Если существует полож, числовой, сх-ся ряд an (4), т.ч. (n)(хЕ) [|uk(x)|an] (мажорирующий ряд, мажоранта), то ряд (1) сх-ся на множестве Е абсолютно и равномерно.
|uk(x)|an при всех хЕ следует, согл. признаку сравнения сх-ся |un(x)| un(x) сх-ся абсолютно на множестве Е. Для ряда (4) выполнен крит. Коши: (>0)(n):(m>n>n)
[| |<], но
Опр. Функ. ряд для которого сущ. мажоранта, наз-ся мажорирующим. По док-му ряд, мажорируемый на Е сх-ся абс-но и равномерно на мн-ве Е.
Свойства равномерно сх-ся рядов.
Известно, что конеч. сумма непрер-х функций, есть непр-я функ-я. Такую сумму можно почленно инт-ть, конеч. сумму диф-ть.
Для суммы функ. ряда это не так, например члены ряда x+(x2-x)+…+(xn-xn-1)+… непрер-ны на Е=[0,1], а сумма ряда S(x)={0, x[0,1[ и 1,x=1 разрывна в т. х=1.
Теор о непрерывности суммы ряда.
Если все члены un(x) функ. ряда u1(x)+u2(x)+…+un(x)+…(1) непрерывны на Е и ряд сх-ся равном. на Е, то S(x) непрер-на на Е.Надо пок-ть, что(х0Е) [S(x)c{x0}(>0)(>0): (xE,|x-x0|<)[S(x)-S(x0)<]]. Зададим >0 и положим 1=/3. Ввиду равном. сх-ти ряда для 1: ( n0):( n>n0) (хЕ)[|Sn(x)-S(x)|<1] (2). В частности |Sn(x0)-S(x)|<1 (3). Зафиксируем один номер n>n0 и рассм. функ-ю Sn(x)= u1(x)+…+un(x). Как конеч. сумма непр-х ф-ий она непр-на на Е. В частности Sn(x)c{x0}. Значит (>0):(xE,|x-x0|<)[Sn(x)-Sn(x0)<1] (4). Теперь из 2,4,3 получим |S(x)-S(x0)|=| (S(x)-Sn(x))+ (Sn(x)-Sn(x0))+( Sn(x0)-S(x0))| |Sn(x)-S(x)|+|Sn(x)-Sn(x0)|+|Sn(x0)-S(x0)|1+1+1=
Теор об интегрировании ряда.
Если
все члены un(x)
функ. ряда (1) непрер-ы на [a,b]
и ряд сх-ся на [a,b]
равномерно, то его можно почленно инт-ть
по любому отрезку [x1,x2][a,b].
![]() S(x)dx=
un(x)dx=
un(x)dx
(ряд
полученный почленным инт-ем ряда (1)
сх-ся и его сумма = интегралу от суммы
ряда (1) или интеграл от суммы ряда = сумме
ряда).
S(x)dx=
un(x)dx=
un(x)dx
(ряд
полученный почленным инт-ем ряда (1)
сх-ся и его сумма = интегралу от суммы
ряда (1) или интеграл от суммы ряда = сумме
ряда).
Т.к.
все un(x)[a,b],
то существует
un(x)dx=аn
(числа);
ввиду равном. сх-ти ряда по Теор.6.1. сумма
ряда S(x)[a,b]
сущ-ет
S(x)dx=
(число) и ост. док-ть, что числ. ряд
=
un(x)dx
сх-ся к ,
т.е. lim
![]() ak=.
Зададим
>0
и положим 1=/(х2-х1)>0.
Ввиду равном. сх-ти ряда (1) (n0):(
n>n0)
(х[a,b])[|Sn(x)-S(x)|<1]
(х[x1,x2])[|Sn(x)-S(x)|<1].
|
ak-|=
|
uk(x)dx
-
S(x)dx|
= (*для конеч.
суммы *
=|
(
uk(x)
– S(x))dx|
=|
(Sn(x)-S(x))dx|
|Sn(x)-S(x)|dx<
1dx=
1(x2-x1)=.
Т.о.
(>0)(n0):(
n>n0)[
|
ak-|<]
lim
ak=
ak=.
Зададим
>0
и положим 1=/(х2-х1)>0.
Ввиду равном. сх-ти ряда (1) (n0):(
n>n0)
(х[a,b])[|Sn(x)-S(x)|<1]
(х[x1,x2])[|Sn(x)-S(x)|<1].
|
ak-|=
|
uk(x)dx
-
S(x)dx|
= (*для конеч.
суммы *
=|
(
uk(x)
– S(x))dx|
=|
(Sn(x)-S(x))dx|
|Sn(x)-S(x)|dx<
1dx=
1(x2-x1)=.
Т.о.
(>0)(n0):(
n>n0)[
|
ak-|<]
lim
ak=
Теор о дифференцируемости ряда.
Если
все члены un(x)
ф.р. (1) сходящиеся на [a,b]
(необяз. равном.) непрер. диф-мы на [a,b]
(un(x)c[a,b]),
а ряд из производных: u1(x)+u2(x)+…+un(x)+…(5)
равномерно сх-ся на [a,b],
то ряд (1) можно почленно дифф-ть в любой
т.х[a,b]:
S(x)=(
un(x))=
un(x)
(производная
суммы ряда равна сумме производных).
По условию ряд (5) равном. сх-ся на [a,b]
к некот. сумме (х):
un(x)=
(х)
и по Теор.6.2. (*благодаря непрерывности
un(x)
на [a,b]*)
ряд (5) можно почленно инт-ть по отрезку
[a,x]
где х любая точка из [a,b]:
![]() (t)dt=
un(t)dt,
здесь
(t)dt=
un(t)dt,
здесь
un(t)dt
= un(t)![]() =
un(х)-
un(а).
Поэт.
(t)dt=
(un(х)-
un(а)).
Поскольку
un(х)
сх-ся к S(x)
по условию, в частности
un(а)
сх-ся к S(a),
по Теор Олин-х опер-ях с рядами 1.10.
(un(х)-
un(а))=
un(х)
-
un(а)
= S(x)-S(a),
а
след-но
(t)dt=
S(x)-S(a). По
Теор 6.1. сумма (х)
ряда (5) с непрерывными членами равномерно
сх-ся на [a,b]
непрер-на на [a,b].
Поэт. можно применить Т. о диф-ии инт-ла
с перем. верх. пределом: (
(t)dt)х=(х),
значит (х)=
S(x)
- 0
S(x)=
(х)=
un(х)
=
un(х)-
un(а).
Поэт.
(t)dt=
(un(х)-
un(а)).
Поскольку
un(х)
сх-ся к S(x)
по условию, в частности
un(а)
сх-ся к S(a),
по Теор Олин-х опер-ях с рядами 1.10.
(un(х)-
un(а))=
un(х)
-
un(а)
= S(x)-S(a),
а
след-но
(t)dt=
S(x)-S(a). По
Теор 6.1. сумма (х)
ряда (5) с непрерывными членами равномерно
сх-ся на [a,b]
непрер-на на [a,b].
Поэт. можно применить Т. о диф-ии инт-ла
с перем. верх. пределом: (
(t)dt)х=(х),
значит (х)=
S(x)
- 0
S(x)=
(х)=
un(х)
Теор об ограниченном множителе.
Если все члены ряда (1) равном. сх-ся на Е умножить на ф-ию ограниченную на Е, то равном. сх-ть ряда (1) на Е сохр-ся.
Пусть(хЕ)[|f(x)}M]. Рассм. ряд f(x)u1(x)+f(x)u2(x)+.. …+f(x)un(x)+…(6). Для равном. сх-ся ряда (1) вып-ся кр. Коши: (>0)(n):(m>n>n)(xE)[| uk(x)|<].
Тогда(xE)[ | f(x)uk(x)|=|f(x)|| uk(x)|M| uk(x)|<M(/M)=]. Поэт. для ряда (6) ок-ся выполненым кр-ий Коши:(>0)(n):(m>n>n)(xE)[| f(x)uk(x)|<] и потому он сх-ся равном. на Е.
Радиус сход-ти, интервал сход-ти, область сход-ти.
C0+C1(x-a)+C2(x-a)2+...+Cn(x-a)n+...==![]() Cn(x-a)n
(1), где Сn
и а - действительные числа, наз-ся
степенным рядом с центром х=а. Заменой
=х-а
такой ряд приводится к виду (вместо
пишем х):
Cn(x-a)n
(1), где Сn
и а - действительные числа, наз-ся
степенным рядом с центром х=а. Заменой
=х-а
такой ряд приводится к виду (вместо
пишем х):
С0+С1х+С2х2+...+Сnхn+...= Сnхn (2) поэтому можно ограничится изучением ряда (2). Ряд (2) всегда сходится к точке х=0: S(0)=C.
Т-ма Абеля
Если степенной ряд (2) сходится в точке х00, то он абсолютно сходится при х<х0, т.е. на ]-x0,x0[; если он расходится в точке х0 0, то расходится при х<x0, т.е. на ]-,-x0[ и ]x0,+[.
Если
сходится
![]() , то lim
, то lim
![]() и сходящаяся последовательность {
и сходящаяся последовательность {![]() }
ограничена: (n)[
M](n)[|Cn|
M/|x0n|.
Если |x|<|x0|,
то
=Cn|x|n
M/|x0n||x|n=
M(|x|/|x0|)n=
Mqn,
где q=|x|/|x0|<1.
Из сходимости геометрического ряда
Mqn
(q<1)
по признаку сравнения следует сход-ть
Сnxn,
т.е. абсолютная сход-ть ряда (2) при
рассматриваемом х<x0.
Eсли
ряд (2) расходится в точке х00,
то при х>x0
он не может сходится, т.к. по доказанному
он бы сходился в точке х0
при х>x0
ряд (2) расходится
}
ограничена: (n)[
M](n)[|Cn|
M/|x0n|.
Если |x|<|x0|,
то
=Cn|x|n
M/|x0n||x|n=
M(|x|/|x0|)n=
Mqn,
где q=|x|/|x0|<1.
Из сходимости геометрического ряда
Mqn
(q<1)
по признаку сравнения следует сход-ть
Сnxn,
т.е. абсолютная сход-ть ряда (2) при
рассматриваемом х<x0.
Eсли
ряд (2) расходится в точке х00,
то при х>x0
он не может сходится, т.к. по доказанному
он бы сходился в точке х0
при х>x0
ряд (2) расходится
Т-ма о радиусе сходимости
Для
каждого степенного ряда (2)сущ-ет
неотрицательное число R![]() такое, что на ]-R,R[ ряд абсолютно сходится,
а вне отрезка [-R,R]
(т.е. на ]-,-R[
u
]R,+[)
расходится.
такое, что на ]-R,R[ ряд абсолютно сходится,
а вне отрезка [-R,R]
(т.е. на ]-,-R[
u
]R,+[)
расходится.
Если
(2) ходится в единственной точке х=0, то
полагают R=0
(в точке х=0 ряд (2) сходится
абсолютно:
Сn0n=C0).
Пусть сущ-ют
![]() 0,
в которых ряд сходится, назовем их
точками сход-ти. Мн-во модулей точек
сход-ти обозначим Х={
},
и пусть R=Sup
X.
Т.к. имеются точки
0,
т.е.
>0,
то Sup
X>0,
т.е. R>0.
Пусть х<R,
тогда х
меньшее чем Sup
X
не может быть верхней границей мн-ва Х
и потому найдется
Х
такой, что
>x.
Из сход-ти (2) в точке
по т-ме Абеля следует абсолютная сход-ть
ряда в точке х. Таким образом ряд (2)
абсолютно сходится на ]-R,R[. В частности
если R=+,
то на ]-,+[.
Пусть R<+,
т.е. R-конечное
число, тогда если х>R,
то х не может быть точкой сход-ти, т.к.
для всех точек сход-ти
имеем
Sup
X=R
при х>R,
т.е. при х]-,-R[
u
]R,+[
ряд расходится.
0,
в которых ряд сходится, назовем их
точками сход-ти. Мн-во модулей точек
сход-ти обозначим Х={
},
и пусть R=Sup
X.
Т.к. имеются точки
0,
т.е.
>0,
то Sup
X>0,
т.е. R>0.
Пусть х<R,
тогда х
меньшее чем Sup
X
не может быть верхней границей мн-ва Х
и потому найдется
Х
такой, что
>x.
Из сход-ти (2) в точке
по т-ме Абеля следует абсолютная сход-ть
ряда в точке х. Таким образом ряд (2)
абсолютно сходится на ]-R,R[. В частности
если R=+,
то на ]-,+[.
Пусть R<+,
т.е. R-конечное
число, тогда если х>R,
то х не может быть точкой сход-ти, т.к.
для всех точек сход-ти
имеем
Sup
X=R
при х>R,
т.е. при х]-,-R[
u
]R,+[
ряд расходится.
Число R наз-ся радиусом сход-ти степенного ряда (2), ]-R,R[ -интервалом сходимости.
Замечание1.
Для степенного ряда (1) интервалом сход-ти явл-ся ]a-R,a+R[.
Если для Сnn ]-R,R[ -R< <R, т.е. -R<x-a<R a-R< x <a+R
Замечание2.
На концах интервала х=R ряд (2) может сходится (абсолютно или не абсолютно) и расходится, поэтому область сход-ти степенного ряда с точностью до граничных точек совпадает с интервалом сходимоси чтобы найти область сход-ти степенного ряда достаточно найти интервал сход-ти, а сход-ть в граничных точках х=R исследовать непосредственной подстановкой этих точек в ряд (2). Что же касается интервала сход-ти ряда (2), то он совпадает с интервалом сход-ти ряда из модулей Cnxn, т.к. внутри интервала сходимости ряд (2) сходится абсолютно, т.е. сходится ряд Cnxn, а вне интервала сход-ти ряд (2) расходится и тем более расходится ряд из модулей. Таким образом дело сводится к нахождению интервала сход-ти положительного ряда из модулей, а к этому положительному ряду можно применять признаки сход-ти положительных рядов.
Свойства степенных рядов.
Т-ма о равномерной сход-ти степенного ряда.
anxn = a0+a1x+a2x2+...+anxn+... (1). Степенной ряд (1) сходится равномерно в каждом замкнутом промежутке, расположенным внутри области сход-ти степеного ряда (1).
Считаем,
что R>0.
Если промежуток (-R*,R*)
замкнутый и целиком лежащий в интервале
]-R,R[,
то обязательно найдется -![]() и
,
расположенные соответственно в ]-R,R*[
и ]R*,R[
и
,
расположенные соответственно в ]-R,R*[
и ]R*,R[
![]() .
Eсли
an
.
Eсли
an![]() -
cходится,
тоan
M
-
cходится,
тоan
M![]()
![]() .
Обозначим
.
Обозначим
![]() =q
< 1. Мы получим ряд из членов убывающей
геометрической прогрессии. Воспользуемся
признаком Вейерштрасса M·
=q
< 1. Мы получим ряд из членов убывающей
геометрической прогрессии. Воспользуемся
признаком Вейерштрасса M·
![]()
![]() сходится
ряд равномерно на [-R*,+R*]
сходится
ряд равномерно на [-R*,+R*]
Одна
из формул определения радиуса сход-ти
R
степенного ряда (основанная
на признаке Даламбера):
![]()
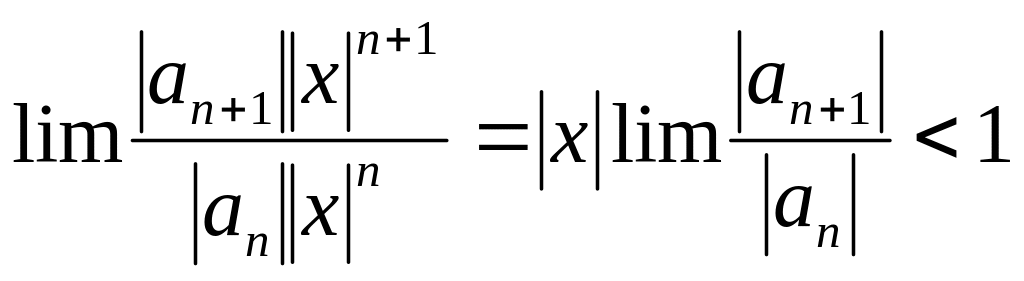 -
сходится.
-
сходится.
![]() (сходится )
х<R;
x>R
- расходится
(сходится )
х<R;
x>R
- расходится
Замечание: В общем случае этот предел может не существовать.
8.2. Т-ма
Внутри интервала сход-ти сумма ряда (1) - непрерывная функция.
Т.к. члены степенного ряда (1) непрерывные функции, то согласно т-ме о непрерывности суммы ряда, ряд (1) явл-ся непрерывной функцией
Т-ма об интегрируемости степенного ряда:
Пусть [x0,x1](-R,R), тогда
1)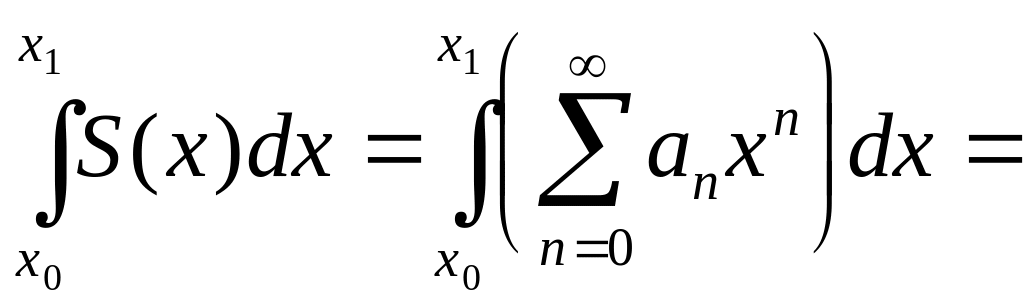
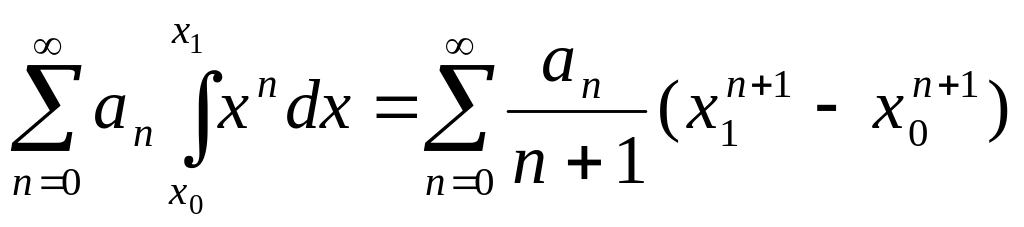 (2)
(2)
2) Радиус сход-ти ряда (2), полученного после интегрирования равен радиусу сход-ти исходного ряда (1).
Пусть
![]()
![]() (2*). Найдем радиус сход-ти ряда (2*).
(2*). Найдем радиус сход-ти ряда (2*).
![]()
Т-ма о дифференцируемости степенного ряда:
Внутри интервала сход-ти сумма степенного ряда S(x) - дифференцируемая функция, ряд можно почленно дифференцировать.
2)![]() Радиус
сход-ти степенного ряда, полученного
после дифференцирования, равен радиусу
исходного ряда.
Радиус
сход-ти степенного ряда, полученного
после дифференцирования, равен радиусу
исходного ряда.
1) Согласно предыдущей т-ме ряд сходится равномерно, члены дифференцируемы и по т-ме о дифференцируемости ряда ряд (1) можно дифференцировать почленно.
Рассмотрим ряд вида (S(x))’= ( anxn)=a1+2a2x+3a3x2+...+nanxn-1+..
Найдем
радиус сход-ти этого ряда
![]()
Формула Тейлора. Т-ма
Пусть функция f(x) имеет непрерывные производные вплоть до (n+1)- го порядка включительно в некоторой окрестности точки х=а, тогда имеет место формула Тейлора:
![]() .
Rn(x)
- остаточный член, который может быть
представлен в виде:
.
Rn(x)
- остаточный член, который может быть
представлен в виде:
![]() (2) - форма Лагранжа, где -расположена
между точками х и а. Другой вид:
(2) - форма Лагранжа, где -расположена
между точками х и а. Другой вид:![]()
Построим
вспомогательную функцию![]() (3)
(3)
тогда
(а)=f(x)(x)=f(x)+f
`(x)(x-x)+..=f(x)
(a)=f(x)
и (x)=f(x).
Тогда по т-ме Ролля найдется точка
в которой ’()=0.
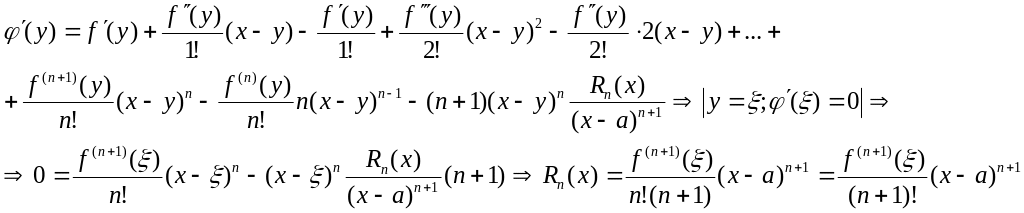 получим (2)
получим (2)
Замечания: 1) сущ-ют и другие представления Rn;
=a+(x-a), 1.
Ряды Тейлора и Макларена.
![]() ;
f(x)=Sn(x)+Rn(x)
(6); f(x)-Sn(x)=Rn(x)
(6).
Потребуем,
чтобы функция f(x)
имела бесконечное число производных
f(n)(x)
в точке x=а
и её окрестности. Получим: lim
(f(x)-Sn(x))=lim
Rn(x)=0
(7) . Если lim
Rn(x)
сущ-ет и равен 0, то f(x)=lim
Sn(x)
(8)
;
f(x)=Sn(x)+Rn(x)
(6); f(x)-Sn(x)=Rn(x)
(6).
Потребуем,
чтобы функция f(x)
имела бесконечное число производных
f(n)(x)
в точке x=а
и её окрестности. Получим: lim
(f(x)-Sn(x))=lim
Rn(x)=0
(7) . Если lim
Rn(x)
сущ-ет и равен 0, то f(x)=lim
Sn(x)
(8)
![]() (9)
- ряд Тейлора. При а=0 получаем ряд
Макларена:
(9)
- ряд Тейлора. При а=0 получаем ряд
Макларена:
![]() .
.
Замечание Функция представлена в форме ряда Тейлора в том случае если Rn(x)0.
Пример неразложимости функции в ряд Тейлора.
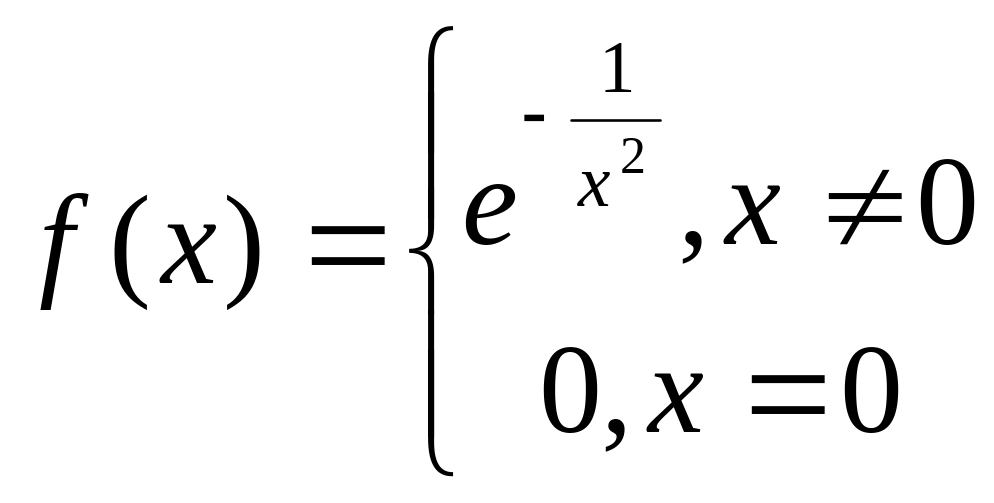 .
Т.к.
.
Т.к.
![]() =0,
то функция f(x)
непрерывная
=0,
то функция f(x)
непрерывная
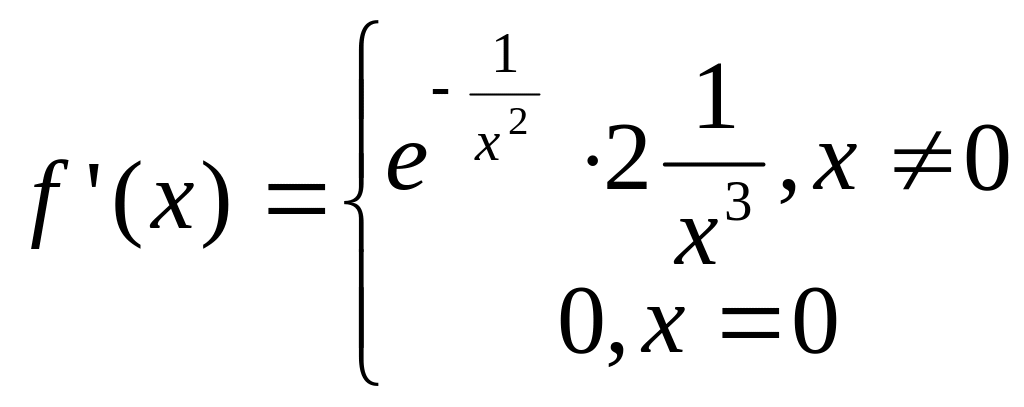
Обозначим
![]()
![]() .
По правилу Лопиталя
.
По правилу Лопиталя
![]()
Аналогичным образом устанавливается, что функция f(x) имеет бесконечно большое число производных и все они непрерывны на всей оси, включая точку х=0 и в точке х=0 обращаются в нуль.
n=0,1,2... Sn(x)=0. f(x)=Sn(x)+Rn(x)Rn(x) Rn(x)- не стремится к нулю, то ряда Тейлора для этой функции не сущ-ет.
Т-ма о представимости степенных рядов рядом Тейлора.
Если функция f(x) представима степенным рядом f(x)= an(x-a)n,
то
этот степенной ряд явл-ся рядом Тейлора
: f(x)=
![]() (x-a)n,
т.е. an=
(11). И такое разложение единственно и
коэфициенты нах-ся по формуле (11).
(x-a)n,
т.е. an=
(11). И такое разложение единственно и
коэфициенты нах-ся по формуле (11).
f
`(x)=
![]() nan(x-a)n-1,
f ``(x)=
nan(x-a)n-1,
f ``(x)=
![]() (n-1)nan(x-a)n-2,...,
f(i)(x)=
(n-1)nan(x-a)n-2,...,
f(i)(x)=![]() (n-i+1)(n-i+2)...nan(x-a)n-i
,
(n-i+1)(n-i+2)...nan(x-a)n-i
,
f(n)(a)=n!an (11). Докажем единственность: предположим противное и пройдя всю цепочку рассуждений получим все коэфициенты, которые определяются по формуле (11).
Т-ма (достаточный признак сход-ти степенного ряда к функции f или представимости в виде ряда Тейлора).
Пусть f(n)(x)C=const n=0,1,1... в некоторой замкнутой окрестности точки аХ, тогда функция f представима степенным рядом Тейлора.
Имеем
Rn(x)![]() (x-a)n+10
при n.
Применяя признак Даламбера получаем,
что ряд
(x-a)n+10
при n.
Применяя признак Даламбера получаем,
что ряд
(х-а)n+1 сходится
Разложение основных элементарных функций в степенные ряды.
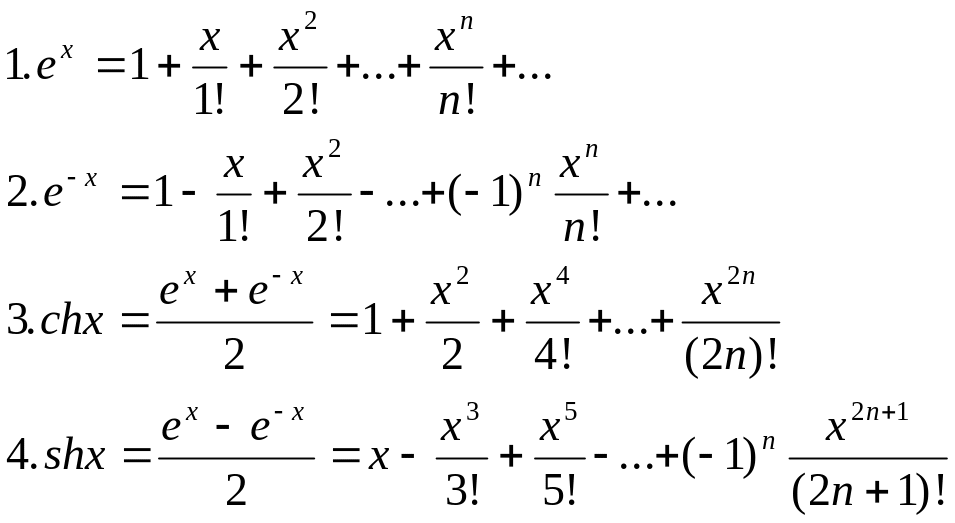
5.f(x)=cosx, f(0)=1,
(cosx)`=-sinx(0)=0,
(cosx)``(0)=(-cosx)(0)= -1
(cosx)```(0)=sinx(0)=0
(cosx)````(0)=cosx(0)=1,...
![]()
Т.к.
cosx-четная
функция, то сохраняются только четные
степени.
![]() .
Т.к. sin
и cos
по модулю 1,
то
.
Т.к. sin
и cos
по модулю 1,
то
![]()
![]() Остаточный
член оценивается точно так же как cos.
Указанные ряды можно использовать лишь
в окрестности точки х=0, при удалении от
х=0 апроксимация будет резко ухудшаться.
Остаточный
член оценивается точно так же как cos.
Указанные ряды можно использовать лишь
в окрестности точки х=0, при удалении от
х=0 апроксимация будет резко ухудшаться.
7.f(x)=ln(1+x)
ln(1+x)=
![]()
![]()
![]() ln(1+x)
ln(1+x)
8.f(x)=arctgx
![]()
![]()
![]()
9. Биномиальное разложение.
f(x)=(1+x), -любое действительное число.
f(0)=1; f `(0)=(1+x)-1=;
f ``(0)=(-1)(1+x)-2=(-1);
f ```(0)=(-1)(-2)(1+x)-3=
=(-1)(-2) ;...;
f(n)(0)=(-n+1)(1+x)-n=(-n+1).
 Определяем
остаточный член:
Определяем
остаточный член: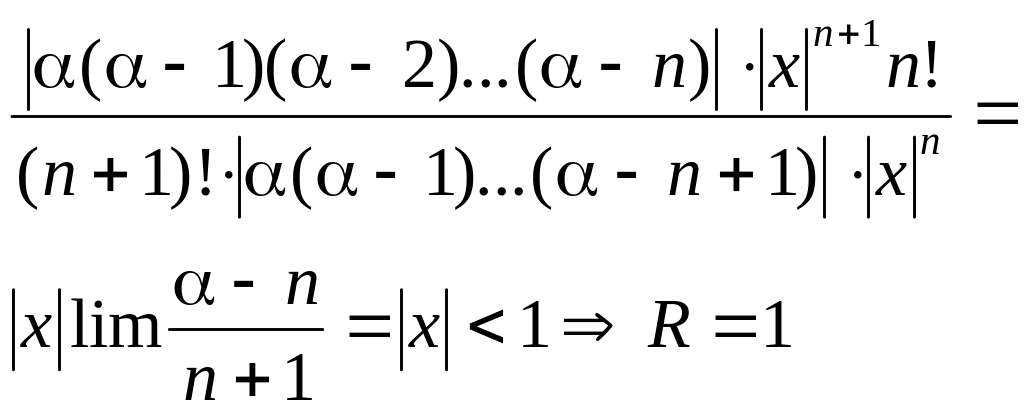

в точке х=0 S(x)=1
и f(x)=1
в точке х=0 S(x)=1
и f(x)=1
C=1.
Ряды Фурье.
Далее мы будем рассматривать глобальное разложение, то есть на конечном отрезке [a,b].
Определение. Понятие ортогонольных и нормированных систем ф-ий:
(х),
(х)
интегрируемые при х[a,b],
тогда
![]() (*)
- cкалярное
произведение.
(*)
- cкалярное
произведение.
для (*) вып-ся аксиомы ск-го произведения:
А.1 (,)=(,)
А.2 (,)=(,)=(,), =const
А.3 (,1+2)=(,1)+(,2)
Определение:
Функции
и
на [a,b]
ортогональны если (,)=0,
т.е.
![]() (х)(х)dx=0.
(х)(х)dx=0.
Определение.
Понятие нормированности:
=![]() - норма (длина вектора).
- норма (длина вектора).
Докажем, что норма обладает всеми св-вами длины:
=[ 2(x)dx]0.5
A.1 0, =0 0
A.2 =, R1
A.3 1+2=1+2
Определения: Если для системы функций 1,2,...,n введено понятие нормы, то такая система наз-ся нормированной. Если норма каждого элемента пространства равна 1, то наз-ся нормированной на 1. Если система функций попарно ортогональна и нормированная на 1, то такая система наз-ся ортонормированной: ОН - ортонормированная система, если
![]() ;
ОН
;
ОН ![]()
Пример: при x[-,]
{1,cosx,sinx,cos2x,sin2x,...,
cosnx,sinnx}.
![]()
![]()
![]() .
Аналогично
.
Аналогично
![]() sin(nx)sin(mx)dx=0;
sin(nx)cos(mx)dx=0.
Найдем норму: cosnx=
sin(nx)sin(mx)dx=0;
sin(nx)cos(mx)dx=0.
Найдем норму: cosnx=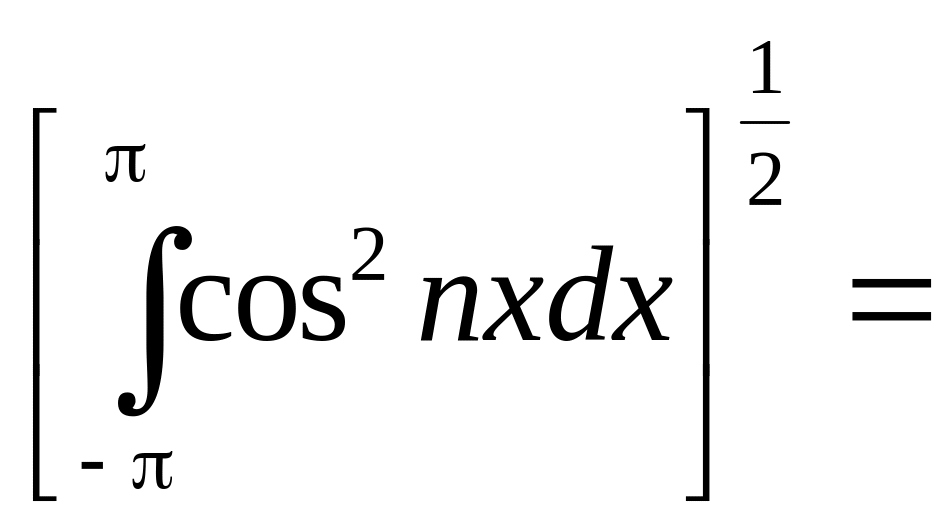
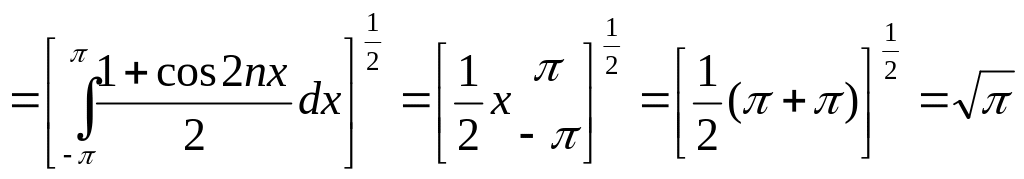 .
Аналогично
sin(nx)=
.
Аналогично
sin(nx)=![]() .Получаем
ОН систему:
.Получаем
ОН систему:
![]()
![]()
Ряд Фурье. Коэфициенты Фурье по ОН системе.
{1(x),2(x),...,n(x)}
- ОН система, т.е.
![]() .
f(x)=
.
f(x)=![]() fnn(x)
- ряд Фурье, где fn
- коэфициенты. Умножим обе части этого
уравнения на m(x)
и проинтегрируем:
fnn(x)
- ряд Фурье, где fn
- коэфициенты. Умножим обе части этого
уравнения на m(x)
и проинтегрируем:
f(x)m(x)dx== m(x) fnn(x)dx= fn m(x)n(x)dx=0 - когда mn. Когда m=n:
=fn(n,n)=fn= f(x)n(x)dx f(x) (f,n)n(x)
Ряд Фурье для тригонометрических функций.
,
f(x) ![]() (ancos(nx)+bnsin(nx))
(4)
(ancos(nx)+bnsin(nx))
(4)
где
an=![]() f(x)cos(nx)dx,
bn=
f(x)sin(nx)dx,
n=0,1,2,...
f(x)cos(nx)dx,
bn=
f(x)sin(nx)dx,
n=0,1,2,...
Определение: Функция наз-ся кусочно-непрерывной на данном отрезке, если этот отрезок можно разбить на конечное число интегралов, в каждом из которых функция непрерывна.
Т-ма Дирихле: Пусть f(x)
1)определена для всех х[-,]
2)кусочно-непрерывная на [-,]
3)кусочно-монотонная на [-,]
4)ограничена на [-,], тогда она разложима в тригонометрический ряд Фурье (4). Если точка х[-,] и в этой точки f(x) непрерывна, то сумма ряда
S(x)= (ancos(nx)+bnsin(nx))=f(x). Если точка х - точка разрыва, скачок, то S(x)=1/2 [f(x-0)+f(x+0)]
S(-)=S()=1/2 [f(+0)+f(-0)]
Замечания: 1)поведение функции f за пределами [-,] может в корне отличаться от значения S.
2)если мы хотим разложить f на всей действительной оси, то соглас- но (4) мы должны продол- жить пе- риодическим образом с периодом 2.
Пример: f(x)=x, x[-,]
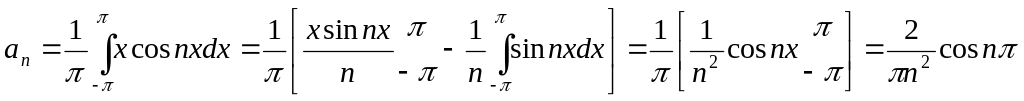
a0= xdx=0
![]()
Разложение функций в тригонометрические ряды на произвольном промежутке.
Часто возникает задача разложения функций в тригонометрический ряд на произвольном промежутке
y[a,b] (a,b < ,a < b)
x=y+; [-,] переходит в [a,b].
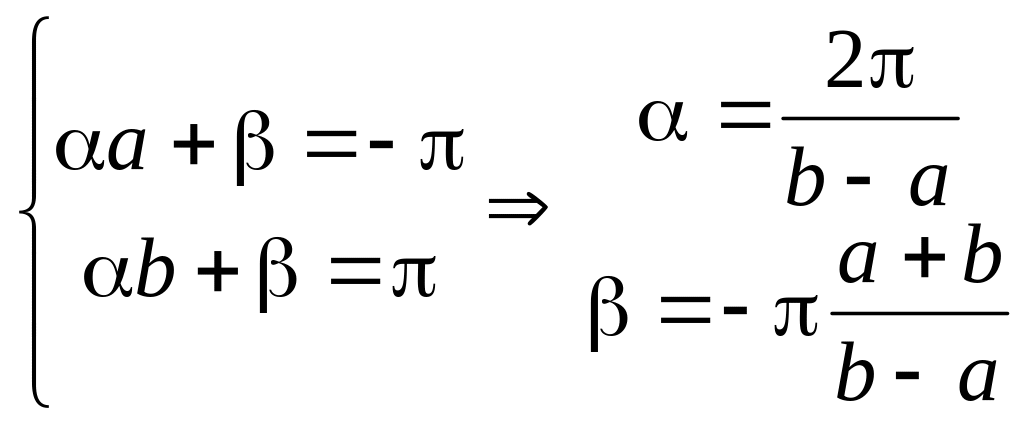 ,
,![]() m,
f(y+)=f*(y);
dx=dy,
an=
m,
f(y+)=f*(y);
dx=dy,
an=![]() f*(y)cosn(y+)dy
f*(y)cosn(y+)dy
bn=
f*(y)sinn(y+)dy,
f*(y)=![]() +
(ancosn(y+)+bnsinn(y+))
+
(ancosn(y+)+bnsinn(y+))
Разложив cos и sin по формулам:
f*(y)=![]() +
(a*ncosny+b*nsinny),
где нужно вычислить a*n
, b*n
и a*0
.
+
(a*ncosny+b*nsinny),
где нужно вычислить a*n
, b*n
и a*0
.
Примеры: 1) a=0, b=L >0
x=![]()
![]()
![]()
![]()
a= - L, b= L
x=![]()
