
- •Матрицы. Определители. Основные понятия.
- •Обратная матрица. Ранг матрицы.
- •Алгоритм нахождения ранга матрицы.
- •Системы линейных уравнений. Системы линейных неравенств.
- •Векторы. N – мерное линейное векторное пространство.
- •Скалярное, векторное, смешанное произведение векторов.
- •Квадратичные формы.
- •7.Кривые второго порядка на плоскости (окружность, эллипс).
- •Пусть и - фокусы эллипса. Начало системы координат расположим на середине отрезка . Ось направим вдоль этого отрезка, ось - перпендикулярно к этому отрезку (рис. 7.2).
- •8. Кривые второго порядка на плоскости (гипербола, парабола).
- •Комплексные числа. Алгебраическая форма записи.
- •10. Геометрическое изображение комплексных чисел. Тригонометрическая форма записи.
- •Многочлены и действия над ними.
- •Функции. Графики основных элементарных функций.
- •Способы задания функции.
- •Графики элементарных функций.
- •Линейная функция.
- •Квадратичная функция
- •Гипербола
- •Степенная функция с натуральным показателнм.
- •Функция .
- •Показательная функция
- •Логарифмическая функция
- •Предел функции.
- •Непрерывность в точке. Виды разрывов.
- •Производная, ее геометрический и физический смысл.
- •Дифференциал, его геометрический и механический смысл.
- •Теоремы о дифференцируемых функциях и их применение.
- •Выпуклость графика функции. Точки перегиба.
- •Первообразная функции. Неопределенный интеграл.
- •Понятие определенного интеграла. Геометрический смысл.
- •Комбинаторика. Понятие множества. Перестановки. Размещения. Сочетания.
- •Формула включений-исключений и ее применения к комбинаторике и теории чисел. Бином Ньютона.
- •Рекуррентные уравнения.
- •Производящие функции.
- •Булевые функции и их представление. Двоичная запись целых чисел.
- •Алгоритм перевода чисел из десятичной системы счисления в двоичную.
- •Перевод чисел из двоичной системы в десятичную.
- •Теория графов. Основные понятия теории графов.
- •Сущность и условия применимости теории вероятностей. Вероятностное пространство.
- •Действия со случайными событиями.
- •Вероятность события. Аксиоматическое определение вероятности.
- •Вероятность события. Классическое определение вероятности.
- •Случайные величины и способы их описания.
- •Модели законов распределения вероятностей, наиболее употребляемые в социально-экономических приложениях.
- •Цепи Маркова и их использование в моделировании социально-экономических процессов.
- •Задача линейного программирования в общем виде.
- •Виды злп и способы перехода от одного вида к другому.
- •Основные теоремы линейного программирования.
- •Симплекс-метод.
- •Метод искусственного базиса.
- •Алгоритм метода искусственного базиса.
- •Двойственность задач линейного программирования. Таблица соответствий.
- •Теоремы двойственности.
- •Критерии оптимальности.
- •Транспортная задача. Закрытая и открытая модели.
- •Теорема о существовании оптимального решения.
- •Целочисленные злп, графический метод решения в случае двух переменных.
- •Задачи о назначениях и о коммивояжере как частные случаи целочисленных злп.
- •Метод ветвей и границ.
- •Алгоритм метода ветвей и границ:
- •Стандартная задача нелинейного программирования.
- •Локальный экстремум. Необходимое и достаточное условия.
- •Глобальный и условный экстремумы
- •Множители Лагранжа.
- •Задача о потребительском выборе.
- •Выпуклые множества, выпуклые и вогнутые функции. Теорема Куна-Таккера.
- •Динамическое программирование. Общая постановка задачи.
- •Функции Беллмана. Уравнения Беллмана. Условно-оптимальные управления.
- •Условная оптимизация.
- •Безусловная оптимизация.
- •Принцип Беллмана для оптимальных путей.
- •I этап. Условная оптимизация.
- •II этап. Безусловная оптимизация.
- •Оптимальное распределение инвестиций как задача динамического программирования.
- •Теория игр. Игровые модели.
- •Платежная матрица. Нижняя и верхняя цена игры. Принцип минимакса.
- •Чистые стратегии. Седловая точка.
- •Решение игр в смешанных стратегиях.
- •Приведение матричной игры к задаче линейного программирования.
- •Биматричные игры. Равновесие Нэша. Оптимальность Парето.
- •60. Игра двух лиц, в которой одним из игроков является "природа"
Функции. Графики основных элементарных функций.
Пусть задано
числовое множество ![]() .
.
Если каждому числу
![]() поставлено в соответствие единственное
число
поставлено в соответствие единственное
число ![]() ,
то говорят, что на множестве
,
то говорят, что на множестве ![]() задана
числовая функция:
задана
числовая функция:
![]()
Множество ![]() называется областью
определения
функции и обозначается
называется областью
определения
функции и обозначается ![]() .
.
Множество, состоящее
из всех элементов ![]() ,
где
называется
областью значений
функции и обозначается
,
где
называется
областью значений
функции и обозначается ![]() .
.
Число ![]() часто называют аргументом
функции или независимой переменной, а
число
– зависимой переменной или, собственно,
функцией переменной
.
Число
часто называют аргументом
функции или независимой переменной, а
число
– зависимой переменной или, собственно,
функцией переменной
.
Число ![]() ,
соответствующее значению
,
соответствующее значению ![]() ,
называют значением
функции в
точке
,
называют значением
функции в
точке ![]() и обозначают
и обозначают ![]() .
.
Для того чтобы
задать
функцию ![]() ,
нужно указать:
,
нужно указать:
1) ее область определения ;
2) указать
правило![]() ,
по которому каждому значению
ставится в соответствие некоторое
значение
,
по которому каждому значению
ставится в соответствие некоторое
значение ![]() .
.
Область определения иногда еще называют областью допустимых значений функции (ОДЗ). Для нахождения ОДЗ функции нужно проанализировать данное соответствие и установить встречающиеся запретные операции (деление на нуль, возведение в рациональную степень отрицательного числа, логарифмические операции над отрицательными числами и т. п.).
Функции
и ![]() называются равными,
если они имеют одну и ту же область
определения D
и для каждого
значения этих функций совпадают. В этом
случае пишут
называются равными,
если они имеют одну и ту же область
определения D
и для каждого
значения этих функций совпадают. В этом
случае пишут ![]() ,
или
,
или ![]() .
.
Если же значения
этих функций совпадают лишь на некотором
множестве ![]() и
и ![]() ,
то говорят,
что функции равны на множестве
,
то говорят,
что функции равны на множестве ![]() .
.
Пусть функции
и ![]() определены на одном и том же множестве
.
Тогда функция, значения которой в каждой
точке
равны
определены на одном и том же множестве
.
Тогда функция, значения которой в каждой
точке
равны ![]() ,
называется суммой
функций
и
и обозначается
,
называется суммой
функций
и
и обозначается ![]() .
Точно так же определяются разность
.
Точно так же определяются разность ![]() ,
произведение
,
произведение ![]() и частное
и частное ![]() двух функций (частное определено на
множестве
,
если на этом множестве
двух функций (частное определено на
множестве
,
если на этом множестве ![]() ).
).
Пусть функции ![]() и
и ![]() определены на множествах
и
определены на множествах
и ![]() соответственно, причем множество
значений функции
содержится в области определения функции
.
Тогда функция, принимающая при каждом
значение
соответственно, причем множество
значений функции
содержится в области определения функции
.
Тогда функция, принимающая при каждом
значение ![]() ,
называется сложной
функций или
суперпозицией
функций
и
и обозначается
,
называется сложной
функций или
суперпозицией
функций
и
и обозначается ![]() .
Важно отметить, что в общем случае
суперпозиция
.
Важно отметить, что в общем случае
суперпозиция ![]() не совпадает с
не совпадает с ![]() .
.
Способы задания функции.
Функции могут задаваться различными способами:
Самый распространенный из них – аналитический, когда числовая функция задается при помощи формулы. Например:
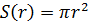 .
.Функция может быть задана различными формулами на разных промежутках. Например:
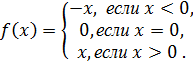
Функции могут задаваться при помощи графиков.
Определение.
Графиком
функции
в выбранной системе координат называется
множество всех точек ![]() ,
для которых выполняется равенство
.
,
для которых выполняется равенство
.
Число ![]() называется нулем функции
,
если
называется нулем функции
,
если ![]() .
.
Графики элементарных функций.
Линейная функция.
Функция ![]() называется линейной функцией.
называется линейной функцией.
График линейной функции является прямой.
Свойства линейной функции:
1).
Область
определения функции: ![]() .
.
2). Область значений:
![]() .
.
3). Линейная функция не является ни четной, ни нечетной.
П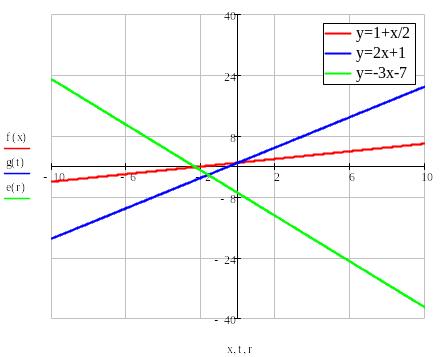 римеры
линейных функций:
римеры
линейных функций:
|
