10. Геометрическое изображение комплексных чисел. Тригонометрическая форма записи.
При изучении свойств комплексных чисел весьма удобной является их геометрическая интерпретация. Поскольку комплексное число определяется как пара действительных чисел, то каждое комплексное число z = a + bi изображается точкой плоскости (x, y) с координатами x = a и y = b. Такая плоскость называется комплексной плоскостью, ось абсцисс ‑ действительной (Re z), а ось ординат ‑ мнимой осью (Im z).
Пример 10.1.
Изобразить
на плоскости точки, соответствующие
числам:
Решение
Р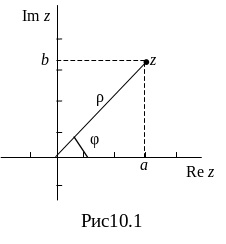
ассмотрим
тригонометрическую форму представления
комплексных чисел
,
где
– модуль комплексного числа, а
– его аргумент.
Связь между
алгебраической и тригонометрической
формами записи можно получить из
равенства:
.
Тогда
,
откуда
.
Возведя оба
равенства в квадрат и сложив их, получим
.
А угол
определяется с точностью до
,
из системы:
(10.1)
Для однозначного
соответствия между комплексным числом
и его аргументом выделим его главное
значение arg
z
, для которого
принимаем:
.
В дальнейшем будем придерживаться
ограничений:
.
Для числа z
= 0 аргумент
не определяется.
Геометрический
смысл
и arg
z
ясен из рис.
10.1:
есть расстояние от точки до начала
координат, а arg
z
– угол, на
который необходимо повернуть вещественную
ось Re
z
до совпадения
с числом z.
Пример 10.2. Представить в тригонометрической форме число z = 1.
Решение.
Многочлены и действия над ними.
Определение.
Для действительной переменной x
функция вида
,
где a
и x
–действительные
числа, а n
– натуральное
число или 0 (по-другому это можно записать
как
),
называется одночленом
с действительным коэффициентом.
Определение. Многочлен ‑ это сумма одночленов, т.е. функция вида
.
При
этом
называется
старшим коэффициентом и
,
‑ свободным членом, n
‑ степенью
многочлена.
Многочлен тождественно равен 0 тогда и только тогда, когда все его коэффициенты равны 0.
Если в записи многочлена нет какой-либо степени неизвестного, это значит, что коэффициент при этой степени равен 0.
На множестве многочленов определены следующие действия:
1. Сложение.
2. Умножение.
3. Деление с остатком.
Разделить
на
‑ значит записать
в виде
,
или
.
Последняя запись аналогична записи для
чисел:
,
или 17 = 5
3 + 2.
Теорема (о
делении с остатком)
[Для любых
многочленов
и
существуют, и притом единственные,
многочлены
и
,
такие, что
. (11.1)
При
этом степень
меньше степени
,
‑ неполное частное,
‑ остаток.
Разделить
на
‑ значит записать
в виде (11.1).
Для практического нахождения частного и остатка существует метод деления «уголком».
Пример 11.1. Выполнить «уголком» деление с остатком:
=
на
=
.
Решение.
Определение.
Корнем
многочлена
называется число
такое что
.
Теорема Безу.
Для любой
функции
и числа
верно равенство:
где
.
Следствие.
Число
является корнем тогда и только тогда,
когда
делится на
без остатка.
Удобной для деления
на многочлены вида (
)
является схема Горнера. Рисуем таблицу,
в первой строке которой записываем все
коэффициенты
(включая нулевые).
|
|
|
|
… |
|
|
|
|
|
|
… |
|
|
‑ коэффициенты
неполного частного от деления
на (
);
‑ остаток от деления, который по
теореме Безу равен
.
Если
=
0, то говорят, что
делится на (
)
нацело и
‑
корень многочлена
.
Пример 11.2.
Разделить
на
.
Решение. Воспользуемся схемой Горнера. Нарисуем таблицу и выполним расчеты.