17. Модели законов распределения вероятностей, наиболее употребляемые в социально-экономических приложениях.

Случайная величина непрерывного типа называется распределенной равномерно на отрезке , если ее плотность распределения постоянна на этом отрезке и равна нулю вне отрезка.

Для равномерно распределенной случайной величины

при . (29.1)

Равномерное распределение используется при решении практических задач, в которых заранее известно, что возможные значения случайной величины лежат в некотором интервале, и все значения в пределах этого интервала одинаково вероятны.

Для случайной величины, распределенной равномерно на отрезке , математическое ожидание и дисперсия вычисляются по формулам: , .

Непрерывная случайная величина ξ называется распределенной по показательному (экспоненциальному) закону, если ее плотность распределения задается формулой:

при и при , (29.2)

где - постоянная положительная величина, которая называется параметром распределения.

Показательное распределение часто встречается в теории массового обслуживания и в теории надежности. Величина ξ, распределенная по показательному закону, хорошо описывает время ожидания при техническом обслуживании и длительность телефонных разговоров, регистрируемых на телефонной станции, и срок службы радиоэлектронной или другой аппаратуры.

Для случайной величины, распределенной по показательному закону с параметром , математическое ожидание и дисперсия вычисляются по формулам: , . Среднее квадратическое отклонение - .

Случайная величина ξ называется распределенной по нормальному (гауссовскому) закону с параметрами а и ( ), если плотность распределения вероятностей имеет вид

, (29.3)

где .

Теоретические исследования показали, что большинство встречающихся на практике случайных величин имеет нормальный закон распределения. По этому закону распределяется скорость газовых молекул, вес новорожденных, размер одежды и обуви населения страны и много других случайных событий физической и биологической природы. Впервые эту закономерность заметил и теоретически обосновал А. Муавр.

Величина, распределенная по нормальному закону, всегда имеет бесчисленное множество возможных значений, поэтому ее удобно изображать графически. Вероятность того, что случайная величина примет значение из интервала , равна площади под графиком функции на этом интервале (геометрический смысл определенного интеграла).

На рисунке 29.1 изображено несколько кривых плотности распределения случайной величины, заданной по нормальному закону. Несмотря на все различия, эти кривые обладают следующими общими чертами.

1. Все кривые имеют одну точку максимума, при удалении от которой вправо и влево кривые убывают. Максимум достигается при и равен .

2. Кривые симметричны относительно вертикальной прямой, проведенной через наивысшую точку.

3. Площадь подграфика каждой кривой равна 1. Это следует из свойства

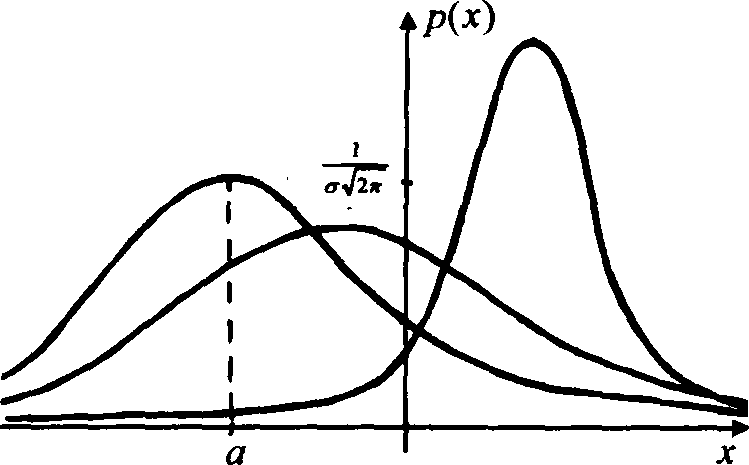
Рис. 29.1.

Для случайной величины, распределенной по нормальному закону с параметрами а и , математическое ожидание и дисперсия вычисляются по формулам: , . Среднее квадратическое отклонение равно .

Вероятность того, что нормально распределенная величина примет значение из интервала , равна

, (29.4)

где есть функция Лапласа.

Часто в задачах требуется вычислить вероятность того, что отклонение нормально распределенной случайной величины ξ от своего математического ожидания по абсолютной величине не превосходит некоторого значения , т.е. вычислить вероятность .

Применяя формулу (29.4), имеем:

. (29.5)

В заключение приведем одно важное следствие из формулы (29.5). Положим в этой формуле . Тогда , т.е. вероятность того, что абсолютная величина отклонения ξ от своего математического ожидания не превысит , равна 99,73%. Практически такое событие можно считать достоверным. В этом и состоит сущность правила трех сигм: если случайная величина распределена нормально, то абсолютная величина ее отклонения от математического ожидания практически не превосходит утроенного среднего квадратического отклонения.