17. Понятие определенного интеграла. Геометрический смысл.

Пусть функция определена на отрезке . Разобьем и отрезок точками на n частей .

Определение. Интегральной суммой функции на отрезке называется сумма вида , где , .

Если , то геометрически представляет собой сумму площадей прямоугольников, имеющих основания и высоты .

Определение. Если функция такова, что существует конечный предел интегральных сумм при условии, что ранг разбиения , , стремится к нулю, причем этот предел не зависит ни от способа разбиения отрезка на отрезки , ни от выбора точек на этих отрезках, то функция называется интегрируемой на отрезке , а сам предел называется определенным интегралом от функции на отрезке и обозначается . Таким образом,

= (20.1)

Отметим, что непрерывная на отрезке функция интегрируема на этом отрезке.

Основные свойства определенного интеграла.

Пусть функции и интегрируемы на . Тогда выполнено:

1) = ,

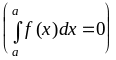2. Аддитивность: = 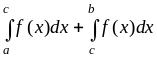для

2. Линейность: ,

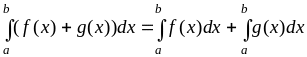для любой константы .

2. Интегрирование неравенств:

Если функции интегрируемы на отрезке и для верно неравенство , то .

5. Функция 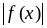интегрируема на и ,

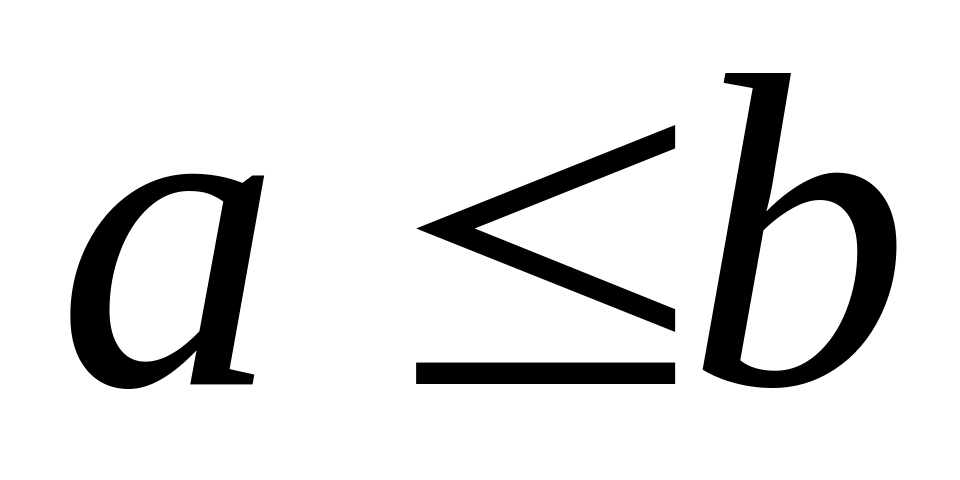
6. Формула Ньютона-Лейбница. Если функция непрерывна на , то для любой ее первообразной имеет место формула:

= .

Формулы замены переменной и интегрирования по частям для определенного интеграла схожи с аналогичными формулами для неопределенного интеграла.

17. Комбинаторика. Понятие множества. Перестановки. Размещения. Сочетания.

Часто приходится иметь дело с задачами, в которых нужно подсчитать число всех возможных способов расположения некоторых предметов или число всех возможных способов осуществления некоторого действия. Разные пути или варианты, которые приходится выбирать, складываются в самые разнообразные комбинации. Целый раздел математики, называемый комбинаторикой, занят поиском ответов на вопросы: сколько всего есть комбинаций в том или другом случае.

Определение. Число различных способов, которыми может быть упорядочено данное множество, состоящее из элементов, называется числом перестановок множества и обозначается . Число перестановок из элементов вычисляется следующим образом:

(21.1.)

Определение. Количество перестановок из элементов, среди которых имеется одинаковых элементов первого сорта, одинаковых элементов второго сорта, одинаковых элементов k-го сорта, называется количеством перестановок с повторениями, обозначается символом . Число перестановок с повторениями вычисляется по формуле

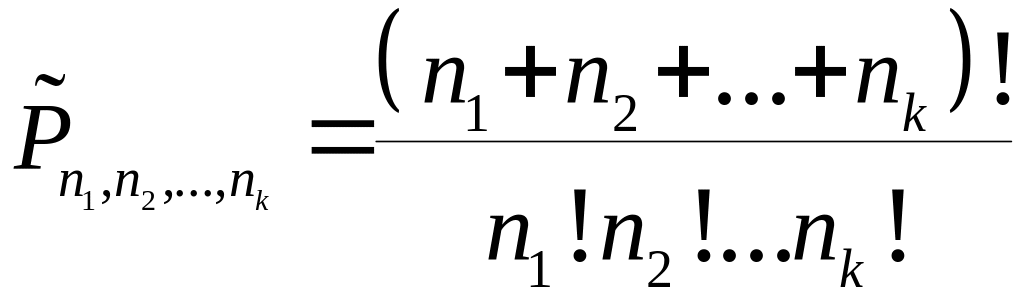(21.2)

Пусть задано некоторое конечное множество из различных элементов. Пусть из числа его элементов выбраны различных штук ( ), тогда говорят, что произведена выборка объёма . Если важен порядок, в котором произведена выборка элементов, то говорят об упорядоченной выборке, если порядок не важен, то о неупорядоченной выборке.

Определение.  Упорядоченная выборка объёма из множества, состоящего из элементов, ( ) называется размещением из элементов по и обозначается .

Количество размещений из элементов по вычисляется следующим образом:

(21.3)

Познакомившись с размещением вернемся к понятию перестановки.

Определение.  Размещение из элементов по называется перестановкой из элементов и обозначается .

Другими словами,

Определение.  Упорядоченная выборка объёма из множества, состоящего из элементов называется размещением с повторением из элементов по и обозначаются .

Количество размещений с повторениями вычисляется по формуле

(21.4)

Допустим теперь, что нас не интересует порядок, в котором идут выбранные элементы. Например, нужно из десяти человек выбрать троих дежурных. Такая операция называется неупорядоченной выборкой, или сочетанием, в отличие от упорядоченной выборки – размещения.

Определение.  Всякая неупорядоченная выборка объёма из множества, состоящего из элементов, ( ) называется сочетанием из элементов по и обозначается .

Количество сочетаний из элементов по вычисляется по формуле

(21.5)

Как и в случае с размещениями, существует понятие числа сочетаний с повторениями.

Определение. Если из множества, содержащего n элементов, выбирается поочередно m элементов, причём выбранный элемент каждый раз возвращается обратно, то количество способов произвести неупорядоченную выборку называется сочетанием с повторениями и обозначается .

Количество способов произвести неупорядоченную выборку – число сочетаний с повторениями составляет

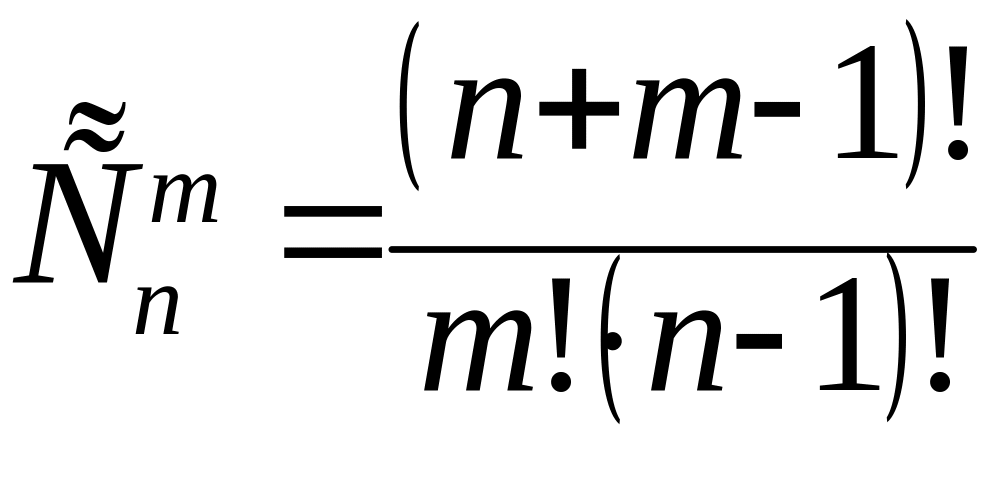(21.6)