Непрерывность в точке. Виды разрывов.
Определение.
Функция
называется непрерывной
в точке
,
если существует предел функции в этой
точке и он равен значению функции в этой
точке, т. е.
.
В определении
предела функции при
считается, что
стремится к
любым способом: справа (оставаясь
больше
),
слева (оставаясь меньше
)
или колеблясь около точки
.
Часто способ приближения
к
влияет на значение предела функции,
поэтому вводят понятие односторонних
пределов.
Определение.
Пусть функция
определена
на некотором полуинтервале
,
для которого
-
левый конец. Функция
называется
непрерывной
справа в точке
,
если существует предел
при
и этот
предел равен значению
,
то есть
Определение.
Пусть функция
определена
на некотором полуинтервале
,
для которого
--
правый конец. Функция
называется
непрерывной
слева в точке
,
если существует предел
при
и
этот предел равен значению
,
то есть
Определение. Функция тогда и только тогда непрерывна в точке , когда она непрерывна в точке справа и слева, то есть когда выполнены следующие условия:
1) функция определена в точке и в некоторой окрестности этой точки;
2) существует предел
значений функции слева:
;
3) существует предел
значений функции справа:
;
4) эти два предела
совпадают между собой и со значением
функции в точке
:
.
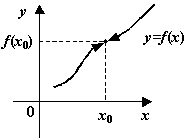
Рис.14.1.Функция непрерывна: пределы слева и справа совпадают с .
Дадим теперь определение точек разрыва функции.
Определение. Точка называется точкой разрыва функции , если она определена в некоторой проколотой окрестности точки (то есть определена на некотором интервале, для которого служит внутренней точкой, но в самой точке , возможно, не определена) и выполняется хотя бы одно из следующих условий:
1) не существует
предела слева
;
2) не существует
предела справа
;
3) пределы слева
и справа
существуют,
но не равны друг другу:
;
4) пределы слева
и справа
существуют
и равны друг другу:
,
но не совпадают со значением функции в
точке
:
,
или функция
не определена
в точке
.
Если имеет место либо случай 3, либо случай 4, то точка разрыва называется точкой разрыва первого рода, а поведение функции в окрестности точки называется разрывом первого рода в точке ; в случае 4 точка разрыва первого рода называется устранимой точкой разрыва, а разрыв функции в этой точке - устранимым разрывом.
Если же имеет место либо случай 1, либо случай 2 (либо и тот и другой сразу), то точка разрыва называется точкой разрыва второго рода, а поведение функции в окрестности этой точки - разрывом второго рода в точке .
Итак, если функция
имеет
разрыв первого рода в точке
,
то существуют, как часто говорят, значения
функции "на берегах разрыва":
и
,
но точка
не
является точкой непрерывности.
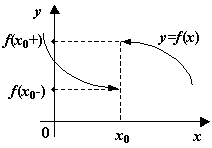
Рис.14.2. -точка разрыва первого рода
Если значения на
берегах разрыва разные, то значение
функции в точке
может быть
любым (или вообще отсутствовать), всё
равно
будет
давать разрыв первого рода. Если же
значения на берегах разрыва совпадают,
то для наличия разрыва нужно, чтобы либо
эти совпадающие значения были отличны
от значения функции в точке
,
либо функция в этой точке была вовсе не
определена. Если в этом случае
переопределить (или доопределить)
функцию
в
точке
,
положив
,
то полученная изменённая функция будет
уже непрерывна в точке
и
разрыв в точке
исчезнет;
отсюда и название такого разрыва -
устранимый.
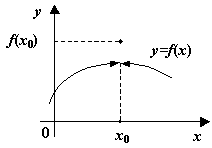
Рис.14.3. - точка устранимого разрыва
Наконец, к разрывам второго рода, как видно из определения, относятся все разрывы, которые не принадлежат к разрывам первого рода; некоторые из возможных способов поведения функции в окрестности точки , где происходит разрыв второго рода, представлены на следующем рисунке.
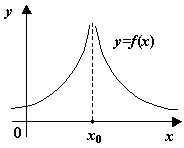
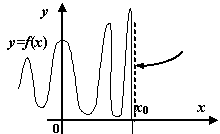
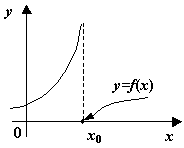
Рис.14.4. -- точка разрыва второго рода. Некоторые возможные варианты
Замечание. Если функция не определена на интервале, примыкающем к точке слева или справа, то точку мы не считаем точкой разрыва функции.