12. Постулаты специальной теории относительности Эйнштейна. Преобразования Лоренца и следствия из них.

Постулаты специальной теории относительности Эйнштейна:

1. Никакие опыты (механические, электрические, оптические), проведенные внутри данной инерциальной системы отсчета, не дают возможности обнаружить, покоится ли эта система или движется равномерно и прямолинейно, т.е. все законы природы инвариантны по отношению к переходу от одной инерциальной системы отсчета к другой.

2. Скорость света в вакууме не зависит от скорости движения источника света или наблюдателя и одинакова во всех инерциальных системах отсчета.

13.Масса, импульс и основной закон динамики в релятивистской механике. Кинетическая энергия в релятивистской механике. Границы применимости классической механики.

14. Неинерциальные системы отсчета. Силы инерции.

Законы Ньютона выполняются только в инерциальных системах отсчета. Системы отсчета, движущиеся относительно инерциальных систем с ускорением, называются неинерциальными. В неинерциальных системах законы Ньютона несправедливы. Однако законы динамики можно использовать и для неинерциальных систем, если, кроме сил F, обусловленных воздействием тел друг на друга, ввести в рассмотрение силы инерции F_ин. Если учесть силы инерции, то второй закон Ньютона будет справедлив для любой системы отсчета: произведение массы тела на ускорение в рассматриваемой системе отсчета равно сумме всех сил, действующих на данное тело (включая и силы инерции).

Существенно, что силы инерции вызываются не взаимодействием тел, а ускоренным движением системы отсчета . Поэтому эти силы не подчиняются третьему закону Ньютона, так как если на какое-либо тело действует сила инерции, то не существует противодействующей силы, приложенной к данному телу.

15. Колебательное движение. Гармоническое колебание и его характеристики. Скорость и ускорение при гармонических колебаниях.

Колебаниями называются движения или процессы, которые характеризуются определенной повторяемостью во времени. Колебательное движение характеризуется амплитудой, т. е. максимальным смещением от положения равновесия.

Период Т — минимальный промежуток времени, через который движение тела полностью повторяется, или промежуток, в течение которого происходит полное колебание (Т=1/ν). Величина, обратная периоду, — частота, т. е. число колебаний в секунду (ν=1/Т).

Гармоническими колебаниями называются колебания, при которых изменения физических величин происходят по закону косинуса или синуса (гармоническому закону): 1) колебания, встречающиеся в природе и технике, часто имеют характер, близкий к гармоническому; 2) различные периодические процессы (повторяющиеся через равные промежутки времени) можно представить как наложение гармонических колебаний.

Свободные колебания – если они совершаются за счет первоначально накопленной энергии при последующем отсутствии периодических внешних воздействий, сил трения, торможения.

, где ω – частота колебания (ω=2π/Т=2πn), xm – амплитуда колебания, φ0 и φ0’ – начальные фазы колебания.

Выражение, стоящее под знаком cos или sin, наз. фазой колебания: .

Фаза колебания измеряется в радианах и определяет значение смещения (колеблющейся величины) в данный момент времени.

Амплитуда колебания зависит только от начального отклонения (начальной энергии, сообщенной колебательной системе).

Согласно определению скорости, скорость – это производная от координаты по времени.

Величина - максимальная скорость колебательного движения (амплитуда колебаний скорости).

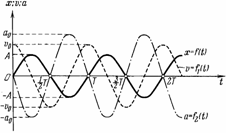С огласно определению ускорения, ускорение – это производная от скорости по времени или вторая производная от координаты по времени. Тогда:

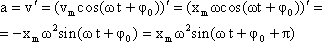
Ускорение при гармоническом колебательном движении также изменяется по гармоническому закону, но колебания ускорения опережают колебания скорости на p/2 и колебания смещения на p (говорят, что колебания происходят в противофазе).

Из анализа процесса колебательного движения, графиков и соответствующих математических выражений видно, что при прохождении колеблющимся телом положения равновесия (смещение равно нулю) ускорение равно нулю, а скорость тела максимальна (тело проходит положение равновесия по инерции), а при достижении амплитудного значения смещения – скорость равна нулю, а ускорение максимально по модулю (тело меняет направление своего движения).