Правило нахождения присоединенных векторов

ОбозначимА матрицу линейного оператора в некотором базисе, – координатный столбец вектора 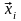в том же базисе. Тогда в матричном виде уравнение для нахождения будет выглядеть так:

что равносильно уравнению

.

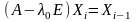Таким образом, видим, что для отыскания i-го присоединенного вектора к собственному вектору с собственным значением 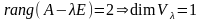следует решить систему линейных уравнений с той же матрицей, что и для отыскания собственного вектора , но неоднородную, причем в качестве столбца свободных членов берется координатный столбец предыдущего присоединенного вектора.

54. Определение приводимости квадратной матрицы к диагональному виду и вторая теорема о приводимости. Следствие.

Определение. Говорят, что квадратная матрицаА с элементами из поля P приводится к диагональному виду над P, если существует невырожденная квадратная матрица Т с элементами из P такая, что матрица – диагональная.

Теорема 4.14. Для того чтобы квадратная матрица А n-го порядка приводилась к диагональному виду над полем Р, необходимо и достаточно, чтобы все ее характеристические числа принадлежали этому полю и для каждого из них выполнялось условие

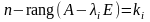, (4.58)

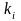где – кратность корня характеристического уравнения матрицы А.

60.Канонический вид квадратичной формы

Мы уже говорили о том, что в каждом базисе линейного пространства квадратичная форма задается однородным многочленом второй степени, который называется видом данной квадратичной формы.

Каноническим видом квадратичной формы называется такой ее вид, в котором коэффициенты при произведениях разноименных переменных равны 0, т. е. при .

Нормальным видом действительной квадратичной формы называется такой ее канонический вид, в котором отличные от нуля коэффициенты при квадратах равны 1 или –1. Все отличные от нуля коэффициенты при квадратах нормального вида комплексной квадратичной формы равны 1.

Теорема 5.6. Для любой квадратичной формы, заданной на линейном пространстве в существует базис, в котором эта квадратичная форма имеет канонический вид, и существует базис, в котором она имеет нормальный вид.

61.Знакоопределенные квадратичные формы

Определения. Квадратичная форма называется положительно определенной, если она принимает положительные значения для любого нетривиального набора переменных.

Квадратичная форма называется отрицательно определенной, если она принимает отрицательные значения для любого нетривиального набора переменных.

Квадратичная форма называется положительно (отрицательно) полуопределенной, если для любого нетривиального набора переменных она принимает либо положительное (отрицательное) значение, либо 0.

Квадратичная форма знаконеопределена, если существует нетривиальный набор переменных, при которых она принимает положительное значение, и существует нетривиальный набор переменных, при которых она принимает отрицательное значение.

Лемма 5.4 (необходимое условие знакоопределенности). Если квадратичная форма положительно (отрицательно) определена, то все ее коэффициенты при квадратах положительны (отрицательны).