38. Определение линейного оператора и его простейшие свойства.

Определение. Пусть и – линейные пространства над одним и тем же полем . Отображение называется линейным оператором, если оно удовлетворяет следующим условиям:

1*.

2*.

Следствие. При линейном операторе образ линейной комбинации векторов равен такой же линейной комбинации их образов, т. е. если – линейный оператор, то :

(4.3)

1º. Линейный оператор переводит нейтральный элемент пространства в нейтральный элемент пространства .

2º. При линейном операторе линейно зависимые векторы пространства переходят в линейно зависимые векторы пространства

39. Определение матрицы линейного оператора.

Пусть в линейном пространстве над полем задан базис

(4.8)

и пусть – линейный оператор (читается так: в себя). Построим систему векторов

( ). (4.9)

Каждый из векторов системы (4.9) можно разложить по базису (4.8):

(4.10)

Сокращенно система (4.10) записывается одним равенством:

. (4.11)

Расположим числа в матрицуА по нашей договоренности: верхний индекс обозначает номер строки, а нижний – номер столбца:

Заметим, что столбцы полученной матрицыА являются координатными столбцами образов векторов базиса (4.8) в том же базисе. Обозначим

[ ] = .

Равенство (4.11) можно переписать и так: , откуда, руководствуясь правилом цепочки, (4.11) записываем в матричном виде:

. (4.12)

Матрицей линейного оператора в некотором базисе называется матрицаА, столбцами которой являются координатные столбцы образов базисных векторов в том же базисе. Это матрица , элементы которой удовлетворяют системе равенств (4.10) или (4.11), а сама матрица удовлетворяет матричному равенству (4.12).

42.Операции над линейными операторами

Определения. Пусть 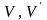и – линейные пространства над одним и тем же полем .

Суммой линейных операторов и называется отображение такое, что : .

Произведением линейного оператора на число называется отображение такое, что : .

Произведением линейных операторов и называется отображение такое, что : 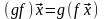(т. е. произведение линейных операторов – это просто произведение или композиция отображений).

Теорема 4.3. Сумма линейных операторов, произведение линейного оператора на число и произведение линейных операторов также являются линейными операторами. При этом, если , А и В – матрицы линейных операторов f и g соответственно в некотором базисе пространства , то матрицы операторов , и gf в том же базисе совпадают соответственно с матрицами А + В, αА и ВА.