15.Ранг матрицы

Определение. Рангом матрицы называется наивысший порядок отличных от нуля ее миноров. Ранг нулевой матрицы по определению равен нулю. Ранг матрицы будем обозначать так: .

Замечание. Если все миноры k-го порядка матрицы А равны нулю, то все ее миноры (k + 1)-го порядка тоже равны нулю. Таким образом, если , это значит, что у матрицы А есть отличный от нуля минор r-го порядка, а все ее миноры (r + 1)-го порядка равны нулю.

Определение. Элементарными преобразованиями матрицы называются:

1) умножение строк и столбцов на число, отличное от 0;

2) прибавление к какой либо строке (столбцу) другой строки (столбца), умноженной на число;

3) перестановка строк или столбцов.

Теорема 2.2. Элементарные преобразования не меняют ранга матрицы.

Свойства ранга матрицы

1°. Ранг матрицы не превосходит ни количества ее строк, ни количества столбцов.

2°. При транспонировании матрицы ее ранг не меняется.

3°. Если rang A = 0, то A – нулевая матрица.

4°. Если у матрицы вычеркнуть столбец или строку, полностью состоящую из нулей, то ее ранг при этом не изменится.

5°. Если у матрицы вычеркнуть одну из двух пропорциональных строк (столбцов), то ее ранг при этом не изменится.

6°. Ранг произведения матриц не превосходит ранга каждого из сомножителей. При этом если один из сомножителей – невырожденная матрица, то ранг произведения равен рангу второго сомножителя.

Первые четыре свойства очевидны, пятое вытекает из доказанной теоремы, а шестое мы докажем позже, в четвертой главе.

16.Теорема о базисном миноре

Определение. Строки матрицы А

(2.7)

называются линейно зависимыми, если существуют числа , не все равные нулю такие, что

. (2.8)

Строки (2.7) называются линейно независимыми, если равенство (2.8) выполняется только в том случае, когда .

Аналогично формулируется определение линейной зависимости и независимости для столбцов матрицы (позднее мы введем понятия линейной зависимости и независимости в общем случае).

Определение. Базисным минором матрицы называется любой отличный от нуля ее минор, порядок которого равен рангу этой матрицы. Строки (столбцы), проходящие через базисный минор, называются базисными.

18.Критерий совместности системы линейных уравнений

Теорема 2.5 (Кронекера – Капелли или критерий совместности системы линейных уравнений). Для того чтобы система линейных уравнений была совместной, необходимо и достаточно, чтобы ранг матрицы системы равнялся рангу расширенной матрицы .

19.Однородные системы линейных уравнений

Определение. Система линейных уравнений называется однородной, если во всех ее уравнениях свободные члены равны нулю:

Часто удобно использовать и матричную запись:

АХ = О. (2.18)

Однородная система всегда совместна, она имеет, по крайней мере, решение , которое называется тривиальным. Исследуем возможность существования других решений. Предположим, что и что ее базисный минор расположен в левом верхнем углу. Тогда можно отбросить последних линейно зависимых уравнений. Неизвестные, коэффициенты при которых образуют базисный минор, называют базисными неизвестными, а остальные – свободными. Преобразуем систему следующим образом: базисные неизвестные оставим в левой части, а свободные перенесем направо. Получим систему уравнений, равносильную исходной:

(2.19)

Рассмотрим различные случаи.

1. Если , то в системе (2.19) число уравнений равно числу неизвестных, ее определитель совпадает с базисным минором и поэтому отличен от 0. Значит, по правилу Крамера система (2.19) имеет единственное решение, которое является тривиальным.

2. Пусть . Придадим свободным неизвестным какие-либо значения . Подставляя их в (2.19), получаем систему крамеровского типа:

(2.20)

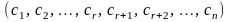Она имеет единственное решение . Тогда упорядоченный набор – решение системы (2.19) и исходной системы. Так как свободным неизвестным можно придать значения бесконечным числом способов, то при условии однородная система линейных уравнений имеет бесконечное множество решений.

Вывод. Для того чтобы однородная система линейных уравнений имела нетривиальные решения, необходимо и достаточно, чтобы ранг ее матрицы был меньше количества неизвестных. В частности, если в однородной системе число уравнений равно числу неизвестных, то для существования нетривиальных решений необходимо и достаточно, чтобы определитель матрицы системы был равен нулю.

.