82.Ортогональные операторы в трехмерном евклидовом пространстве

Известно, что всякий многочлен третьей степени с действительными коэффициентами имеет, по крайней мере, один действительный корень. Поэтому всякий линейный, в том числе и ортогональный оператор 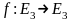имеет, по крайней мере, одно собственное значение , причем 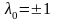. Пусть 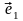– единичный собственный вектор ортогонального оператора с собственным значением . Обозначим 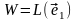и рассмотрим . Очевидно, – двумерное евклидово пространство. Выберем произвольные векторы 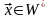и . Тогда

– собственный ортогональность .

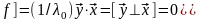
Обозначим такой линейный оператор, что

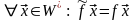
( отличается от только областью определения). Очевидно, – тоже ортогональный оператор. Как и в любом евклидовом пространстве, в пространстве можно выбрать ортонормированный базис . Тогда – ортонормированный базис пространства 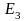. Матрица оператора в этом базисе имеет блочно диагональный вид ,

где – матрица оператора в базисе . В силу того, что оператор ортогональный, матрица тоже ортогональная. Это значит, что в подходящем ортонормированном базисе она может быть одной из матриц:

.

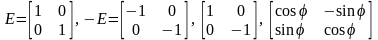Перечисляя всевозможные принципиально различные виды матриц в подходящем ортонормированном базисе пространства , получаем

а) .

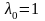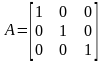, – тождественный оператор;

, – симметрия относительно оси с направлением вектора ;

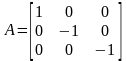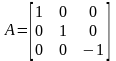, – симметрия относительно плоскости, перпендикулярной вектору ;

, – поворот вокруг оси с направлением вектора .

б) .

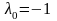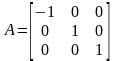, – симметрия относительно плоскости, перпендикулярной вектору ;

, – симметрия относительно начала координат;

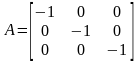, – симметрия относительно оси с направлением вектора ;

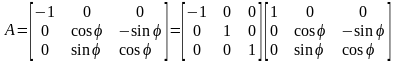, – композиция поворота вокруг оси с направлением вектора и симметрии относительно плоскости, перпендикулярной этому же вектору.

Таким образом, все ортогональные операторы в трехмерном евклидовом пространстве – это: тождественный; симметрия относительно плоскости; симметрия относительно оси; симметрия относительно начала координат; поворот вокруг оси и композиция поворота вокруг оси и симметрии относительно плоскости, перпендикулярной этой же оси.

83.Симметричные операторы в

Как было доказано в § 3, для любого симметричного оператора в существует ортонормированный базис, в котором матрица оператора имеет диагональный вид. Перечислим все принципиально возможные различные случаи.

– тождественный оператор;

– симметрия относительно оси;

– симметрия относительно плоскости;

– симметрия относительно начала координат;

(перечисленные операторы одновременно являются и ортогональными);

– нулевой оператор;

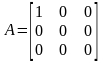– проектирование на ось с направлением вектора ;

– проектирование на плоскость, перпендикулярную вектору ;

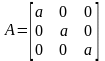– растяжение при и сжатие при ;

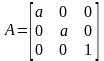– растяжение от оси при и сжатие к оси при ;

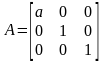– растяжение вдоль оси при и сжатие вдоль оси при

.

Рассмотрим теперь некоторую диагональную матрицу

,

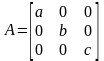в которой, например, 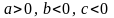. Тогда

,

т. е. оператор, заданный матрицей , есть композиция растяжений (или сжатий) вдоль трех взаимно перпендикулярных осей и симметрии относительно оси. Любая диагональная матрица может быть представлена в виде произведения перечисленных выше десяти простейших матриц. Например, при положительных и

,

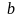
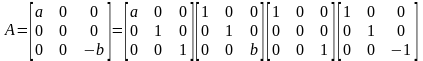откуда вытекает, что оператор с такой матрицей есть композиция двух растяжений вдоль осей, проектирования на плоскость и симметрии относительно другой плоскости.