62.Критерий Сильвестра знакоопределенности квадратичных форм

Теорема 5.9 (критерий Сильвестра). Для того чтобы квадратичная форма была положительно определенной, необходимо и достаточно, чтобы все главные миноры ее матрицы были положительными. Для того чтобы квадратичная форма была отрицательно определенной, необходимо и достаточно, чтобы все главные миноры ее матрицы нечетного порядка были отрицательными, а четного – положительными.

63.Действительные евклидовы пространства

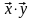Определение. Говорят, что на действительном линейном пространстве задана операция скалярного произведения, если задан закон, по которому каждой паре элементов ставится в соответствие действительное число, которое называется их скалярным произведением, обозначается и удовлетворяет следующим аксиомам:

1*. .

2*. .

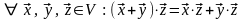3*.

4*. причем .

Простейшие следствия из аксиом

1º.

2º.

3º.

Таким образом, скалярное произведение на действительном линейном пространстве – это положительно определенная симметричная билинейная форма.

Определение. Действительным евклидовым (или просто евклидовым) пространством называется действительное линейное пространство, в котором задана операция скалярного произведения.

63-64.Примеры действительных евклидовых пространств

1. Пространство 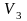свободных векторов с введенным в нем обычным скалярным произведением . Очевидно, всем аксиомам скалярного произведения оно удовлетворяет (эти аксиомы просто «списаны» со свойств обычного скалярного произведения).

2. Пространство , в котором скалярное произведение задается равенством

(см. § 5 гл. 3).

3. Пространство непрерывных на отрезке функций, в котором скалярное произведение задается так:

.

64.Комплексные евклидовы (унитарные) пространства

Определение. Говорят, что на комплексном линейном пространстве задана операция скалярного произведения, если задан закон, по которому каждой паре элементов ставится в соответствие комплексное число, которое называется их скалярным произведением, обозначается и удовлетворяет следующим аксиомам:

1*. .

2*. .

3*.

4*. причем .

простейшие следствия:

1º.

2º.

Примером комплексного евклидова пространства является пространство , в котором скалярное произведение задается равенством

.

65. Неравенство Коши – Буняковского.

В любом евклидовом пространстве модуль скалярного произведения двух векторов не превосходит произведения их длин, т. е.

. (6.1)

Следствие. Для любых ненулевых векторов и евклидова пространства справедливо неравенство

Это позволяет в действительном евклидовом пространстве ввести понятие угла между векторами (в комплексном пространстве понятие угла не вводится).

Определение. Углом между ненулевыми векторами и в действительном евклидовом пространстве называется угол такой, что .

Теорема 6.2 (неравенство треугольника). Длина суммы любых двух векторов евклидова пространства не превосходит суммы их длин, т. е.

.