6 Элементы и параметры электрических цепей переменного тока

Реальные электротехнические устройства обладают электрическим сопротивлением R, индуктивностью L и емкостью C, которые являются параметрами электрической цепи переменного тока. В схемах электрических цепей переменного тока используются комбинации этих параметров при различных способах соединения элементов цепи.

При расчетах, в цепях переменного тока для мгновенных значений можно использовать все законы и правила постоянного тока.

6.1 Цепь с активным сопротивлением

Лампы накаливания, печи сопротивления, бытовые нагревательные приборы (утюги) и другие электроприемники, в которых происходит преобразование электрической энергии в тепловую, обычно представлены только сопротивлением R

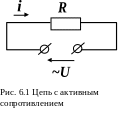Если напряжение u = U_m sin(t + ) подвести к сопротивлению R, то через сопротивление пройдет переменный ток

(6.1)

Следовательно, напряжение на зажимах сопротивления и ток, про­ходящий через это сопротивление, имеют одинаковую начальную фазу, или, как говорят, совпадают по фазе: они одновременно достигают своих амплитудных значений U_m и I_т и, соответственно, одновременно проходят через нуль, см. рис.6.1.

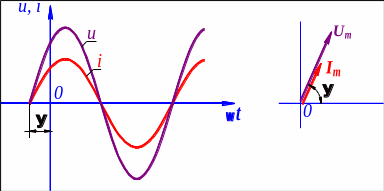
Рис. 6.2 Графики и векторная диаграмма цепи с активным сопротивлением

В данном случае фазовый сдвиг между напряжением и и током i (и соответственно между векторами напряжения и тока ) равен нулю:

 = _u - _I = 0 (6.2)

Другими словами, напряжение и ток совпадают по фазе.

При прохождении переменного тока через сопротивление R не только мгновенные значения напряжения на сопротивлении и тока в нем, но и амплитуды и соответственно действующие значения напряжения и тока связаны законом Ома:

U_m=RI_m; U=RI (6.3)

Мгновенная мощность, поступаю­щая в сопротивление,

р_R=ui=U_mI_m sin²(t+) (6.4)

Вспомним тригонометрию:

(6.5)

С учетом этого и убрав начальную фазу, чтобы она не мешала для дальнейших рассуждений:

(6.6)

П 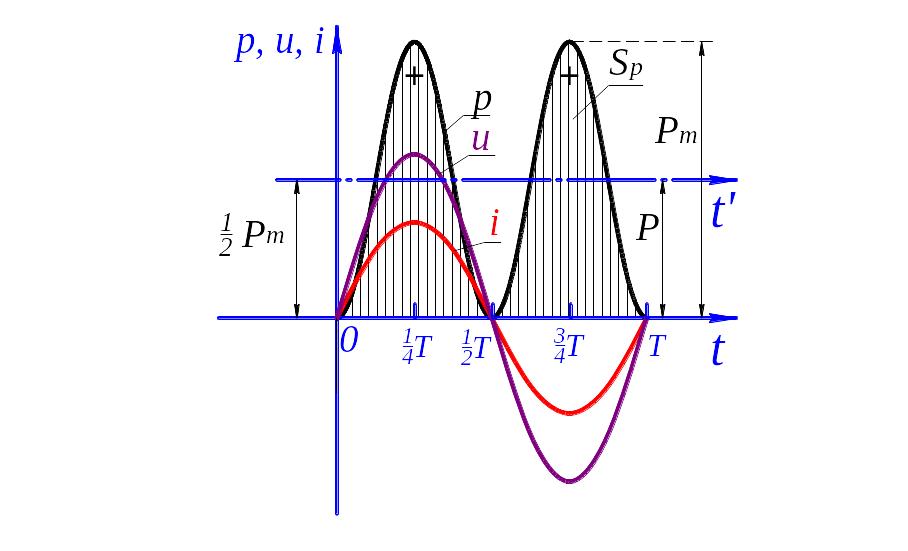опробуем построить график мгновенной мощности. Значения этой величины в любой момент времени будут являться произведениями мгновенного тока на мгновенное напряжение. Если для полученной кривой провести собственную ось времени t', поднятую относительно оси тока и напряжения на величину , то мы увидим, что график мощности является косинусоидальной величиной с двойной частотой.

Рис. 6.3 Мгновенная мощность цепи с

активным сопротивлением

Ввиду того, что в рассматривае­мом случае напряжение и ток сов­падают по фазе, т. е. всегда имеют одинаковый знак (плюс или минус), их произведение всегда положительно – относительно первоначальной оси времени.

Постоянство знака мощности говорит о том, что направление потока электроэнергии остается неизменной, т.е. электроэнергия направлена к приемнику, где необратимо преобразуется в другой вид энергии. Поэтому эта энергия называется активной электрической энергией, а потребляемая мощность – активной мощностью.

Активная мощность равна среднеарифметической мощности за период.

Посмотрим на график еще раз. Средняя величина мощности Р равна высоте прямоугольника с основанием Т , площадь которой равна заштрихованной области на графике. Нетрудно убедиться, что это условие выполняется, если высоту прямоугольника принять равной . Тогда:

(6.7)

Активная мощность цепи с сопротивлением равна произведению действующих величин тока и напряжения.

(6.8)

Сопротив­ление проводника при переменном токе больше, чем при постоянном токе (вследствие явлений поверхно­стного эффекта, эффекта близости, возникновения вихревых токов и из­лучения электромагнитной энергии в пространство). В отличие от сопро­тивления при постоянном токе, ко­торое называют омическим, со­противление проводника при пере­менном токе называется актив­ным сопротивлением. Именно оно и присутствует в последней формуле.

В теории электромагнитного по­ля доказывается, что вследствие по­верхностного эффекта сопротивле­ние r_f провода круглого сечения диаметром d при частоте f связано с сопротивлением того же провода r₀ при постоянном токе формулой: r_f= r₀(1+0,0385d ), т. е. «надбавка» сопротив­ления растет пропорционально кор­ню квадратному из частоты.

Задача. Электрические лампы накаливания, с общей мощностью 900 Вт, включены в сеть переменного тока с напряжением u = 169 sin(314t+60⁰). Определить действующий ток в цепи и написать уравнение тока в сети.

Построить в масштабе графики напряжения и тока в прямоугольной системе координат и векторную диаграмму цепи.