5. Действующая и средняя величины переменного тока

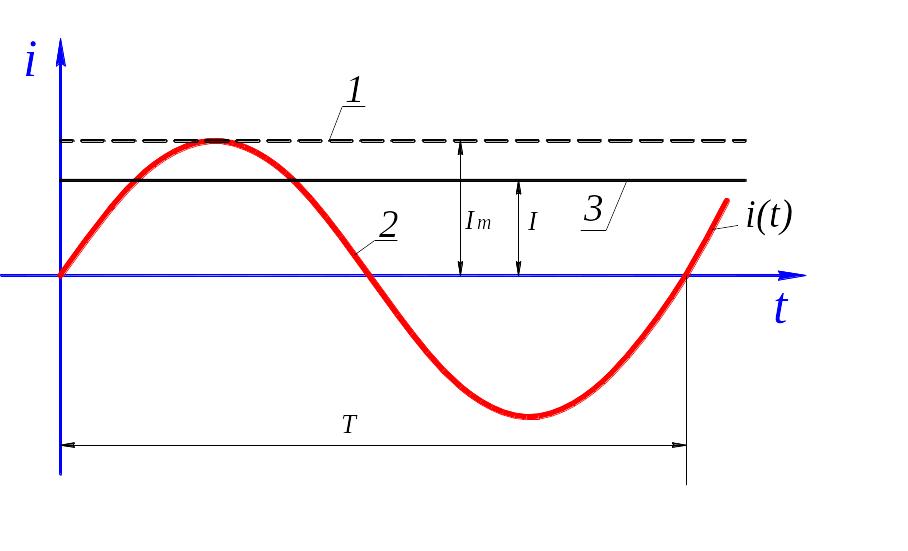
Рис. 5.6 Действующая и средняя величины переменного тока

О переменном токе известно все, если заданы его уравнение или график. Однако на практике пользоваться уравнениями или графиками токов затруднительно.

Переменный ток обычно характеризуется его действующим значением I. Для выпрямительных устройств пользуются средними значениями ЭДС, тока, напряжения.

При определении действующей величины переменного тока принимается во внимание количество теплоты, выделяемой в элементе электрической цепи.

Сравним переменный ток с постоянными токами, см рис. 5.6.

Постоянный ток (1), равный амплитуде переменного (2), в одном и том же элементе выделит больше теплоты. Это связано с тем, что за полупериод переменный ток меньше постоянного. Нам же нужно приравнять переменный ток такому значению постоянного тока (3), чтобы количество выделяемой теплоты переменным током было таким же, что и при действии постоянного тока.

Действующая величина переменного тока I численно равна величине постоянного тока, который в одном и том же элементе цепи за время периода Т выделяет столько же теплоты, сколько при тех же условиях выделяет переменный ток.

Ясно, что действующее значение переменного тока будет меньше амплитудного значения. Определим количество теплоты, выделяемой за период Т постоянным током:

Q_пост = I²RT (5.21)

Для переменного тока та же величина будет:

(5.22)

Приравнивая оба тока найдем:

(5.23)

Т.е. действующая величина периодического тока является его средней квадратичной за период.

Найдем эту среднеквадратичную величину. Ее можно найти, решив полученное интегральное уравнение. Но мы поступим по другому: действующую величину переменного тока можно представить ввиде квадратного корня из суммы очень большого числа ординат кривой I_m²sin²ωt разделенной на число ординат:

(5.24)

где n → ∞; см. рисунок 5.7.

Рис.5.7 Определение действующего значения синусоидального тока

Рассмотрим два положения вектора I_m (2 и 8) - между ними 90^О.

Прямоугольные треугольники 6’ – 2 – 2’ & 6’ – 8 – 8’ равны. Из чего следует:

i₂² + i₈² = I_m² (5.25)

Для каждого положения вектора I_m в первой четверти можно найти соответствующее положение вектора во второй четверти, для которых можно написать аналогичное выражение. Такие же рассуждения можно провести для другой полуокружности, т.е распространить их на второй полупериод тока. Причем квадраты отрицательных мгновенных токов будут положительны. Поэтому:

(5.26)

Подставив полученное выражение в (5.24), получим:

(5.27)

Т.о. действующая величина синусоидального тока меньше его амплитуды в √2 раза.

Понятие о действующей величине можно распространить на все синусоидальные функции, а следовательно, можно говорить о действующих величинах напряжения, ЭДС, мощности.

Действующие величины токов и напряжений измеряются электроизмерительными приборами. Номинальные токи, мощности и напряжения оборудования выражаются действующими величинами.

Отношение амплитуды к действующей величине называется коэффициентом амплитуды К_а. Следовательно, для синусоиды:

(5.28)

По рассмотренному нами рисунку 5.7 можно определить среднюю величину синусоидального тока за полупериод.

Средней величиной переменного тока (ЭДС, напряжения) называется среднеарифметическое из всех мгновенных значений за полупериод.

Средняя величина равна высоте прямоугольника с основанием π (в радианах), площадь которого равна площади S, ограниченной полуволной синусоиды.

При этом (без вывода):

(5.29)

Отношение действующей величины к средней называется коэффициентом формы кривой

(5.30)

Для синусоиды К_ф = 1,11.