6. Методы решения задач с помощью аффинных преобразований

Задача 36[9]

Докажите, что медианы треугольника пересекаются в одной точке.

Решение

Из любого треугольника можно сделать равносторонний. Заметим, что середины сторон перешли в середины сторон и медианы перешли в медианы. В равностороннем треугольнике медианы пересекаются в одной точке в силу симметрии. Значит, в исходном треугольнике они тоже пересекались в одной точке.

Требуется обобщить результат задачи 36 на случай не обязательно медиан и не обязательно треугольников.

Следующая задача решается аналогичным образом.

Задача 37[9]

Докажите, что три медианы делят треугольник на 6 равновеликих треугольников.

Замечание. Обычно, задачу можно решить методом аффинных преобразований, если нужно найти отношение длин, или отношение площадей, или доказать параллельность. Причем в условии задачи не должно быть дано ничего такого, что не сохраняется при аффинных преобразованиях. Например, если в задаче дано точное значение какого-то угла, то, скорее всего, эта задача не решается методом аффинных преобразований.

Задача 38[9]

На сторонах треугольника поставлены точки, которые делят эти стороны в отношении . А именно, на стороне поставлена точка , на — точка , на — точка , и , , . Площадь треугольника равна 1. Чему равна площадь треугольника ?

Задача 39[10]

Докажите, что медианы треугольника .

Подсказка Превратите треугольник в правильный и используйте поворот вокруг центра на .

Задача 40[10]

Докажите, что медианы треугольника, образованного прямыми , , из предыдущей задачи, пересекаются в той же точке, что и медианы треугольника .

Задача 41[10]

Через каждую вершину треугольника проведены две прямые, делящие противоположную сторону треугольника на три равные части. Докажите, что диагонали, соединяющие противоположные вершины шестиугольника, образованного этими прямыми, пересекаются в одной точке.

Задача 42[11]

На сторонах AB, BC, CD параллелограмма ABCD взяты точки K, L, M соответственно, делящие эти стороны в одинаковых отношениях. Пусть b, c, d — прямые, проходящие через B,C,D параллельно прямым KL, KM, ML соответственно. Докажите, что прямые b, c, d проходят через одну точку.

Источник: ru.wikibooks.org

Дополнительный материал по аффинным преобразованиям.

Поворот плоскости и его матричное представление

Ниже речь пойдет о поворотах плоскости. С плоскостью все получается относительно несложно. Если мы делаем поворот относительно начала координат, то для задания вращения используется один угол (φ).

Прим. Принято считать направление вращения против часовой стрелки положительным. При этом удобно считать, что угол φ находится в интервале [–π; π].

Чтобы получить преобразование координат при повороте, возьмем произвольный вектор r, задающий некоторую точку. Его координаты:

При повороте на угол φ:

Т.о. при повороте на угол φ координаты x и y подвергаются преобразованию, написанному выше.

Прим. Здесь фактически была использована полярная система координат.

Матричное представление поворота плоскости

Написанное выше преобразование координат удобно представить в виде матрицы:

Прим. Умножение матриц производится по принципу строка на столбец. Поэтому количество столбцов (элементов в строке) в матрице слева должно совпадать с количеством строк (элементов в столбце) в матрице справа.

Какие преимущества дает матричное представление? Заметим, что если умножить две матрицы, задающие повороты на углы α и β, то получится матрица поворота на угол α + β. Это легко проверить, перемножив соответствующие матрицы и использовав формулы для косинуса и синуса суммы.

Аффинное преобразование и его матричное представление

Тема этого выпуска задание аффинного преобразования в матричной форме. Эта тема, по сути, является обобщением всего, что было сказано ранее.

Определение. Преобразование плоскости называется аффинным, если

• оно взаимно однозначно;

• образом любой прямой является прямая.

Преобразование называется взаимно однозначным, если

• разные точки переходят в разные;

• в каждую точку переходит какая-то точка.

Однородные координаты

Если рассмотреть параллельный перенос, то оказывается, что для его задания матрицы 2x2 уже недостаточно. Но его можно задать с помощью матрицы размера 3x3. Появляется вопрос, откуда взять третью координату у двумерной точки? 

Определение. Однородные координаты — координаты, обладающие тем свойством, что определяемый ими объект не меняется при умножении всех координат на одно и то же число.

Однородными координатами вектора (х, у) является тройка чисел (x', y', h), где х = х' / h, у = y'/h, а h — некоторое вещественное число (случай, когда h = 0 является особым).  

Прим. Данные координаты не позволяют однозначно задать точку плоскости. Например, (1, 1, 1) и (2, 2, 2) задают одну и ту же точку (1, 1). Предлагается взять набор (x, y, 1), который будет описывать все точки плоскости.

Матрица преобразования для однородных координат имеет размер 3х3. Рассмотрим некоторые преобразования в однородных координатах. 

Сжатие/растяжение

Это преобразование умножает соответствующие координаты точек на коэффициенты масштабирования по осям: (x, y) -> (a_x * x, a_y * y). Матрица преобразования запишется следующим образом:

[  a_x   0    0  ]     

[  0    a_y   0  ]

[  0    0    1  ] 

Где      a_x – растяжение по оси x,

a_y  – растяжение по оси y.

Прим. Можно заметить, что при отрицательных значениях коэффициентов сжатия/растяжения происходит отражение относительно соответствующих осей. Этот случай можно включить в данное преобразование, а можно вынести в отдельное, сказав, что коэффициенты масштабирования принимают только положительные значения.

Поворот

Матрица поворота 2x2 была подробно разобрана ранее. Теперь она дополняется строкой и столбцом:

[   cos(phi)    sin(phi)   0  ]                            

[  -sin(phi)    cos(phi)   0  ]

[   0           0          1  ] 

Прим. При угле phi = п эта матрица задает центральную симметрию относительно начала координат, которая является частным случаем поворота. Можно заметить, что такую симметрию можно задать с помощью преобразования сжатия/растяжения (допуская отрицательные коэффициенты масштабирования).

Параллельный перенос 

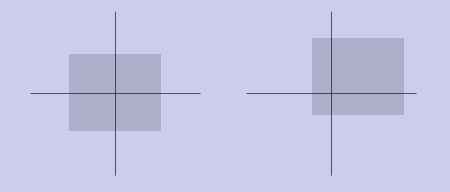
Исходный вектор (x, y) переходит в (x + tx, y + ty). Матрица преобразования запишется следующим образом: 

[  1    0    0  ]    

[  0    1    0  ]

[  t_x   t_y   1  ]

Отражение 

Как говорилось в примечании к преобразованию сжатия/растяжения, отражения получаются следующим образом:

[  -1    0    0  ]    

[   0    1    0  ]

[   0    0    1  ] отражение относительно оси x

[   1    0    0  ]    

[   0   -1    0  ]

[   0    0    1  ] отражение относительно оси y

Общий вид аффинного преобразования

Матрица 3x3, последний столбец которой равен ( 0  0  1 )^T, задает аффинное преобразование плоскости:

[   *    *    0  ]    

[   *    *    0  ]

[   *    *    1  ]

По одному из свойств, аффинное преобразование можно записать в виде:

f(x) = x * R + t,

где R – обратимая матрица 2x2, а t – произвольный вектор. В однородных координатах это запишется следующим образом:

[ R_1,1     R_1,2       0 ] 

[ R_2,1     R_2,2       0 ]

[ t_x       t_y        1 ]

Если умножить вектор-строку на эту матрицу получаем результат преобразования:

[ x   y   1 ]   *   [ R_1,1         R_1,2       0 ]

     [ R_2,1         R_2,2       0 ]

                    [ t_x           t_y        1 ]

=

[ x’   y’   1 ]   +   [ t_x   t_y    1 ]

При этом [ x’   y’ ]   =   R   *   [ x   y ]

Прим. Любопытный читатель уже задал себе вопрос: в чем смысл определителя матрицы R? При аффинном преобразовании площади всех фигур изменяются в |R|. (Можно строго доказать это с точки зрения математики, но здесь этот факт приводится без доказательства.)

Т.о. аффинное преобразование представляется в виде композиции некоторого преобразования, задаваемого матрицей R, и параллельного переноса. Разберем более подробно природу этой матрицы и возможности, которые она нам дает.

Матрица R определяет новый базис плоскости. Т.е. вектор (1, 0) переходит в (R_1,1, R_1,2), вектор (0, 1) переходит в (R_2,1, R_2,2). Новый базис это строки матрицы R.

Пример.

При отражении относительно оси y, базисный вектор по оси ординат сохраняется, а по оси абсцисс переходит в (-1, 0). Т.о. матрица R будет выглядеть следующим образом:

[  -1   0  ] [   0   1  ] Теперь становится ясно, что кроме вышеперечисленных преобразований, с помощью аффинного преобразования можно получить скос:

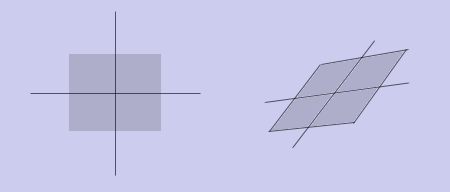Выше приведены базовые сведения о таком мощном инструменте, как аффинное преобразование. Остается много вопросов: какой подкласс аффинных преобразований сохраняет углы между прямыми? Как можно представить аффинное преобразование в виде композиции нескольких подклассов? Как задавать более сложные преобразования, например, осевая симметрия относительно произвольной прямой?

Ответы на эти вопросы и более детальное рассмотрение аффинного преобразования будут приведены отдельно, в качестве раздела курса теоретической геометрии.

Остановимся на практической реализации аффинного преобразования в виде демонстрационной программы. К возможностям приложения, демонстрирующего поворот плоскости мышью, добавляются функции параллельного переноса при нажатой клавише CTRL.

Т.к. эта статья является завершающей в данном разделе, код демонстрационного приложения должен быть соответствующим. Давайте попробуем разобраться, какие блоки нужны в графическом приложении, параллельно рассматривая, как они реализованы в данной программе:

• блок, в котором происходит создание окна и обрабатываются сообщения операционной системы, реализован в файлe main.cpp

• графический движок, выполняющий отрисовку изображения, класс Engine

• прослойка, необходимая для преобразования логических координат в оконные и обратно, класс Viewport

• объект, отвечающий за реакцию на действия пользователя, класс Action

В приведенном примере реализованы эти функциональные блоки, с подробными комментариями.

Векторы в пространстве. Однородные координаты. Матрицы преобразований

Вектор в трехмерном пространстве

Вектор в трехмерном пространстве определяется тремя координатами p(x, y, z). При рассмотрении двумерных преобразований вводились однородные координаты. Также будет удобно ввести их при рассмотрении трехмерного пространства. Как мы увидим в дальнейшем, их использование позволяет задавать аффинные и нелинейные преобразования (например, перспективное) в виде матриц, что позволяет создавать весьма эффективные и простые реализации.

Прим. Понятия - точка и вектор. Точка это тоже вектор: если совместить его начало с началом координат, то конец будет находиться в определяемой им точке. Но также существуют вектора в классическом смысле, например вектор нормали. О чем конкретно идет речь будет понятно из контекста. В рамках данной лекции вектор подразумевается в смысле вектор-точка.

Однородные координаты

Определение. Однородные координаты — координаты, обладающие тем свойством, что определяемый ими объект не меняется при умножении всех координат на одно и то же число.

Однородными координатами вектора (х, у, z) является тройка чисел (x', y', z', w), где х = х' / w, у = y' / w, z = z' / w, а w — некоторое вещественное число (случай, когда w = 0 является особым).

Данные координаты не позволяют однозначно задать точку пространства. Например, (1, 1, 1, 1) и (2, 2, 2, 2) задают одну и ту же точку (1, 1, 1). При переходе к однородным координатам для точки с координатами (x, y, z) предлагается взять набор (x, y, z, 1). В процессе преобразований координата w может меняться. Обратный переход к декартовым координатам осуществляется посредством деления на w-координату.

Матрицы преобразований в трехмерном пространстве

Матрица преобразования для однородных координат имеет размер 4х4. Рассмотрим пример матричного преобразования в однородных координатах.

         |   2    0    0    1    |

M    =   |   0    3    0    2    |

         |   0    0    1   -1    |

         |   0    0    0    1    |

x' = 2 * x + 1

y' = 3 * y + 2

z' = 1 * z – 1

w' = 1

Данная матрица определяет следующее преобразование: растяжение по оси x в два раза, по оси у в три раза и перенос на вектор (1, 2, -1). При этом матрица M применяется к вектору-столбцу слева:

             | M₁₁  M₁₂  M₁₃  M₁₄ |   | p_x | 

p' = M * p = | M₂₁  M₂₂  M₂₃  M₂₄ | * | p_y |

             | M₃₁  M₃₂  M₃₃  M₃₄ |   | p_z | 

             | M₄₁  M₄₂  M₄₃  M₄₄ |   | 1  | 

Заметим, что вектор p' также представляет собой вектор-столбец. На самом деле возможны две, равноправные с точки зрения математики, записи:

1)      Вектор записывается как столбец:

|    2    0    0    1    |     | x |     | 2 * x + 1 |

|    0    3    0    2    |  *  | y |  =  | 3 * y + 2 |

|    0    0    1   -1    |     | z |     | 1 * z – 1 | 

|    0    0    0    0    |     | 1 |     |     1     |

2)      Вектор записывается как строка, матрица транспонируется:

     |    2    0    0    0    |

        | x  y  z  1 |  *   |    0    3    0    0    |

  |    0    0    1    0    |

  |    1    2   -1    0    |

 

=  | 2 * x + 1    3 * y + 2    1 * z – 1    1 |

C точки зрения самого преобразования эти записи эквивалентны. Какую из них использовать – это вопрос договоренности. На практике, и в OpenGL и в DirectX используется первый вариант, с учетом того, что матрицы укладываются в памяти по столбцам. Т.е. матрица

| M₁₁  M₁₂  M₁₃  M₁₄ |

| M₂₁  M₂₂  M₂₃  M₂₄ |

| M₃₁  M₃₂  M₃₃  M₃₄ |

| M₄₁  M₄₂  M₄₃  M₄₄ |

в линейной памяти будет выглядеть следующим образом:

            M₁₁ M₂₁ M₃₁ M₄₁ M₁₂ M₂₂ M₃₂ M₄₂ M₁₃ M₂₃ M₃₃ M₄₃ M₁₄ M₂₄ M₃₄ M₄₄

В трехмерной математике также принято использовать первый вариант записи.

Прим. Иногда, в теоретическом разделе будут встречаться похожие вставки, относящиеся к практике. В основном это будет касаться принятых обозначений.

Матрица не аффинного преобразования

Продемонстрируем матрицу, которая не сохраняет параллельность прямых (матрицу не аффинного преобразования). Примером может служить простейшая матрица перспективного преобразования, которая будет рассмотрена позже более подробно. Пока что просто покажем, как можно использовать однородные координаты для записи нелинейных преобразований.

|    1    0    0    0    |

M_proj =    |    0    1    0    0    |

|    0    0    1    0    |

|    0    0    -1    0    |

| x |     |  x  |

p_proj = M_proj * p = M_proj *   | y |  =  |  y  |

| z |     |  z  |

| 1 |     | -z  |

p_proj = ( -x / z, -y / z, -1, 1 )

Прим. Последняя строка как раз и определяет вид изменений w-координаты исходного вектора.

Резюме

В этой статье мы ввели основные математические объекты и договоренности о записи, которые понадобятся нам для построения дальнейшей теории. Более сложные объекты, например, кватернионы, будут введены и подробно описаны в отдельной главе.

Далее нам потребуются следующие вещи, непосредственно связанные с матрицами:

• Аффинные преобразования в трехмерном пространстве и их матричная запись.

• Точечные преобразования. Преобразования локальной системы координат. Связь между ними.

Аффинные преобразования пространства

При работе с трехмерными объектами, часто требуется совершать по отношению к ним различные преобразования: двигать, поворачивать, сжимать, растягивать, скашивать и т.д. При этом в большинстве случаев требуется, чтобы после применения этих преобразований сохранялись определенные свойства.

Определение. Преобразование плоскости называется аффинным (от англ. affinity – родство), если

• оно взаимно однозначно;

• образом любой прямой является прямая.

Преобразование называется взаимно однозначным, если

• разные точки переходят в разные;

• в каждую точку переходит какая-то точка.

Свойства аффинного преобразования в трехмерном пространстве:

• отображает n-мерный объект в n-мерный: точку в точку, линию в линию, поверхность в поверхность;

• сохраняет параллельность линий и плоскостей;

• сохраняет пропорции параллельных объектов – длин отрезков на параллельных прямых и площадей на параллельных плоскостях.

Любое аффинное преобразование задается матрицей 3x3 с ненулевым определителем и вектором переноса:

Посмотрим на это с точки зрения математики. R представляет собой матрицу линейного оператора над пространством трехмерных векторов. Вектор T требуется для осуществления параллельного переноса: если помножить ( 0  0  0 ) на любую матрицу 3x3, опять получим ( 0  0  0 ) – начало системы координат, относительно преобразования R, является неподвижно точкой. Требование, чтобы определитель был ненулевой, диктуется определением. По сути, если определитель матрицы R равен нулю, то всё пространство переходит в плоскость, прямую или точку. Тем самым не соблюдается взаимная однозначность.

На практике удобно задавать аффинное преобразование одной матрицей. При этом используются однородные координаты, введенные в предыдущей статье. Аффинное преобразование будет задаваться следующей матрицей 4x4:

Заметим, что первые три значения последней строки равны 0. Это необходимое условие того, что преобразование будет аффинным. В общем случае произвольная матрица размера 4x4 задает проективное преобразование. Такие преобразования, как можно догадаться из названия, используются для проецирования трехмерной сцены. Подробнее об этом будет рассказано в одной из последующих статей.

Рассмотрим частные случаи аффинных преобразований.

Прим. Здесь и в дальнейшем будет использоваться система координат, введенная следующим образом:

• система координат правая;

• ось z направлена на наблюдателя, перпендикулярно плоскости экрана;

• ось y находится в плоскости экрана и направлена вверх;

• ось x находится в плоскости экрана и направлена вправо.

Подробнее мы остановимся на этом при рассмотрении геометрического конвейера.

Параллельный перенос

Исходный объект	Параллельный перенос

Матрица этого преобразования выглядит следующим образом:

В данном случае матрица R = E, единичной матрице.

Преобразования, рассматриваемые ниже, затрагивают только матрицу R, поэтому будет указываться только она.

Поворот (вращение)

Исходный объект	Поворот вокруг некоторого вектора

Если на плоскости повороты делались вокруг некоторой точки, то в трехмерном пространстве повороты производятся вокруг некоторого вектора. Перед тем, как перейти к построению матрицы поворота вокруг произвольного вектора, рассмотрим частные случаи поворотов вокруг координатных осей.

Прим. Поворот вокруг произвольного вектора не равно поворот вокруг произвольной направленной прямой.

Поворот вокруг оси y

Исходный объект	Поворот вокруг оси y

Заметим, что при повороте вокруг оси y ординаты точек (у-координаты) не меняются. Также стоит отметить, что координаты x и z точки преобразуются независимо от y-координаты. Это означает, что любая точка p(x, y, z) перейдет в точку p’(x’(x, z), y, z’(x, y)). Теперь осталось понять, как преобразуются координаты x и z: в плоскости Oxz это будет поворот вокруг начала координат по часовой стрелке (т.к. x z y - левая тройка), т.е. в отрицательном направлении. Матрица такого преобразования известна (см. Поворот плоскости):

В итоге:

Матрица преобразования R_y(φ_y):

Поворот вокруг осей x и z

Поворот вокруг оси x	Поворот вокруг оси z

Аналогичными рассуждениями можно получить матрицы поворотов R_x(φ_x) и R_z(φ_z)вокруг осей x и z, соответственно.

Приведём окончательные результаты:

Несложно заметить, что определители матриц R_x, R_y, R_z равны 1. Также матрицы вращений R_rot обладают свойством ортогональности: R^TR = RR^T = E. Из этого, в свою очередь, следует полезное свойство, что обращение матрицы поворота можно заменить транспонированием: R^-1(φ) = R^T(φ).

Масштабирование (сжатие/растяжение, отражение)

Исходный объект	Масштабирование

Коэффициенты сжатия/растяжения, по аналогии с двухмерным пространством, определяются диагональными членами матрицы R:

Результат:

Комбинация коэффициентов s_x = -1, s_y = 1, s_z = 1 будет задавать отражение от плоскости Oyz (x = 0). При s_x = s_y = s_z = -1 получим центральную симметрию относительно начала координат.

Интерпретация матрицы R

Рассмотрим, что представляет собой матрица R с точки зрения линейной алгебры. Оказывается, что матрица R содержит базис новой системы координат.

Действительно, матрица

( R₁₁    R₁₂    R₁₃ )

( R₂₁    R₂₂    R₃₃ )

( R₃₁    R₃₂    R₃₃ )

переводит вектора декартова базиса:

( 1  0  0 ) → ( R₁₁  R₂₁  R₃₁ )

( 0  1  0 ) → ( R₁₂  R₂₂  R₃₂ )

( 0  0  1 ) → ( R₁₃  R₂₃  R₃₃ )

Скос (сдвиг)

Исходный объект	Скос (сдвиг)

Теперь несложно получить преобразование скоса. Например:

Прим. Если придерживаться общепринятой терминологии, то приведенное выше преобразование называется сдвигом. Сдвигом (shear) будет  любое преобразование, главная диагональ матрицы R которого единичная. Если при этом определитель матрицы R равен нулю, то преобразование не является аффинным.

Сложные аффинные преобразования

Сложные аффинные преобразования можно получить как комбинацию простых (элементарных) преобразований. При этом выбирать простые аффинные преобразования можно по разному. Например, поворот можно представить как комбинацию масштабирования и сдвига. Тем не менее, для удобства, поворот также считается элементарным преобразованием. Поворот вокруг произвольного вектора представляется как комбинация поворотов вокруг координатных осей. Об этом будет подробно рассказано в следующей статье.