1Анализ задачи
1.1 Описание предметной области
Метод трапеций
Криволинейной трапецией называют часть плоскости, ограниченную снизу Ох, а сверху дугой ab (некоторой линией, уравнением которой является y=f(x)), слева и справа прямыми x=a и x=b.
Площадь под кривой заменяется суммой площадей трапеций:
или
Нетрудно
убедиться, что
Поскольку точность вычислений по приведенным формулам зависит от числа разбиений n исходного отрезка [a; b], то вычислительный процесс целесообразно строить итерационным методом, увеличивая n до тех пор, пока не будет выполнено условие
<
где
– значения интеграла на
шаге, а
– точность вычислений.
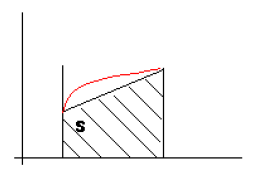
Рисунок 1.1.1 – Графическое изображение метода трапций
Вычисление методом трапеций
Для того чтобы вычислить интеграл по методу трапеций, необходимо определить число n - частей, на которые необходимо разбить криволинейную трапецию, чтобы достичь требуемой точности (три знака после запятой).
Предположим, есть некая криволинейная трапеция. Разбиваем криволинейную трапецию сначала на произвольное число частей n, то есть получаем n1- обыкновенных трапеций. Рассчитываем суммарную площадь трапеций (S1). Далее разбиваем криволинейную трапецию на n2>n1 частей и также рассчитываем суммарную площадь трапеций (S2). Следующий шаг – вычисление разности S2-S1. Если S2-S1<=0.001, то вычисления можно прервать и взять за искомую площадь (значение интеграла) площадь S
Если S2-S1>0.001, то S1:=S2, N1:=N2,N2:=N2*2, до тех пор, пока не будет достигнута требуемая точность.
Метод средних прямоугольников
Вычисление определенного интеграла геометрически означает вычисление площади фигуры, ограниченной кривой , прямыми х=а и х=b и осью абсцисс. Приближенно эта площадь равна сумме площадей прямоугольников.
Обозначим
,
где
n – количество шагов.
Формула левых прямоугольников:
Формула правых прямоугольников:
Более точной является формула средних прямоугольников:
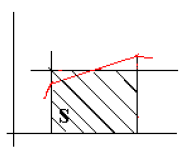
Рисунок 1.1.2 – Графическое отображение метода прямоугольников
Метод Ньютона-Котеса
Заменим подынтегральную функцию f(x) интерполяционным многочленом Лагранжа:
.
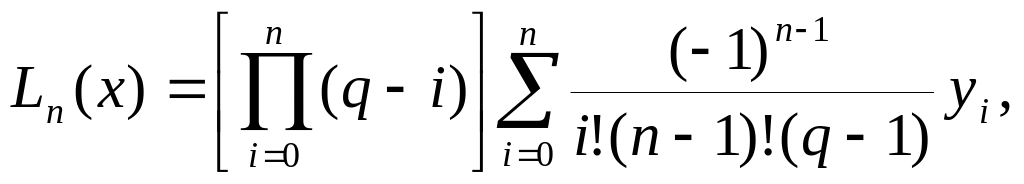
Тогда
;
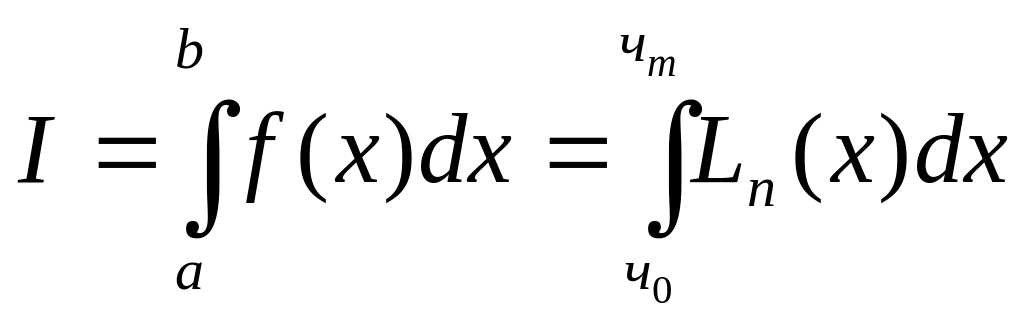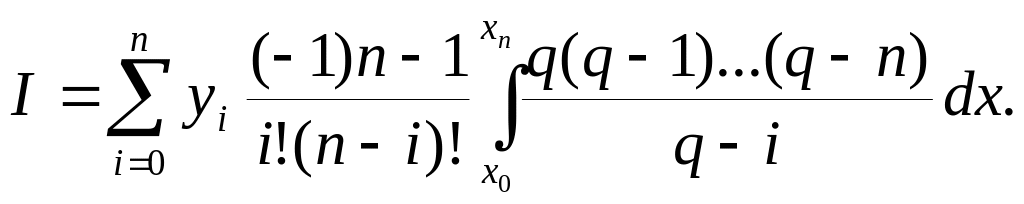
Так как dx=hdq, то
Так как , то
Окончательно получаем формулу Ньютона-Котеса:
Величины Hi называют коэффициентами Ньютона-Котеса. Они не зависят от f(x). Их можно вычислить заранее для различного числа узлов n. Формула Ньютона-Котеса с n узлами точна для полиномов степени не выше n. Для получения большей точности не рекомендуется использовать формулы с большим числом узлов, а лучше разбивать отрезок на подотрезки, к каждому из которых применяется формула с одним и тем же небольшим числом узлов.
Интересно отметить, что из формулы следуют как частные случаи: формула трапеций при n=1
;
формула Симпсона при n=2
;
правило трех восьмых при n=3
.
При n>6 формулу не применяют, так как коэффициенты Ньютона-Котеса становятся слишком большими и вычислительная погрешность резко возрастает.
Рисунок 1.1.3 – Графическое отображение метода Ньютона-Котеса