ФЕДЕРАТИВНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ

ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

Курсовая работа

По информатике

Факультет: ЛА Преподаватель:

Группа: СЭ-11 Помадин С.А.

Студент: Кочурова Н.М. Отчёт сдан:

Зачтено:

Дата: 30.04.12

Подпись:

Новосибирск

2012г.

Содержание

1.1 Постановка задачи 3

1.1.1 Цель работы 3

1.1.2 Обобщённая формулировка задачи 3

1.2. Анализ задачи 4

1.2.1 Метод бисекции 4

1.2.2 Метод Ньютона 6

1.2.3 Математическое решение задачи 7

1.3 Решение путём написания программы 8

1.3.1 Блок схема программы и блок-схемы алгоритма поиска 8

решения 8

1.3.3 Тексты программы 13

1.3.4 Тестовая задача и результаты прогона тестовой задачи 15

1.4 Решение таблицей в Excel 17

1.4.1 Структура таблицы 17

1.4.2 Таблица в виде формул 17

1.4.3 Макрос 18

1.4.4 Таблица результатов 19

Стоит отметить, что 10 значений явно недостаточно для определения точного результата, который, судя по таблице, расположен в диапазоне [-7.8; -7.72]. 20

1.4.5 График результатов 21

1.4.6 Методика применения таблицы 22

1.5. Выводы 23

1.5.1 Сравнение результатов 23

1.5.2 Сравнение методов решения 23

1.5.3 Рекомендации по области применения методов 24

2. Основы векторной и растровой графики 25

2.1 Постановка задачи 25

2.1.1 Цель работы 25

2.1.2 Обобщённая формулировка задачи 25

2.2 Векторная 2D графика 26

2.2.1 Анализ чертежа 26

2.2.2 Описание построения чертежа 26

2.2.3 Чертёж, вставленный в формате GIF 27

2.2.4 Чертёж вставленный в Word, в формате WMF 28

2.2.5 Сравнительный анализ качества преобразования изображения 29

2.3 Векторная 3D графика 29

2.3.1 Анализ формы модели 29

2.3.2 Описание построения модели 29

3. Заключение 30

1. Основы программирования и численных алгоритмов

1.1 Постановка задачи

1.1.1 Цель работы

• Закрепить навыки:

  1. работы с системами программирования.

  2. описания алгоритмов на алгоритмическом языке.

• Обобщить знания об алгоритмах, используемых в численных методах.

• Применить на практике знания об алгоритмах, используемых в численных методах, с использованием различных прикладных программ.

  1. Закрепить навыки применения электронных таблиц для обработки и представления численных данных.

1.1.2 Обобщённая формулировка задачи

-Решить задачу численным методом:

a) Написать программу на языке Pascal, вычисляющую решение

итерационным методом с задаваемой точностью и границами интервала.

b) Построить в Excel таблицу с требуемой точностью, построить график функции и найти решение, используя график, затем, найти решения, используя функции поиска.

-Сравнить результаты, сделать выводы. Выводы иллюстрировать диаграммами Excel.

Заданная функция:

1.2. Анализ задачи

Задача была реализована с помощью двух численных методов: метода бисекций и метода Ньютона. Рассмотрим каждый из них по отдельности.

1.2.1 Метод бисекции

Метод бисекции или метод деления отрезка пополам  простейший численный метод для решения нелинейных уравнений вида f(x)=0. Предполагается только непрерывность функции f(x). Поиск основывается на теореме о промежуточных значениях.

Алгоритм основан на следующем следствии из теоремы Больцано — Коши:

Пусть непрерывная функция  , тогда, если  , то  .

Таким образом, если мы ищем ноль, то на концах отрезка функция должна быть противоположных знаков. Разделим отрезок пополам и возьмём ту из половинок, на концах которой функция по-прежнему принимает значения противоположных знаков. Если значение функции в серединной точке оказалось искомым нулём, то процесс завершается.

Точность вычислений задаётся одним из двух способов:

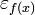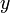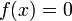1.  по оси  , что ближе к условию   из описания алгоритма; или

2. , по оси 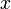 , что может оказаться удобным в некоторых случаях.

Процедуру следует продолжать до достижения заданной точности.

Для поиска произвольного значения достаточно вычесть из значения функции искомое значение и искать ноль получившейся функции.

Задача заключается в нахождении корней нелинейного уравнения

Для начала итераций необходимо знать отрезок   значений  , на концах которого функция принимает значения противоположных знаков.

Противоположность знаков значений функции на концах отрезка можно определить множеством способов. Один из множества этих способов — умножение значений функции на концах отрезка и определение знака произведения путём сравнения результата умножения с нулём:

в действительных вычислениях такой способ проверки противоположности знаков при крутых функциях приводит к преждевременному переполнению.

Для устранения переполнения и уменьшения затрат времени, т.е. для увеличения быстродействия, на некоторых программно-компьютерных комплексах противоположность знаков значений функции на концах отрезка нужно определять по формуле:

так как одна операция сравнения двух знаков двух чисел требует меньшего времени, чем две операции: умножение двух чисел (особенно с плавающей запятой и двойной длины) и сравнение результата с нулём. При данном сравнении, значения функции   в точках  и   можно не вычислять, достаточно вычислить только знаки функции   в этих точках, что требует меньшего машинного времени.

Из непрерывности функции   и условия (2.2) следует, что на отрезке   существует хотя бы один корень уравнения (в случае не монотонной функции   функция имеет несколько корней и метод приводит к нахождению одного из них).

Найдём значение   в середине отрезка:

в действительных вычислениях, для уменьшения числа операций, в начале, вне цикла, вычисляют длину отрезка по формуле:

а в цикле вычисляют длину очередных новых отрезков по формуле:   и новую середину по формуле:

Вычислим значение функции   в середине отрезка  :

Если   или, в действительных вычислениях,  , где   — заданная точность по оси  , то корень найден.

Иначе   или, в действительных вычислениях,  , то разобьём отрезок   на два равных отрезка:   и  .

Теперь найдём новый отрезок, на котором функция меняет знак:

Если значения функции на концах отрезка имеют противоположные знаки на левом отрезке,   или  , то, соответственно, корень находится внутри левого отрезка  . Тогда возьмём левый отрезок присвоением  , и повторим описанную процедуру до достижения требуемой точности   по оси  .

Иначе значения функции на концах отрезка имеют противоположные знаки на правом отрезке,   или  , то, соответственно, корень находится внутри правого отрезка  . Тогда возьмём правый отрезок присвоением  , и повторим описанную процедуру до достижения требуемой точности   по оси  .

За количество итераций   деление пополам осуществляется   раз, поэтому длина конечного отрезка в   раз меньше длины исходного отрезка.

Существует похожий метод, но с критерием останова вычислений   по оси  ^[1], в этом методе вычисления продолжаются до тех пор, пока, после очередного деления пополам, новый отрезок больше заданной точности по оси  :  . В этом методе отрезок на оси   может достичь заданной величины  , а значения функций   (особенно крутых) на оси   могут очень далеко отстоять от нуля, при пологих же функциях   этот метод приводит к большому числу лишних вычислений.

В дискретных функциях   и   - это номера элементов массива, которые не могут быть дробными, и, в случае второго критерия останова вычислений, разность  не может быть меньше  .