Тема 1. Задачи, приводящие к уравнениям различных типов.
Преобразовать уравнение к каноническому виду
Решение
Т.к. Возможны 3 случая
y=0 – параболический тип. Канонический вид:
y>0 – гиперболический тип.
Запишем ДУ характеристик:
Решение:
Введем новые переменные:
Запишем производные:
Аналогично
Перепишем левую часть уравнения для новых переменных:
Т.к. , то канонический вид уравнения:
y<0 – эллиптический тип.
Запишем ДУ характеристик:
Решение:
Введем новые переменные:
Аналогично запишем производные и уравнение в новых переменных:
- канонический вид уравнения:
Тема 3. Метод разделения переменных для решения краевых задач.
Дан тонкий однородный стержень (0 < x < π), боковая поверхность которого теплоизолирована. Найти распределение температуры u(x, t) в стержне, если концы стержня поддерживаются при постоянной температуре
начальная температура
Решение:
Уравнение теплопроводности:
,
начальные и краевые условия:
Будем искать решение в виде:
где
-
непрерывная функция, имеющая первую и
вторую производные и удовлетворяющая
краевым условиям:,
.
Тогда составим уравнение для w(x,t):
,
Имеем
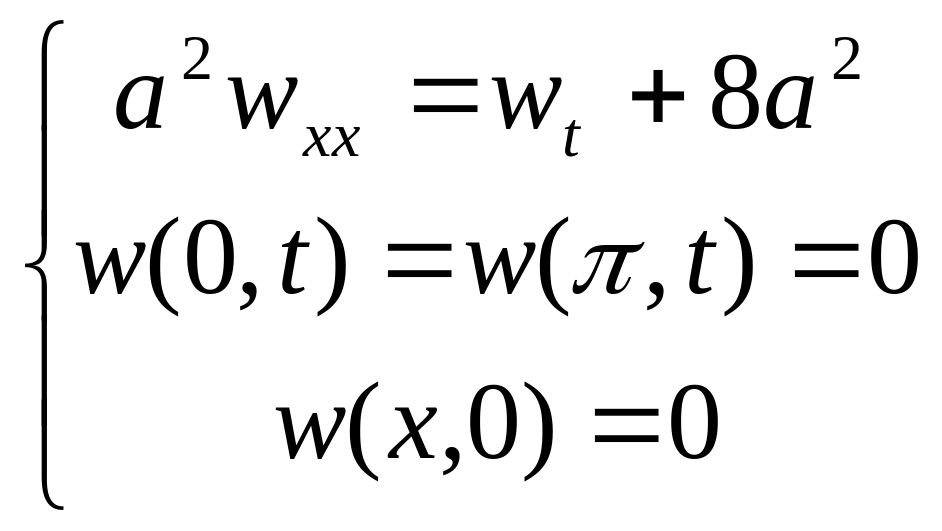
Решение ищем в классе функций:
,
Разделяя переменные, получим собственные
значения и соотв. собственные функции
Второе уравнение:
Общее решение
,
Подставляем в уравнение для нахождения
Из начальных условий:
Тогда
.
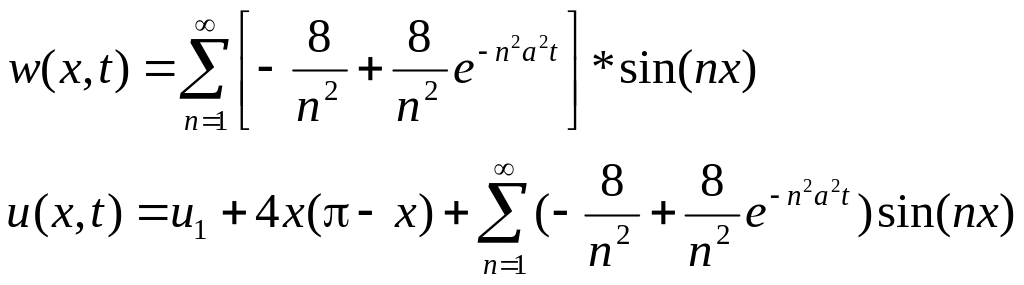БИЛЕТ 18
Тема 2. Решения задачи Коши для волнового уравнения.
Бесконечная струна возбуждена ударом так что начальная скорость отлична от нуля на отрезке , где она принимает постоянное значение . Построить профиль струны для моментов времени (k = 1,2,3,4,5,6,7,8).
Решение
Уравнение малых поперечных колебаний: .
Формула Даламбера:
где и
Получаем:
Решение есть суперпозиция 2х волн: прямой и обратной.
Условия сшивания:
, в точке x=-c.
, в точке x=c.
Получаем, что , , в точке x=-c
Тогда решение:
Тема 3. Метод разделения переменных для решения краевых задач.
Найти закон свободных
колебаний круглой мембраны радиусом
1, закреплённой по контуру, если
,
начальное отклонение имеет форму
,
а начальная скорость равна нулю.
Решение
Уравнение свободных колебаний (Лапласиан запишем в полярной системе координат)
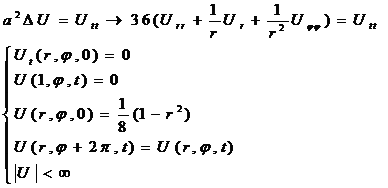
Решаем методом разделения переменных (методом Фурье):
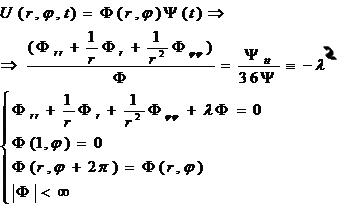
Пусть
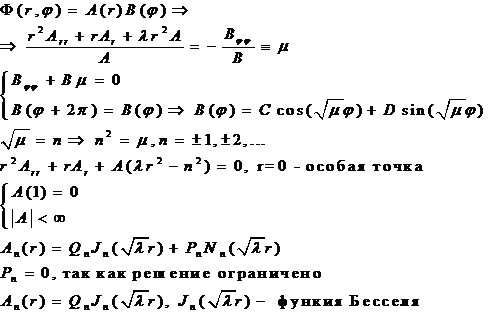
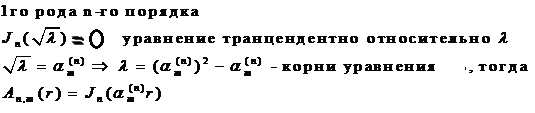
Получаем
,
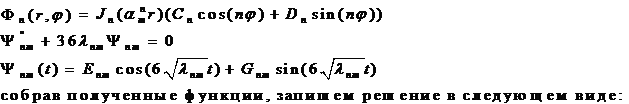
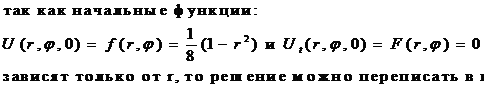
Причем все
,
а
.
БИЛЕТ 19
Тема 3. Метод разделения переменных для решения краевых задач.
Однородная струна, закрепленная на концах х = 0 и x = l , имеет в начальный момент форму параболы, симметричной относительно перпендикуляра, проведенного через точку x = l/2. Определить смещение точек струны от прямолинейного положения равновесия, предполагая, что начальные скорости отсутствуют.
Решение:
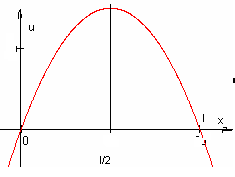
Уравнение струны:
Запишем краевые условия: u(0,t) = u(l,t) = 0.
Так как начальные скорости отсутствуют,
то
.
Найдем начальное условие:
Уравнение параболы:
,
u(0)=с =0,
=>
.
Тогда начальное условие имеет вид:
Имеем уравнение гиперболического типа.
Представим решение как произведение
двух функций
,
подставим в уравнение:
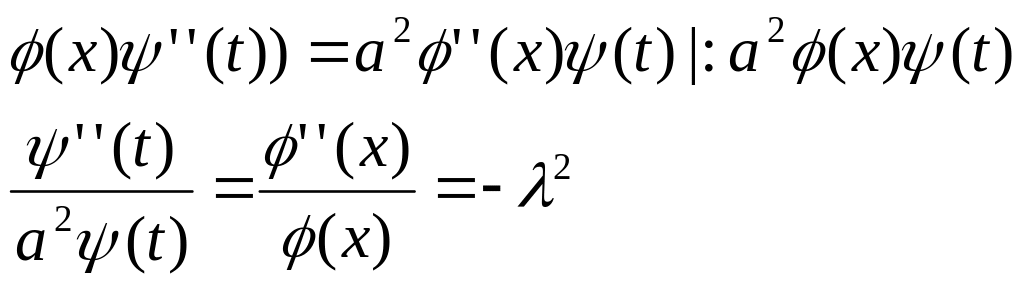
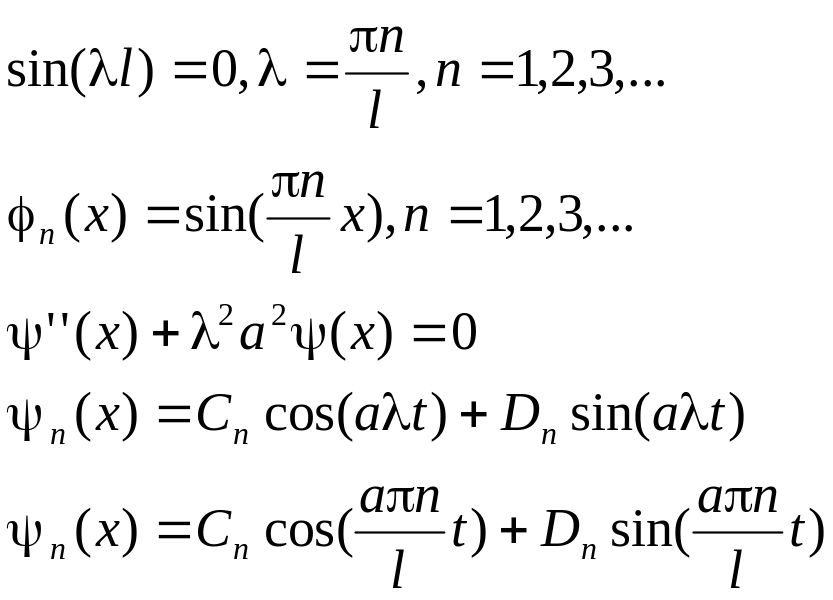
Коэффициенты находим из свойства ортогональности и граничных условий
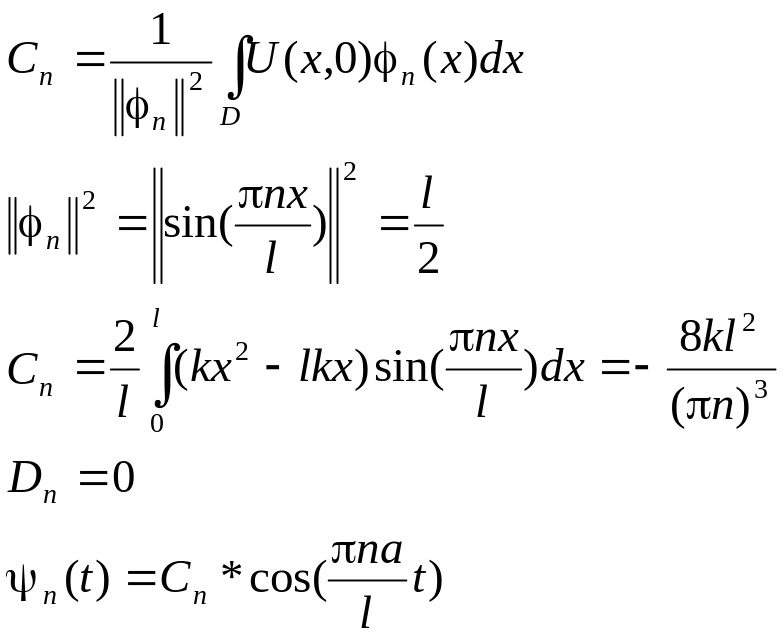
Тогда решение задачи запишем:
