- •Тема 1. Задачи, приводящие к уравнениям различных типов.
- •Тема 3. Метод разделения переменных для решения краевых задач.
- •Тема 1. Задачи, приводящие к уравнениям различных типов.
- •Тема 3. Метод разделения переменных для решения краевых задач.
- •Тема 1. Задачи, приводящие к уравнениям различных типов.
- •Тема 3. Метод разделения переменных для решения краевых задач.
- •Тема 1. Задачи, приводящие к уравнениям различных типов.
- •Тема 3. Метод разделения переменных для решения краевых задач.
- •Билет №5
- •Тема 1. Задачи, приводящие к уравнениям различных типов.
- •Тема 3. Метод разделения переменных для решения краевых задач.
- •Тема 2. Решения задачи Коши для волнового уравнения.
- •Тема 5. Метод функций Грина решения краевых задач для уравнений эллиптического типа.
- •Тема 1. Задачи, приводящие к уравнениям различных типов.
- •Тема 3. Метод разделения переменных для решения краевых задач.
- •Тема 2. Решения задачи Коши для волнового уравнения.
- •Тема 3. Метод разделения переменных для решения краевых задач.
- •Тема 3. Метод разделения переменных для решения краевых задач.
- •Тема 5. Метод функций Грина решения краевых задач для уравнений эллиптического типа.
- •Тема 1. Задачи, приводящие к уравнениям различных типов.
- •Тема 3. Метод разделения переменных для решения краевых задач.
- •Тема 1. Задачи, приводящие к уравнениям различных типов.
- •Тема 3. Метод разделения переменных для решения краевых задач.
- •Тема 1. Задачи, приводящие к уравнениям различных типов.
- •Тема 3. Метод разделения переменных для решения краевых задач.
- •Тема 1. Задачи, приводящие к уравнениям различных типов.
- •Тема 3. Метод разделения переменных для решения краевых задач.
- •Тема 1. Задачи, приводящие к уравнениям различных типов.
- •Тема 3. Метод разделения переменных для решения краевых задач.
- •Тема 3. Метод разделения переменных для решения краевых задач.
- •Тема 5. Метод функций Грина решения краевых задач для уравнений эллиптического типа.
- •Тема 3. Метод разделения переменных для решения краевых задач.
- •Тема 5. Метод функций Грина решения краевых задач для уравнений эллиптического типа.
- •Тема 1. Задачи, приводящие к уравнениям различных типов.
- •Тема 3. Метод разделения переменных для решения краевых задач.
- •Тема 2. Решения задачи Коши для волнового уравнения.
- •Тема 3. Метод разделения переменных для решения краевых задач.
- •Тема 3. Метод разделения переменных для решения краевых задач.
- •Тема 5. Метод функций Грина решения краевых задач для уравнений эллиптического типа.
- •Тема 1. Задачи, приводящие к уравнениям различных типов.
- •Тема 3. Метод разделения переменных для решения краевых задач.
Тема 3. Метод разделения переменных для решения краевых задач.
Найти колебания однородной струны 0 х l с закрепленными концами, вызванные начальным смещением:
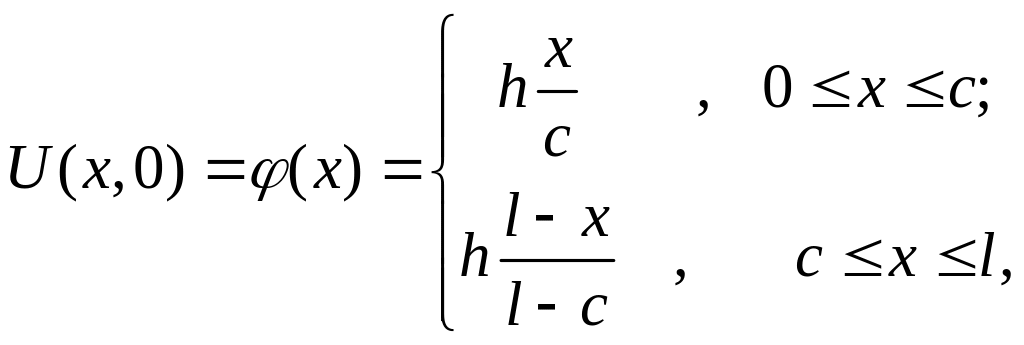
где h – малое число. Начальные скорости точек струны равны нулю.
Решение:
Запишем математическую постановку задачи:
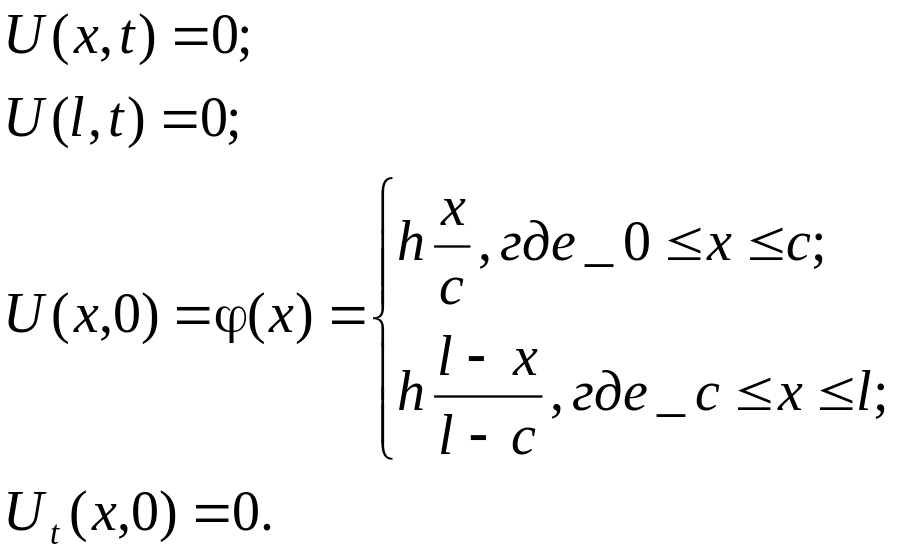
Уравнение малых колебаний
![]() .
.
Решаем методом Фурье (т.е. разделяем переменные)
.
Подставляем, преобразуем:
, ,
Получаем
![]() -
задача Штурма–Лиувилля:
-
задача Штурма–Лиувилля:
Решение этого уравнения в общем виде
![]()
Из начальных и краевых условий:
Отсюда собственные функции (с точностью до произвольного постоянного множителя):
.
Из второго уравнения:
![]() .
.
Решение этого ДУ:
![]()
Тогда решение:
![]()
Из начального условия
![]() все
все
![]() .
.
Найдем
![]() из принципа ортогональности и граничных
условий:
из принципа ортогональности и граничных
условий:
![]()
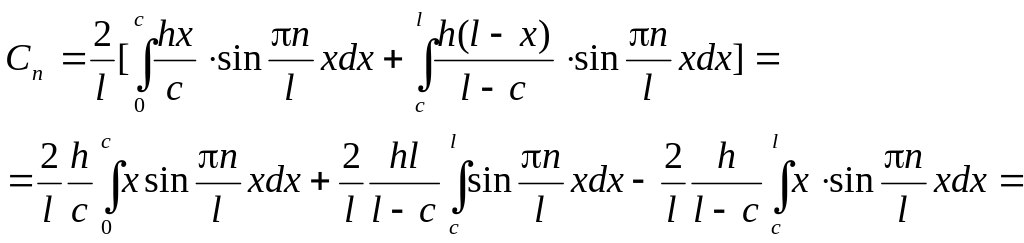 .
.
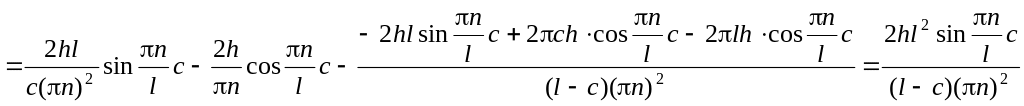
Тогда решение:
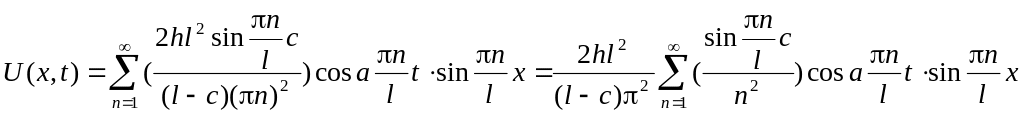
Билет №5
Тема 1. Задачи, приводящие к уравнениям различных типов.
Определить тип уравнения с частными производными 2uyy-uxy+3ux-u=0.
Решение
Классификация уравнений и принадлежность их к тому или иному типу определяется в зависимости от коэффициентов при старших производных. В общем виде уравнение имеет следующий вид:
=0
Любое такое уравнение можно привести к каноническому виду. Классификация производится в зависимости от дискриминанта :
Если дискриминант больше нуля, то уравнение считается гиперболическим в области D,
Если дискриминант меньше нуля, то уравнение считается эллиптическим в области D,
Если же дискриминант равен нулю, то уравнение считается параболическим в области D.
Определим тип нашего уравнения. В данном
уравнение имеем следующие коэффициенты:
a11=0, a12=-1/2, a22=2, найдем дискриминант
уравнения
![]() =>
=>
уравнение относится к гиперболическому типу.
Тема 3. Метод разделения переменных для решения краевых задач.
Решить задачу о малых поперечных колебаниях круглой мембраны радиуса R, закрепленной по краям, под действием начального возмущения:
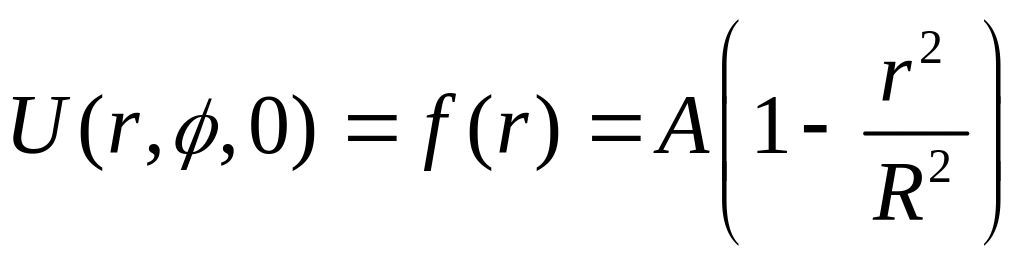 ;
;
![]() .
.
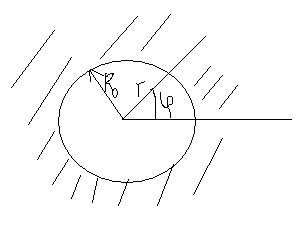
![]()
![]() - условие периодичности.
- условие периодичности.
Уравнение малых поперечных колебаний:
![]()
Запишем Лапласиан в полярной системе координат:
![]()
Будем решать методом Фурье: Разделим
переменные
![]() ,
,
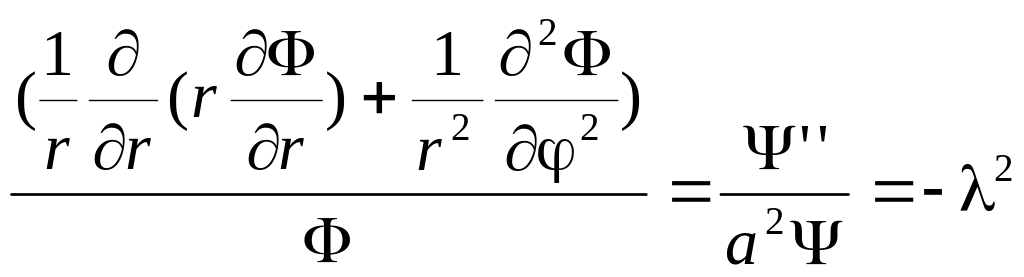
Отсюда
![]()
А т.к. начальные условия не зависят от
угла, то
![]() .
.
![]() - уравнение Бесселя
- уравнение Бесселя
Граничное условие
![]()
Добавляем естественное дополнительное условие:
![]()
Общее решение данной задачи представляется с использованием специальной цилиндрической функции – функции Бесселя
![]()
Из условия ограниченности получим, что
все
![]() ,
т.к.
,
т.к.
![]() .
.
Из граничного условия:
![]()
![]() ,
m=1,2…
,
m=1,2…
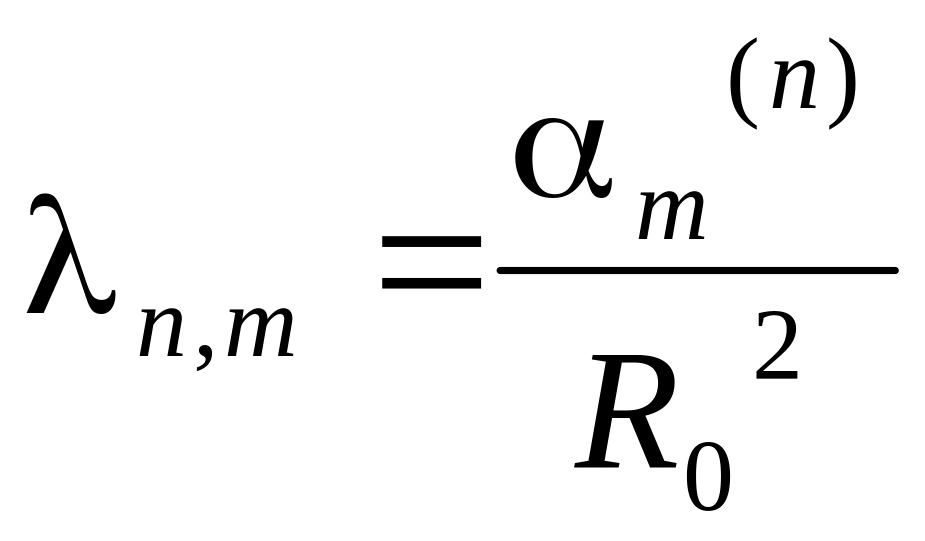
Тогда решение:
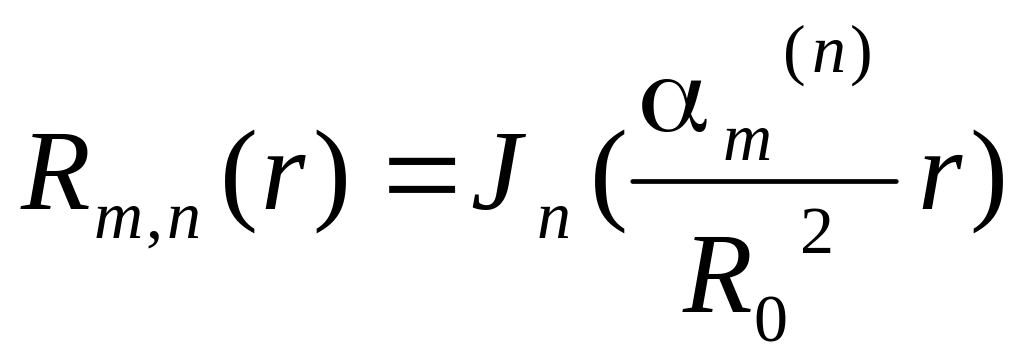
Собственные функции уравнения:
![]() имеют вид
имеют вид
![]()
Тогда решение исходной задачи ищем в форме ряда:
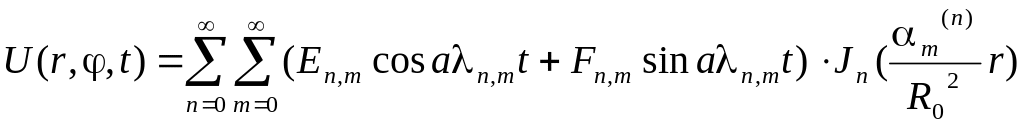 .
.
Коэффициент ряда находим, используя начальные условия и свойство ортогональности
Из
получим, что все
![]() .
.
То
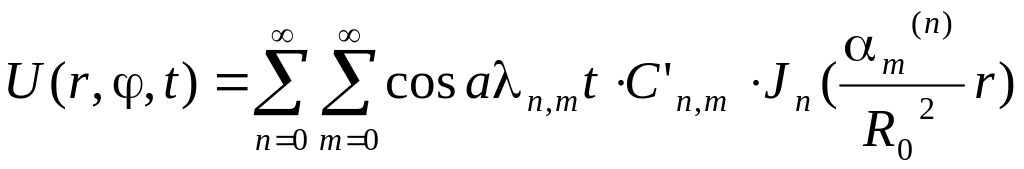 ,
,
где
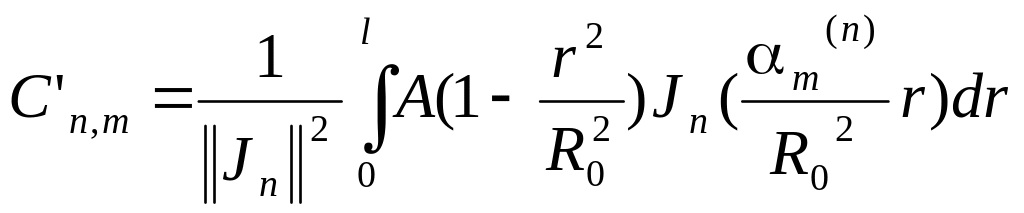
БИЛЕТ 6
Тема 2. Решения задачи Коши для волнового уравнения.
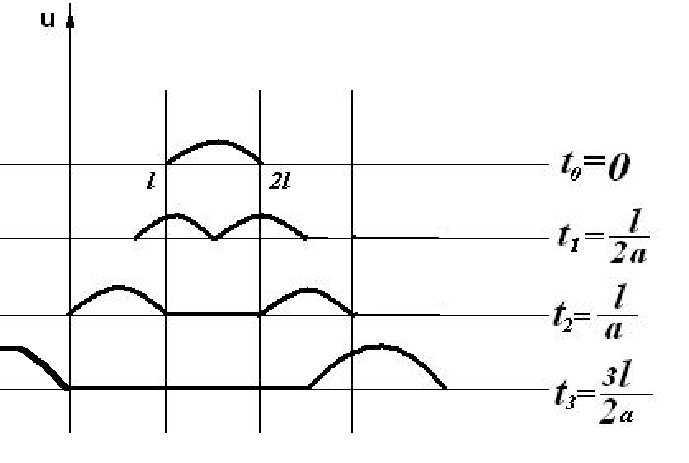
Бесконечная струна возбуждена начальным отклонением

Построить профиль струны для моментов
времени
![]() (k = 1,2,3).
(k = 1,2,3).
Решение
Уравнение малых поперечных колебаний:
![]() .
.
Формула Даламбера:
![]()
где
![]() и
и
![]()
Получаем:
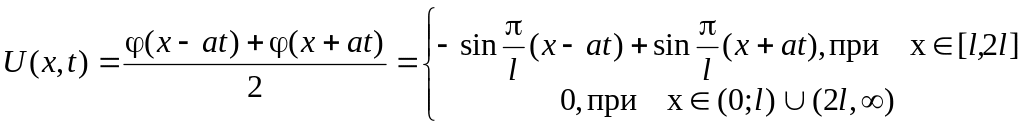
Решение есть суперпозиция 2х волн: прямой и обратной.