
- •Тема 1. Задачи, приводящие к уравнениям различных типов.
- •Тема 3. Метод разделения переменных для решения краевых задач.
- •Тема 1. Задачи, приводящие к уравнениям различных типов.
- •Тема 3. Метод разделения переменных для решения краевых задач.
- •Тема 1. Задачи, приводящие к уравнениям различных типов.
- •Тема 3. Метод разделения переменных для решения краевых задач.
- •Тема 1. Задачи, приводящие к уравнениям различных типов.
- •Тема 3. Метод разделения переменных для решения краевых задач.
- •Билет №5
- •Тема 1. Задачи, приводящие к уравнениям различных типов.
- •Тема 3. Метод разделения переменных для решения краевых задач.
- •Тема 2. Решения задачи Коши для волнового уравнения.
- •Тема 5. Метод функций Грина решения краевых задач для уравнений эллиптического типа.
- •Тема 1. Задачи, приводящие к уравнениям различных типов.
- •Тема 3. Метод разделения переменных для решения краевых задач.
- •Тема 2. Решения задачи Коши для волнового уравнения.
- •Тема 3. Метод разделения переменных для решения краевых задач.
- •Тема 3. Метод разделения переменных для решения краевых задач.
- •Тема 5. Метод функций Грина решения краевых задач для уравнений эллиптического типа.
- •Тема 1. Задачи, приводящие к уравнениям различных типов.
- •Тема 3. Метод разделения переменных для решения краевых задач.
- •Тема 1. Задачи, приводящие к уравнениям различных типов.
- •Тема 3. Метод разделения переменных для решения краевых задач.
- •Тема 1. Задачи, приводящие к уравнениям различных типов.
- •Тема 3. Метод разделения переменных для решения краевых задач.
- •Тема 1. Задачи, приводящие к уравнениям различных типов.
- •Тема 3. Метод разделения переменных для решения краевых задач.
- •Тема 1. Задачи, приводящие к уравнениям различных типов.
- •Тема 3. Метод разделения переменных для решения краевых задач.
- •Тема 3. Метод разделения переменных для решения краевых задач.
- •Тема 5. Метод функций Грина решения краевых задач для уравнений эллиптического типа.
- •Тема 3. Метод разделения переменных для решения краевых задач.
- •Тема 5. Метод функций Грина решения краевых задач для уравнений эллиптического типа.
- •Тема 1. Задачи, приводящие к уравнениям различных типов.
- •Тема 3. Метод разделения переменных для решения краевых задач.
- •Тема 2. Решения задачи Коши для волнового уравнения.
- •Тема 3. Метод разделения переменных для решения краевых задач.
- •Тема 3. Метод разделения переменных для решения краевых задач.
- •Тема 5. Метод функций Грина решения краевых задач для уравнений эллиптического типа.
- •Тема 1. Задачи, приводящие к уравнениям различных типов.
- •Тема 3. Метод разделения переменных для решения краевых задач.
БИЛЕТ 1
Тема 1. Задачи, приводящие к уравнениям различных типов.
Найти область на плоскости, в которой уравнение (y2+1)uxx-x(uxy+uyy)+y(ux+uy)=0 имеет гиперболический тип.
Решение
Для того, чтобы уравнение гиперболического
типа необходимо, чтобы
![]() Преобразуем наше уравнение:
Преобразуем наше уравнение:
![]() .
.
Найдем
![]() ,
известно что:
,
известно что:![]() ,
в нашем случае:
,
в нашем случае:
![]()
Таким образом:![]()
![]()
Неравенство выполняется, когда
![]() и
и
![]() имеют один знак.
имеют один знак.
В первом случае область ограничена
прямой
![]() а во втором параболой с вершиной в точке
(-4,0). Построим графики этих функций.
а во втором параболой с вершиной в точке
(-4,0). Построим графики этих функций.
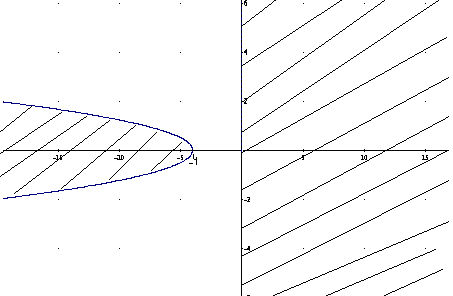
В итоге получим следующую область:
данное уравнение имеет гиперболический
вид в заштрихованных областях, не включая
линий графиков функций
и
![]() .
.
Тема 3. Метод разделения переменных для решения краевых задач.
На концах однородного изотропного стержня длиной l поддерживается нулевая температура. Предполагая, что стенки стержня теплоизолированы от окружающей среды, найти закон распределения температуры в стержне, если известно, что в начальный момент имелось следующее распределение температуры:
![]() , где
U0 = const.
, где
U0 = const.
![]() .
.
Решение
Имеем уравнение теплопроводности:
![]() и краевые условия первого типа. Данную
задачу будем решать методом Фурье.
Решение данной задачи представим в виде
произведения:
и краевые условия первого типа. Данную
задачу будем решать методом Фурье.
Решение данной задачи представим в виде
произведения:
![]() .
.
Подставляем, преобразуя, разделяем переменные:
![]() ,
,
![]() ,
,
Получаем
![]() -
задача Штурма–Лиувилля:
-
задача Штурма–Лиувилля:
Решение этого уравнения в общем виде
![]()
Из начальных и краевых условий:
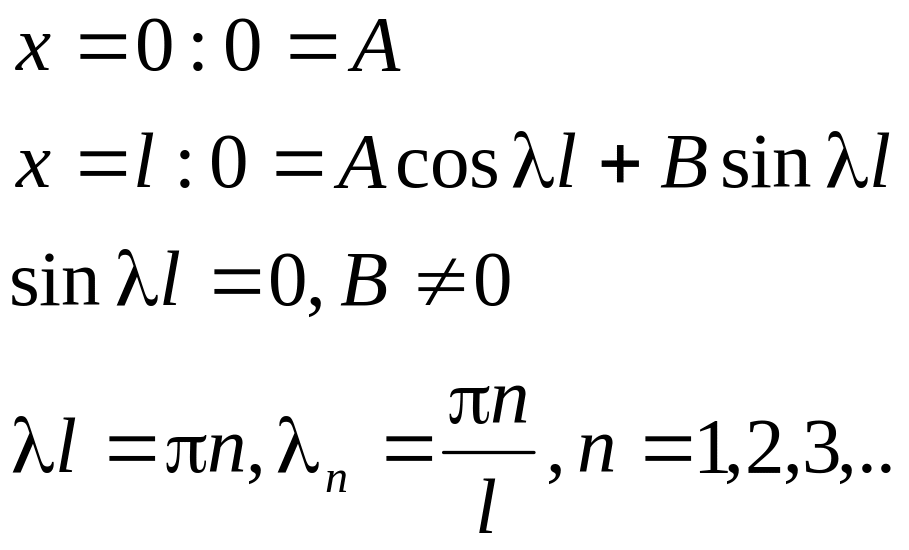
Отсюда собственные функции (с точностью до произвольного постоянного множителя):
![]() .
.
Из второго уравнения:
![]() .
.
Решение этого ДУ:
![]()
Тогда:
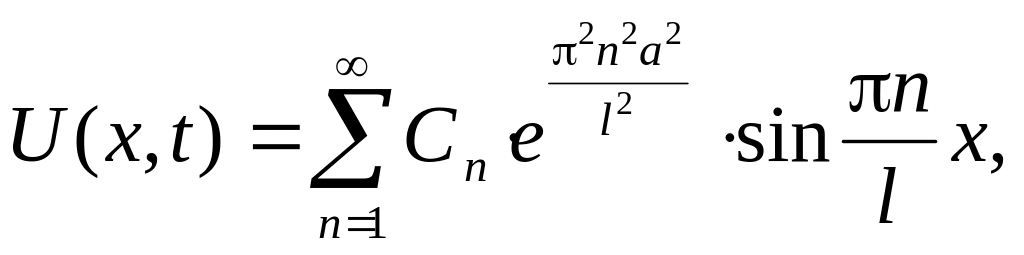
Найдем Cn из начальных условий и принципа ортогональности:
![]()
![]() .
.
Тогда закон распределения температуры
для поставленной задачи запишется в
виде:

БИЛЕТ 2
Тема 1. Задачи, приводящие к уравнениям различных типов.
Найти область на плоскости в которой уравнение x3uxx+2xyuxy+y(1+x)uyy-u=0 имеет эллиптический тип.
Решение
Уравнение имеет эллиптический вид, если
![]() ,
где
,
где
![]()
Для данного уравнения
![]()
![]()
т.к.
![]() всегда, то должно выполнятся
всегда, то должно выполнятся
![]()
Запишем это неравенство как:
![]() Рассмотрим
два случая,
Рассмотрим
два случая,
1) Если
![]() , тогда
, тогда
![]()
2) Если
![]() , тогда
, тогда
![]()
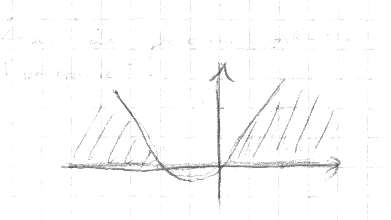
Рис. искомая область.
Тема 3. Метод разделения переменных для решения краевых задач.
Однородная прямоугольная мембрана (![]() ,
,
![]() ),
закрепленная вдоль всего контура,
лежащего в горизонтальной плоскости,
и имеющая в начальный момент форму
),
закрепленная вдоль всего контура,
лежащего в горизонтальной плоскости,
и имеющая в начальный момент форму
![]() ,
начала колебаться с начальной скоростью
,
начала колебаться с начальной скоростью
![]() .
Найти закон свободных колебаний мембраны.
Получить решение в случае
.
Найти закон свободных колебаний мембраны.
Получить решение в случае
![]() ,
если натяжение мембраны Т0
равно ее поверхностной плотности ,
т.е.
,
если натяжение мембраны Т0
равно ее поверхностной плотности ,
т.е.
![]() .
.
Решение
 Предполагая,
что мембрана совершает малые колебания,
запишем уравнения свободных колебаний
мембраны:
Предполагая,
что мембрана совершает малые колебания,
запишем уравнения свободных колебаний
мембраны:
![]() ,
где
,
где
![]() ,
(1)
,
(1)
Имеем 1ю краевую задачу с граничными условиями
![]()
![]() (3)
(3)
![]()
![]() (3)
(3)
Находим решение методом Фурье:
![]() .
(4)
.
(4)
Подставим формулу (4) в уравнение (2),
получим
![]() .
.
Разделив это равенство на
![]() ,
имеем
,
имеем
![]() ,
,
Откуда
![]() ,(5)
,(5)
следовательно,
![]() -
Задача Штурма-Лиувилля
-
Задача Штурма-Лиувилля
Собственные функции (с точностью до произвольного постоянного множителя):
![]() ,
собственные значения
,
собственные значения
![]() ,
n=1,2…
,
n=1,2…
Также из (5) следует
![]() .
(6)
.
(6)
разделим переменные:,
![]() .
.
Откуда
![]()
Решение
![]() собственные значения
собственные значения
![]() , где k=1,2…
, где k=1,2…
Из (6)
![]()
Обозначим
![]() или
или
![]() ;
где
;
где
![]() ,
,
![]() .
(9)
.
(9)
![]()
Каждой паре номеров
![]() ,
,
![]() соответствует свое решение
соответствует свое решение
![]() .
.
Решение этого уравнения:
![]() ,
,
где
![]() и
и
![]() - произвольные постоянные.
- произвольные постоянные.
Подставляя найденные
![]() ,
,
![]() и
и
![]() в (4), получаем все возможные нетривиальные
решения уравнения (1),
в (4), получаем все возможные нетривиальные
решения уравнения (1),
![]() ,
,
Общее решение:
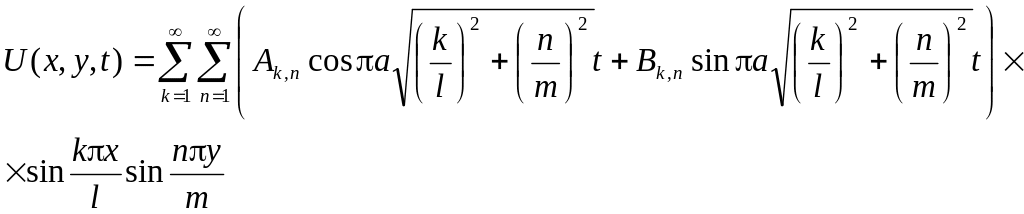 (10)
(10)
Из начальных условий и принципа ортогональности:
![]() и
и
![]() .
.
где , a=1
Из этих равенств заключаем, что все
числа
![]() за исключением коэффициента
за исключением коэффициента
![]() .
А из 2го условия все
.
А из 2го условия все
![]()
Тогда решение
![]() .
.
БИЛЕТ 3
ЗАДАЧИ
